梅冥相. (2011)从旋回的有序叠加形式到层序的识别和划分:层序地层学进展之三* [J]. 古地理学报, 13(1): 37-54
Mei Mingxiang. (2011)From vertical stacking pattern of cycles to discerning and division of sequences: The third advance in sequence stratigraphy[J]. Journal Of Palaeogeography, 13(1): 37-54. DOI:  
Permissions
Copyright©2011, 《古地理学报》编辑部
版权所有.《古地理学报》编辑部
从旋回的有序叠加形式到层序的识别和划分:层序地层学进展之三*
梅冥相
中国地质大学(北京)地质过程与矿产资源国家重点实验室,北京 100083

作者简介：梅冥相,男,1965年生,教授,博士生导师,从事沉积学和地层学研究工作;E-mail: meimingxiang@263.net。

收稿日期:2010-09-10
基金:*国家自然科学基金会资助项目(编号:40472065)和中国石油化工股份有限公司海相前瞻性项目(编号:C0800-07-ZS-164)联合资助
摘要

在 Exxon层序地层学概念体系中,由不整合面及其可以对比的整合面所限定的地层单位被定义为层序,即三级沉积层序;构成三级层序的单元为体系域,体系域由若干准层序和准层序组所组成。基于海岸沉积的层序地层模式,准层序被定义为“由海泛面所限定的层或层组组成的一个相对整合的序列”;作为准层序界面的海泛面被进一步定义为:一个将老地层与新地层分开的面,穿过该面存在一个突然的“水深加深”。因此,从海泛面到准层序,其定义由于不具有普遍性而表现出欠完整性。虽然类似级别的地层单元后来又被 Exxon的科学家修改为“高频层序”,但是,准层序这个欠完整的概念一直被广泛使用着。与层序地层学的 Exxon时代大致同步,或者在更早的时期,地质学家就已经注意到那些由岩层所构成的沉积旋回,以“洛非尔旋回层”为典型代表;这种类似的旋回性沉积记录,后来被进一步定义为“米级旋回”,而且将米级旋回进一步解释为异成因机制控制下的自旋回沉积过程(间断—加积—旋回机制; PAC机制)的产物,这种异成因机制是与米兰柯维奇旋回相关的极地冰盖的消长所造成的海水体积变化,以及由这种数万年至数十万年级别的海水体积变化所产生的高频海平面变化旋回。这些厚度为数厘米至数米的沉积旋回,在长周期三级层序中常常构成有序的叠加形式,这种叠加形式成为研究三级层序内沉积趋势变化的主要标志。再者,对与米兰柯维奇旋回存在成因关联的沉积旋回的研究,成为另一个地层学分支——旋回地层学的主要内容。如果说对 Exxon层序地层学概念体系不协调的研究是第 1个进展、对长周期层序的形成机制的探索为层序地层学的第 2个进展,那么,从旋回的有序叠加形式到层序的识别与划分,不但表现出了旋回地层学和层序地层学的交融,而且也代表了层序地层学的第 3个重要进展。

关键词: 准层序; 沉积旋回; 沉积层序; 层序地层学进展之三
中图分类号:P534 文献标志码:Ａ 文章编号:1671-1505(2011)01-0037-18
From vertical stacking pattern of cycles to discerning and division of sequences: The third advance in sequence stratigraphy
Mei Mingxiang
State Key Laboratory of Geological Processes and Mineral Resources,China University of Geosciences(Beijing),Beijing 100083
Abstract

In the conceptual system of the Exxon sequence stratigraphy,stratal units bounded by unconformities and their correlative conformities are defined as the depositional sequence. The depositional sequence is made up of systems tract,and the systems tract is composed of many parasequences or parasequence sets.In term of the sequence stratigraphic model that is based on the coastal sedimentology,the parasequence can be defined as a relative conformity succession of strata that is bounded by flooding surface; Further,the flooding surface,that is used as the bound surface of parasequence,is defined as a stratigraphic surface that divides the older strata from the young strata through which exists an abrupt rapid deepening of water depth.Thus,there is no universalism for the flooding surface that can be used as the bound surface of parasequence,which leads to the lacking of the integrality for parasequence.The term of the parasequence has subsequently been modified as high-frequency sequence by Exxon scientists,but this term that is lack of integrality has widely been used up to the present.In the same time or the time that is earlier than that of the Exxon age for sequence stratigraphy,the sedimentary cycle that is made up of lithofacies successions had been described by geologists,such as Lofer Cyclothem.This similar type of cyclic sedimentary records has been further defined as meter-scale cycle,and the meter-scale cycle has been interpreted as the product of autocyclic depositional process(the puncatuated aggradational cyclic mechanism;the PAC mechanism)which is controlled by allocyclic mechanism;Further,the allocyclic mechanism was explained as high frequency sea level change that is genetically related to the volume change of sea water due to the increasing and decreasing of ice cap in the polar region resulting from the Milankovitch cycle.These meter-scale cycles with thickness from several centimeters to several meters generally form a vertical stacking pattern in the third-order sequence,and this vertically stacking pattern of meter-scale cycle becomes a main marker to study the change of sedimentary trends within the third-order sequence.Importantly,studies on sedimentary cycles that are genetically related to the Milankovitch cycles are grouped into the main content of other stratigraphic discipline, i.e. the cyclostratigraphy.Therefore,if the study on inconsistence of conceptual system for the Exxon sequence stratigraphic model represents the first advance,while the research on the forming mechanism of those long-term sequences is the second advance in sequence stratigraphy,the study on the discerning and division on the basis of regular vertical stacking patterns of cycles can delegate the third advance in sequence stratigraphy,which is marked by the mingling of both sequence stratigraphy and cyclostratigraphy.

Key words: parasequence; sedimentary cycle; depositional sequence; the third advance in sequence stratigraphy

1977年, Peter Vail和他的来自Exxon公司的同事们, 通过地震剖面展示了由一系列部分被不整合面所限定的单位构成的沉积记录(Vail et al., 1977); 他们遵循Sloss(1963)的工作, 将这种单位定义为“ 沉积层序” , 即“ 由不整合面及其可以对比的整合面所限定” 的单位(Mitchum et al., 1977), 并提出了新定义“ 层序” 形成过程的海平面变化旋回解释, 从而代表了一个具有较为完整的概念体系和可操作的工作方法体系的“ 层序地层学” 分支的诞生。这些概念体系和方法学较为系统地出现在一个分水岭式的出版物中, 即AAPG地震地层学26号专辑(Payton, 1977); 另一个分水岭式的出版物, 即SEPM Special Publication 42(Wilgus et al., 1988)的出版, 意味着层序地层学的概念体系和方法学进入了成熟阶段。因此, 可以将1977年至1988年称为层序地层学的Exxon时代。在基于海岸沉积的Exxon层序地层学模式中, 一个层序可以根据一系列的层序地层界面如海侵面和最大海泛面而进一步划分为体系域, 一个体系域则被定义为由若干成因相关的准层序和准层序组所构成, 准层序则被定义为由海泛面所限定的层或层组组成的一个相对整合的序列(Van Wagoner et al., 1988)。这样, 一个较为完整的层序地层学概念框架即“ 层序— 体系域— 准层序” 就产生了, 这个概念框架一致被广泛使用到今天(Catuneanu et al., 2009; 吴因业等, 2010)。

与层序地层学的Exxon时代大致同步, 或者在更早的时期, 地质学家们就已经注意到那些由相关岩层所构成的沉积旋回, 以“ 洛非尔旋回层(Lofer cyclothem; Fischer, 1964)” 为典型代表。地层中这种类似的旋回性沉积记录, 尽管从18世纪晚期的Gilbert时代就已经被注意到, 但由于其成因机制得不到合理的解释而被忽视, 一直到1978年Reading在其主编的《沉积环境与相》一书中还告诫人们:“ 旋回太主观, 会造成沉积学家和地质学家对地层记录本身的物质特性及其规律性的简单认识…” ; 当然, 这种认识在1996修订出版该书的第3版时已经完全改变(Reading, 1996), 在该书的第2章即“ 沉积岩石记录的控制” 中专门讨论了“ 米兰科维奇过程和轨道效应” 。随着对地层堆积作用的间断— 加积旋回机制(PAC机制)的提出(Goodwin and Anderson, 1985)以及“ 米级旋回” (Anderson and Goodwin, 1990)概念的出现, 而且将米级旋回进一步解释为异成因机制控制下的自旋回沉积过程的产物, 不但意味着地层学的另一个分支— — 旋回地层学进入了地层学实践的主流, 而且沉积旋回的研究已经不自觉地成为“ 准层序” 的延伸和拓展(Goldhammer et al., 1990; Osleger and Read, 1991a, 1991b; Krapez, 1993; Mei et al., 2000; 梅冥相和高金汉, 2005; Strasser et al., 2006; Spence and Tucker, 2007; 陈留勤, 2008; Catuneanu et al., 2009), 形成了今天层序地层学与旋回地层学相互交融的局面。从以岩相序列所组成的旋回的识别及其叠加形式的研究, 以及这些叠加形式所反映出的地层记录中的“ 米兰科维旋回性质” 的研究, 不但为层序的识别提供了一个研究沉积趋势变化的基础(Goldhammer et al., 1990; Osleger and Read, 1991a, 1991b; Fischer and Bottjer, 1991; Schwarzacher, 1993; Mei et al., 2000, 2001a, 2001b; 梅冥相和高金汉, 2005; Strasser et al., 2006; Spence and Tucker, 2007; Catuneanu et al., 2009), 而且还可以对地层堆积作用过程所经历的时间进行估算(江大勇等, 1999; 郝维成等, 2000; Mei et al., 2000, 2001a, 2001b; 龚一鸣等, 2004), 并对三级层序形成的海平面变化幅度进行半定量模拟和估算(Osleger and Read, 1991a, 1991b; Schwarzacher, 1993; Mei et al., 2000, 2001a, 2001b; 梅冥相和高金汉, 2005; Strasser et al., 2006; Spence and Tucker, 2007), 从而提供一些有趣而重要的信息。因此, 如果说对Exxon层序地层学概念体系的研究是第1个进展、对长周期层序形成机制的探索理解为层序地层学的第2个进展(梅冥相, 2010a, 2010b), 那么, 从旋回的识别到旋回的有序叠加形式对层序的识别与划分, 不但表现出了旋回地层学和层序地层学的交融, 而且也代表了层序地层学的第3个重要进展。

1 准层序

在Exxon层序地层学概念体系中, 一个层序由不整合面及其可以对比的整合面所限定, 一个层序内部可以通过两个层序地层界面即最大海泛面和初始海泛面(或海侵面)进一步划分为体系域, 而体系域则由若干准层序和准层序组所构成。基于海岸沉积的层序地层模式, Van Wagoner等(1988)通过一个界面定义了准层序— — “ 由海泛面所限定的层或层组构成的一个相对整合的序列” 。作为准层序界面的海泛面, Van Wagoner 等(1988)将其定义为:“ 一个将老地层与新地层分开的面, 穿过该面存在一个突然的水深增加” 。这个准层序的定义主要基于海岸沉积模式, 从海泛面的概念到准层序的概念, 其定义均不具有普遍性而造成概念的欠完整性。其后将类似于准层序的地层单元重新命名为“ 高频层序” , 对这种欠完整性进行了一定程度的修正(Van Wagoner et al., 1990; Mitchum and Van Wagoner, 1991)。

穿过一个海泛面, 沉积物具有沉积环境突然加深的基本属性(Van Wagoner et al., 1988), 对于滨岸— 陆棚沉积体系来说确实如此; 但是在潮坪沉积体系中, 所谓的“ 海泛面” 位置常常是一个瞬时性的暴露间断面。如果在滨岸— 陆棚沉积体系中沉积环境水体突然加深代表了海泛面的基本属性, 那么, 潮坪沉积体系中的那些瞬时暴露间断面(Mei et al., 2000, 2001a, 2001b; 梅冥相和高金汉, 2005; Spence and Tucker, 2007)就应该定义为“ 海退面” 。因此, 将海泛面与准层序严格对等起来就造成了准层序定义的欠完整性, 在纯粹的河流以及深水体系中 “ 海泛面” 的概念失去意义, 所以准层序这个术语后来也被Exxon科学家们质疑(Posamentier and Allen, 1999)。Catuneanu 等(2009)认识到, 在海岸和浅水体系中才具有制图性的准层序, 在层序(层序包括了穿过一个沉积盆地的沉积体系的完整排列)和准层序(在地理范畴内只是限定于一个沉积盆地的海岸和浅水部分)的概念层次之间标定了一个差异。准层序的形成可以由自旋回因素控制, 例如在三角洲体系中的辫状体的转换和废弃, 或者由异旋回机制控制。在后一种情况下, 准层序可能是在米兰科维奇频率带中基准面旋回的产物, 因此它们可以被看成在其所发育的地区内较小级别的层序(Krapez, 1993; Strasser et al., 2006), 就像王鸿祯和史晓颖(1998)所称的“ 小层序” 那样。Catuneanu 等(2009)还进一步建议, “ 准层序” 这个术语还可以扩展为包括具有区域意义的米级旋回, 不管它们是否由海泛面所限定(Spence and Tucker, 2007)。Catuneanu等(2009)所提及的“ 米级旋回” , 又涉及到另一个地层学分支— — 旋回地层学的概念体系(陆元法和李文汉, 1989; Fischer and Bottjer, 1991; Schwarzacher, 1993; 覃建雄等, 1995; 吴智勇和姜衍文, 1996; 徐道一, 2005; 徐道一等, 2006; Strasser et al., 2006)。

2 旋回

“ 旋回” 这一术语, 就像“ 层序” 一样, 在不同的地质学科中具有不同的涵义, 如构造旋回、火山旋回等。沉积旋回是指在一个沉积序列中规则地重复发生的、不同组构及岩相的组合(Schwarzacher, 1993)。旋回的研究来自于早期韵律性沉积作用的概念, Gilbert在1895年就指出了一定的韵律层理形式可能记录了敏感的地球轨道韵律的反应, 这些信号可能提供了地质年代学的基础, Gilbert的设想成为当时颇为紧迫的课题。尽管Schwarzacher(1975)在《沉积模型与定量地层学》一书中, 强调了桑德尔法则(空间上的旋回性代表了时间上的旋回性, 但地层记录中旋回性的缺失并不指示时间旋回性的缺失; Sander, 1936)的重要性, 较为完整地论述了“ 沉积旋回” 与米兰柯维奇旋回之间可能的成因关联, 以及Fischer(1964)对“ 洛非尔旋回层” 的研究和解释以及他对Gilbert式层理韵律的研究(Fischer, 1980), 但是, 就像Reading在1978年还认为“ 旋回” 一词太主观一样, 沉积旋回的地质学涵义及其重要性在层序地层学的Exxon模式于1977年出现之前似乎只是得到少数学者如Schwarzacher等的坚持和强调。

层序地层学的兴起及对层序形成的海平面变化假说的广泛接受, 以及Berger(1978)和其他学者的工作, 增强了地质学家洞察轨道效应及其所产生的气候变化的能力(Authur et al., 1984), 促使沉积学家更加关注和研究沉积旋回, 并运用米兰科维奇旋回(Milankovitch, 1941)来解释和分析Gilbert式层理韵律所代表的沉积旋回。尽管对这种解释还存在不同的认识和看法(Wilkinson et al., 1996, 1997a, 1997b, 1999), 一个可以进入地层学实践主流的旋回地层学已经逐渐形成(Schwarzacher, 1993; Hinnov, 2000; Strasser et al., 2006; Hinnov and Ogg, 2007)。如果说Exxon的科学家根据准层序的叠加形式推断出地层堆积作用的3种形式(即进积作用、加积作用和退积作用形式; Vail et al., 1977; Van Wagoner et al., 1988, 1990; Mitchum and Van Wagoner, 1991)是对地层堆积作用过程之中相迁移的重要总结, 那么地层堆积作用的“ 间断— 加积— 旋回” 机制(Goodwin and Anderson, 1985)的提出又从本质上揭开了其作用过程复杂性的面纱, 由此而产生的“ 米级旋回” 的概念又成为层序地层学概念体系中欠完整的“ 准层序” 的良好补充(Mei et al., 2000, 2001a, 2001b; 梅冥相和高金汉, 2005; 陈留勤, 2008)。

“ 米级旋回” 的概念出自于地层堆积作用的“ 间断— 加积— 旋回” 模式(Goodwin and Anderson, 1985), 被定义为“ 露头上能直接识别的数厘米至数米厚、成因相关的岩相单元所构成的地层序列” (Anderson and Goodwin, 1990), 这种厚度级别的旋回性沉积记录运用米兰科维奇旋回机制所产生的冰川型海平面变化得到了合理的解释, 即异成因机制控制下的旋回过程的产物(Fischer and Bottjer, 1991; Schwarzacher, 1993; Mei et al., 2000; Strasser et al., 2006; Spence and Tucker, 2007)。沉积旋回类似于沉积相模式中的“ 相序” 模式(Reading, 1978, 1996; Miall, 1984, 1990; Walker, 1984; 冯增昭, 1989), 只不过以前人们更加关注其自成因机制的研究。

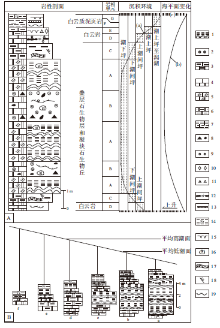
图1 米级旋回的总体相序模式（A— 缓坡型台地中米级旋回的环境变化谱系:a为环潮坪型; b为潮下型; c为L-M型; B— 镶嵌陆架型台地中米级旋回的环境变化谱系, a至c的含义同图A, d代表深水非对称型米级旋回; C— 碳酸盐岩米级旋回的总体模式, 两种组构不同的相序模式; D— 碎屑岩米级 旋回的总体模式, 向上变细的潮汐动力型以及向上变粗的波浪动力型）Fig.1 General models of lithofacies successions for meter-scale cycle

基于前人的研究成果, 碳酸盐岩米级旋回大致可以归为4大类(图 1所示; Mei et al., 2000): (1)环潮坪型碳酸盐岩米级旋回(图 1-A和1-B中a所示; 图1-C), 早期由Read(1985)以潮坪碳酸盐相序模式的形式进行了描述和总结, 旋回顶部明显的白云石化作用以及喀斯特化作用代表了该类型旋回的界面以瞬时暴露间断面为特征, 形成一个沉积环境总体向上变浅、岩层向上变薄、颗粒向上变细的“ 正粒序相序序列” ; (2)潮下型碳酸盐岩米级旋回, 最早由Osleger(1991)提出并系统总结, 这种类型的旋回不具暴露作用特征, 为一个叠加在加深间断面(类似于海泛面)之上的变浅序列(图 1-A和1-B中b所示; 图1-C), 形成一个沉积环境总体向上变浅、岩层向上变厚、颗粒向上变粗的“ 反粒序相序序列” ; (3)L-M型碳酸盐岩米级旋回(图 1-A和1-B中c所示), 是研究的最早的一种沉积旋回类型(Authur et al., 1984; Schwarzacher, 1975, 1993), 由泥灰岩(Marl)和灰岩(Limestone)构成的一种简单韵律形式而得名, 形成在斜坡至陆棚背景之中, 其基本特征类似于潮下型; (4)深水非对称型碳酸盐岩米级旋回(1-B中d所示), 这种类型的碳酸盐岩米级旋回常常发育在镶嵌陆架型台地边缘的上斜坡环境之中, 最早由Masetti等(1991)提出并系统描述和研究, 其总体特征类似于潮下型, 常常是一个在L-M型或潮下型旋回的顶部发育塌积角砾灰岩层的岩相序列。因此, 碳酸盐岩米级旋回总体上可以归为两大类(图 1-C):以正粒序岩相序列为特征的环潮坪型和以反粒序岩相序列为特征的潮下型。

碎屑岩米级旋回常常发育在滨面至滨线的浅水背景之中, 基于海岸沉积的层序地层学模式, Mitchum 和 Van Wagoner(1991)主要描述了从陆棚相泥岩到滨岸相砂岩的类型, 并将其定义为“ 高频层序” , 因为这种类型的米级旋回总是以瞬时加深间断面— — 层序地层学中的“ 海泛面” 作为分界面; 在潮坪沉积体系之中, 还发育有从潮下坪砂岩到潮上坪泥岩的正粒序岩相序列的米级旋回, 这种类型的米级旋回不是以“ 海泛面” 为分界面, 而是以海退面— — 瞬时暴露间断面为分界面。类似碳酸盐岩中的潮下型和环潮坪型米级旋回, 碎屑岩中的两种类型可总结为波浪动力型和潮汐动力型米级旋回(图 1-D)(Mei et al., 2000)。需要强调的是, 米级旋回多发育在浅水背景之中, 数万年至数十万年级别的、多为数米幅度的海平面变化在深水背景之中难以留下明显的沉积记录, 这就是“ 桑德尔法则” 的基本含义— — “ 地层记录中旋回性的缺失并不代表时间旋回性的缺失” 。

对于米级旋回的叠加形式还可以根据米兰科维奇旋回频带所赋予的“ 米兰科维奇旋回属性” 来推断米级旋回的大致形成时限, 从另一个角度估计出地层堆积作用的时间。根据米兰科维奇信号对泥盆纪牙形石带分布时限的研究是这方面的典型实例(江大勇等, 1999; 郝维成等, 2000; 龚一鸣等, 2004)。对那些具有数个岩相单元或具有近似对称相序组构所构成的米级旋回, 还赋予其特定的名称来表现其重要性, 如“ 洛非尔旋回层” (Fischer, 1964)、北美石炭系中的海相含煤的“ 堪萨斯型旋回层” 和非海相的“ 阿帕拉契亚型旋回层” 以及过渡性质的“ 伊利诺斯型旋回层” 所组成的“ 宾夕法尼亚旋回层” (Klein and Willard, 1989)、“ 雾迷山旋回层” (Wumishan cyclothem; Mei et al., 2001a, 2001b)等。

从早期只是由不整合面所限定的层序概念, 到后来将层序定义为不整合面及其可以对比的整合面所限定的地层序列的变化, 实际上就意味着典型的层序界面除了包括代表地层明显间断的平行不连续面以及代表地层明显不协调接触关系的角度不整合面(张守信, 2006), 还包括传统上被认为是整合序列的地层的进一步层序划分和识别。层序地层学发展到今天, 似乎对角度不整合面、平行不连续面和那些沉积间断面等反映地层不连续和不协调关系的界面还重视不够, 不胜枚举的研究实例所表现出的层序划分实际上是把那些沉积间断面作为层序界面的划分, 而这些沉积间断面实际上就是沉积旋回的界面, 以米级旋回为代表的沉积旋回的形成机制— — “ 间断— 加积— 旋回” 模式(PAC模式; Goodwin and Anderson, 1985; Anderson and Goodwin 1990; Mei et al., 2000; Spence and Tucker, 2007)就充分表明了地层间断存在不同的层次。从旋回的识别到层序的划分, 则导致了层序地层学研究的一些重要变化, 主要是在传统上认为是整合序列的地层中进行层序划分。

3 从旋回到层序

层序地层学与旋回地层学的交融 以“ 米级旋回” 为代表的沉积旋回(图 1), 由于反映了地层记录中米兰科维奇旋回的信息而成为旋回地层学的基本单位; 对沉积旋回的研究, 已经提供了关于地层堆积作用的许多重要信息, 旋回地层学总体上被限定为对与米兰柯维奇旋回相关的沉积旋回的研究(Fischer and Bottjer, 1991; Schwarzacher, 1993; Strasser et al., 2006), 这种限定似乎不太符合完整的科学理念。从旋回的识别以及旋回的有序叠加形式去进行层序划分又代表了今天层序地层学的一个重要进展和变化(Osleger, 1991; Osleger and Read, 1991a, 1991b; Mei et al., 2000, 2001a, 2001b; Spence and Tucker, 2007), 主要表现在:(1)类似于准层序组成准层序组的概念(Van Wagoner et al., 1990; Mitchum and Van Wagoner, 1991), 沉积旋回由4个构成一组可能反映了长偏心率和短偏心率旋回的叠加, 诸如此类的现象可以用来推断单个旋回的形成时限, 从地层堆积作用本身得出一个时间的估计; (2)旋回厚度的变化被假定为代表沉积物可容纳空间的变化, 运用一种半定量的费希尔图解法来进一步模拟三级海平面变化旋回的幅度, 为层序的划分提供更加确切的依据; (3)若干实例的描述和研究表明, 如Goldhammer等(1990)对阿尔卑斯山三叠系“ 洛非尔旋回层” 的叠加形式的研究、Osleger和Read(1991a, 1991b)对北美寒武系、Mei等(2001a, 2001b)对中元古界雾迷山组巨厚的碳酸盐沉积序列的研究, 总体上证实了偏心率旋回(短偏心率旋回的周期为10万年、长偏心率旋回的周期为40万年; Milankovitch, 1941)在漫长的地质历史时期中的总体稳定性(Berger et al., 1992; Lasker, 1999), 这种较为稳定的旋回周期常常在地层记录中形成4个旋回构成一组的1:4叠加形式, 从而赋予每一个旋回10万年左右的准周期性, 这种现象还被誉为地质计时的“ 天文钟摆” (汪品先, 2006), 对类似现象的研究被称为“ 天文地层学” (徐道一, 2005; 徐道一等, 2006)。北京西山寒武系张夏组中潮下型碳酸盐岩米级旋回的叠加形式所代表的一个鲕粒滩序列组成的三级层序, 以及天津蓟县厚度超过3000m的中元古界雾迷山组中特别的“ 雾迷山旋回” 的叠加形式, 可以作为岩相序列构成的“ 米级旋回” 、沉积相序列构成的三级层序的典型实例。

3.1 北京西山寒武系张夏组的相序特征及其旋回性

北京西山的寒武系张夏组, 地层时代大致相当于下寒武统鼓山阶(彭善池和Bobcock, 2005; 彭善池, 2006, 2008; 章森桂等, 2009)。以发育鲕粒灰岩为特征的张夏组(图 2-A)(冯增昭等, 1990; 冯增昭, 1994; 王英华等, 1994), 还发育深水生物丘灰岩(图 2-B), 中至深缓坡相泥质条带泥晶灰岩中常常夹有风暴粒屑灰岩透镜体和透镜层(图 2-C)以及陆棚相钙质泥岩(图 2-D)。

鲕粒灰岩层和泥晶灰岩层常常与深缓坡相泥灰岩或陆棚相钙质泥岩组成以瞬时加深间断面为界面的潮下型和L-M型米级旋回(图1, 图2-B, 图3-C), 这些米级旋回的有序叠加形式所反映的沉积趋势成为划分长周期三级层序和四级亚层序的基础(图 4), 最为有趣的是, 旋回的界面(图 2-B, 图3-C)与四级亚层序的界面(图 3-B)乃至层序的界面(图 3-A)存在明显的相似性, 充分表明了层序地层学划分是在传统地层学意义上的“ 整合序列” 中进行的。旋回的岩相序列组构特征与三级层序或四级亚层序的沉积相序列组构也具有相似性, 从而表明了“ 旋回含旋回” (Miall, 1984, 1990)的特点, 也表明了旋回性沉积记录明显具有层次性。

从陆棚相钙质泥岩到块状颗粒滩相鲕粒灰岩, 组成一个总体向上变浅的沉积相序列, 该序列组成一个三级层序; 其内部还可以进一步划分为3个次级的沉积相序列, 这3个序列组成3个四级亚层序(图 4; 梅冥相和梅仕龙, 1997)。如图4所示, 构成张夏组三级层序以及四级亚层序的界面类似于Exxon层序地层学模式中的“ 海泛面” , 这些界面本质上与每一个潮下型米级旋回的界面没有太大的区别, 均表现为一个向上突然加深的沉积间断面, 只是厚度上存在一些差异, 所以, 三级层序和四级亚层序均构成较为典型的淹没不整合型层序(Schlager, 1989, 1998, 1999; Gó mez and Fern-ndez-Ló pez, 1994; 梅冥相, 1996)。因此, 沉积旋回及其有序叠加形式就成为张夏组长周期三级层序和四级亚层序划分与识别的基础, 从而成为旋回地层学与层序地层学交融的典型实例。从岩相序列到沉积旋回的识别, 根据沉积旋回的有序叠加形式所反映的沉积相趋势变化进行长周期三级层序和四级亚层序的识别与划分, 不但是对层序地层学中欠完整的“ 准层序” 的良好补充, 而且是在地层年代格架内观察沉积趋势的最好方法(Catuneanu, 2006; Catuneanu et al., 2009)。要特别指出的是, 张夏组中潮下型(图 3-C)和L-M型米级旋回(图 2-B)常常每4个组成1个更大级别的旋回, 类似于北美的寒武系(Osleger, 1991; Osleger and Read, 1991a, 1991b), 该现象可能进一步代表了叠加在长偏心率旋回之上的短偏心率旋回所造成的高频率海平面变化旋回, 从而反映了地层记录中的米兰科维奇旋回信号。在北京西山下苇甸剖面张夏组中识别出80个旋回, 假定每一个旋回的形成时限为10万年, 则推断出张夏组的形成时限为8Ma左右(梅冥相和梅仕龙, 1997)。但是,

图2 北京西山下苇甸剖面寒武系张夏组主要岩性（A— 鲕粒灰岩, 张夏组上部28层; B— 发育在陆棚相钙质泥岩中的生物丘灰岩、钙质泥岩和泥晶灰岩组成的L-M型米级旋回(箭头所示), 张夏组底部21层中部; C— 中缓坡相泥质条带泥晶灰岩中的风暴竹叶状砾屑灰岩, 张夏组下部22层中部; D— 陆棚相钙质 泥岩, 张夏组底部21层下部; 这些层号的地层位置见图4）Fig.2 Photos showing main lithology of the Cambrian Zhangxia Formation at Xiaweidian section in Western Hill of Beijing

这个数据大致是张夏组所主要分布的鼓山阶年龄值(506.5~503Ma; 彭善池和Bobcock, 2005; 彭善池, 2006, 2008; 章森桂等, 2009)的2倍有余, 有可能图2-B所示的那些L-M型旋回的形成不完全是米兰科维奇旋回所产生的高频率海平面变化旋回的产物, 而纯粹是自成因机制的产物, 因此代表了失真的米兰科维奇旋回信号(Wilkinson et al., 1996, 1997a, 1997b, 1999)。

图3 北京西山下苇甸剖面寒武系张夏组中的旋回和层序的界面（A— 张夏组顶部的层序界面(箭头所指; 28层之顶), 被崮山组底部深缓坡至陆棚相夹条带状灰岩透镜体的钙质泥岩直接覆盖而显示出淹没不整合型层序界面的特征; B— 张夏组第1个四级亚层序的顶界面(箭头所指; 21层之顶), 浅缓坡相含鲕粒泥粒灰岩直接被陆棚相钙质泥岩覆盖, 也表现为突然加深的淹没不整合型界面的特点; C— 张夏组上部(27层中部)薄层深缓坡相 泥灰岩或陆棚相钙质泥岩与块状鲕粒灰岩构成的潮下型米级旋回(粗箭头所示); 各层的地层位置见图4）Fig.3 Photos showing boundaries of cycles and sequences of the Cambrian Zhangxia Formation at Xiaweidian section in Western Hill of Beijing

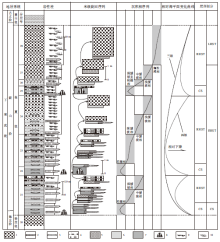
图4 北京西山下苇甸剖面寒武系张夏组沉积相序列及层序地层划分（1— 鲕粒滩相灰岩; 2— 被解释为风暴沉积的竹叶状砾屑灰岩; 3— 泥晶灰岩透镜体; 4— 中缓坡相含鲕粒泥粒灰岩; 5— 中缓坡相泥质条带泥晶灰岩; 6— 深缓坡相泥质条带泥灰岩; 7— 陆棚相钙质泥岩; 8— 生物丘灰岩; 9— 冲刷面; 10— 交错层理; CS代表凝缩段, RHST为构成四级亚 层序的相对高水位体系域; EHST代表三级层序的早期高水位体系域, LHST代表三级层序的晚期高水位体系域）Fig.4 Sequence stratigraphic divisions and sedimentary successions of the Cambrian Zhangxia Formation at Xiaweidian section in Western Hill of Beijing

3.2 天津蓟县剖面中元古界雾迷山旋回以及雾迷山组的层序划分

天津蓟县剖面的雾迷山组, 为一套厚度达3300m的、以叠层石白云岩(图 5)为主的潮坪相碳酸盐岩地层; 其中潮下相叠层石生物层、凝块石生物丘与潮坪相泥晶白云岩、潟湖相白云质泥页岩一起构成若干个环潮坪型碳酸盐岩米级旋回(Read, 1985; Mei et al., 2000; Spence and Tucker, 2007), 这些米级旋回由于具有一个近似对称的岩相序列而区别于一般的环潮坪型碳酸盐岩米级旋回, 所以被特别命名为 “ 雾迷山旋回层” (图 6-A; Mei et al., 2001a, 2001b; 梅冥相等, 2008)。

图5 蓟县剖面中元古界雾迷山组叠层石生物层和凝块石生物丘构成的潮下相单元（A— 假裸枝叠层石, 沉积学意义上的胶结物相叠层石, 三级层序DS9下部; B— 锥状叠层石, 为典型的泥晶相叠层石, 三级层序DS19下部; C— 发育最多但不具有特殊形态而进行命名的波状和微波状叠层石, 也属于泥晶相叠层石, 三级层序DS9下部; D— 凝块石生物丘白云岩, 常常与叠层石生物层白云岩互层产出, 三级层序DS9下部）Fig.5 Photos showing subtidal lithofacies made up of stromatolitic biostrome and thrombolitic bioherm in the Mesoproterozoic Wumishan Formation at Jixian section

构成“ 雾迷山旋回层” 的岩相单元(图 6-A; Mei et al., 2001a, 2001b)包括:A, 潮下坪叠层石生物层白云质灰岩及灰质白云岩; B, 潮下坪凝块石生物丘白云岩; C, 下潮间坪硅化微生物席白云岩; D, 上潮间坪含砂泥晶白云岩; E, 潮上坪泥质白云岩; F, 潟湖相白云质泥页岩; G, 古土壤层。多数旋回层以单元D作为基底, 少数旋回层还可以以单元E作为基底, 而单元A和单元B的不规则交互则构成旋回层的主体部分, 最终构成一个近似对称的岩相序列。因此, “ 雾迷山旋回层” 代表了雾迷山组叠层石碳酸盐岩沉积序列的基本地层结构。要特别指出的是, 单元B是该叠层石碳酸盐岩沉积序列中发育的一种特殊的“ 非叠层石碳酸盐岩” , 赵震(1992)曾经在该岩相单元中发现并定义了核形石与凝块石的过渡类型颗粒, 称为“ 核形石雏形— — 弥散粒” ; 单元F, 还发育特别的黏土矿物组合(黄学光等, 1996)。根据上述特征, 可以总结出“ 雾迷山旋回层” 的基本相序模式, 而且岩相单元D(含砂泥晶白云岩)多作为旋回层的基底以及向上变浅的上部岩相单元, 所以那些相序较为完整的旋回层具有一个近似对称的岩相序列(图 6-A)。7种岩相单元要组成厚度为3000余米的地层序列, 意味着每一种岩相单元将重复性地产出和发育, 意味着地层记录中发育各种级别的旋回。如果图3和图4所示的寒武系张夏组中的潮下型米级旋回均以瞬时加深淹没间

图6 “ 雾迷山旋回层” 的相序模式(A)及其环境变化谱系(B)（图(A)中, “ A” 至“ G” 代表不同的岩相单元, 说明见正文; (a)为水深变化曲线, (b)代表高频率六级海平面变化曲线, (c)指旋回层的暴露间断面。图(B)中, “ a” 至“ f” 表示随着沉积环境水体的逐渐变浅, “ 雾迷山旋回层” 的相序组构将发生有规律的变化, 从而形成一个环境变化谱系; 图例符号分别是:1叠层石; 2核形石; 3硅化微生物席白云岩; 4白云质灰岩; 5叠层石白云岩; 6砂泥质白云岩; 7白云质泥页岩; 8凝块石; 9硅化鲕粒; 10石盐假晶; 11喀斯特角砾; 12硅结壳; 13钙结壳; 14古土壤层; 15泥裂; 16燧石结核; 17板刺状角砾; 18交错层理; 19冲刷面）Fig.6 A general model for the Wumishan cyclothems(A)and their general environmental spectrum(B)

断面作为分界面, 雾迷山旋回层则以瞬时暴露间断面为其分界面(图 7); 从传统的地层学意义上讲, 这些瞬时暴露间断面达不到平行不连续面, 更达不到角度不整合面之类的地层面所反映出的地层间断, 因此, 雾迷山组本身是一个传统地层学意义上的整合序列。在这种年代地层分辨率较低的前寒武纪地层之中进行层序划分时, 从岩相单元的识别到沉积旋回的归类, 根据沉积旋回的有序叠加形式所反映出的沉积趋势来进行层序划分总体上还是一种可行的办法(Catuneanu et al., 2005, 2009; Catuneanu, 2006), 但是难以区分出类型1或类型2界面, 从而表明不一定要套用Exxon层序地层学模式。

最为重要的是, 在三级海平面上升所造成的沉积环境水体加深过程中, 组成“ 雾迷山旋回层” 中部的岩相单元A(叠层石生物层)和单元B(凝块石生物丘)较为发育, 以近似对称的岩相序列为特征; 反之, 在三级海平面下降所造成的沉积环境水体变浅过程中, 即在强迫型海退过程中(Hunt and Tucker, 1992), 单元A和B不发育, 旋回层由近似对称的岩相序列变为不对称的向上变浅序列; 结果, 在厚度巨大的雾迷山组叠层石碳酸盐岩沉积序列中, “ 雾迷山旋回层” 形成一个有序的环境变化谱系(图 6-B)。也正是根据“ 雾迷山旋回层” 在长周期三级层序中的有序垂直叠加形式(以图8的DS10和DS20为代表), 可以把雾迷山组划分为26个三级层序, 并进一步归为6个二级层序(或三级层序组), 组成一个复杂有序的复合海平面变化旋回层序(图 8; Goldhammer et al., 1990)。该复合海平面变化旋回层序表明, 在雾迷山组中可以识别出从二级层序到六级旋回的各种尺度或级别的旋回性地层记录, 雾迷山旋回层反应的是岩相尺度的旋回, 由这些旋回层的有序叠加所构成的三级层序则反映了沉积相尺度的旋回性。

图7 蓟县剖面中元古界雾迷山组中旋回与层序的界面（A— 一个近似对称的岩相序列构成的“ 雾迷山旋回层” , 虚线箭头所指处为旋回界面, 三级层序DS8的中部; B— 一个三级层序上部的不对称相序组成的旋回层, 如“ DEFG” 序列, 图8所示的DS8的顶界面; C— 由古土壤层(G单元)所代表的旋回界面, 三级层序DS8的中部; 图中A至G代表不同的岩相单元, 详见正文所述, 它们所构成的旋回层类型见图6）Fig.7 Photos showing boundaries of cycles and sequences for the Mesoproterozoic Wumishan Formation at Jixian section

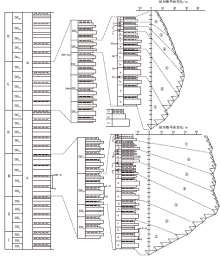图8 蓟县剖面中元古界雾迷山组复合海平面变化层序（雾迷山组可以划分为26个三级层序(DS1至DS26), 并进一步归为6个二级层序(Ⅰ 至Ⅵ )。不同类型的“ 雾迷山旋回层” (a至f; 与图6-B所示相同)以及五级准层序组(①至⑦)在长周期三级层序中的有序叠加形式, 表明了米兰科维奇旋回地层记录的特征, 费希尔图解以DS10和DS20为例。A表示磨盘峪叠层石亚组合, 以胶结物相叠层石的发育为特征; B表示闪坡岭叠层石 亚组合的分布层位, 主要为泥晶相叠层石所组成）Fig.8 Diagram showing composite sequences of the Mesoproterozoic Wumishan Formation at Jixian section

如图3和图4所示, 在寒武系张夏组三级层序或四级亚层序的凝缩段单元(CS单元)中常常不发育米级旋回, 而且其中所发育的潮下型米级旋回常常向上变浅至鲕粒灰岩岩相单元(图 3-C)或泥晶灰岩岩相单元(图 2-B), 这些岩相单位所代表的实际古水深难以确定, 所以张夏组中的旋回难以用费希尔图解法来进行三级海平面变化幅度的模拟。雾迷山组中, 几乎每一个旋回层均向上变浅至海平面(图 7), 所以每一个旋回层的实际厚度与平均值的差值可以用来近似代表代表沉积物可容纳空间的变化, 用半定量的费希尔图解法来进一步模拟三级海平面变化旋回的变化幅度(如图8的三级层序DS10和DS20所示); 同时, 在雾迷山组中, 如图8的三级层序DS10和DS20所示, 常常4个旋回构成一组, 组成类似于层序地层学中的“ 准层序组” , 间接地表明了长偏心率旋回与短偏心率旋回的叠加关系, 也就是说, 每一个旋回层的形成时限可以假定为与短偏心率旋回周期相关的10万年, 根据这种假设前提, 还可以进一步估算三级层序的堆积作用时限。根据上述方法, 对雾迷山组露头出露完好的中上部地层(大致由626个旋回层组成图8中的DS8至DS26), 进行海平面升降幅度的半定量模拟以及三级层序的堆积作用时限的估算, 其结果(表 1)如下:(1)三级层序的厚度变化范围为79.1~196.0m, 平均为132.32m; (2)三级海平面的最大升降幅度为6~88m, 平均为44.63m; (3)三级海平面的总体上升幅度为 -40~73m, 平均为27.79m; (4)每一个三级层序所包含的旋回层个数为12~43个, 平均为33.05个; (5)由旋回层的形成时限可推断出三级层序的形成时限, 即变化范围为1.2~4.3Ma, 平均为3.31 Ma。

在传统地层学意义上为整合序列的雾迷山组之中, 代表地壳均衡沉降期的地层堆积作用特点、造成沉积物可容纳空间数米至数十米乃至百余米旋回性变化的驱动机制是三级海平面变化, 所得出的统计结果是叠加在一个地壳均衡沉降基础上的相对海平面变化旋回, 所识别出的三级层序的形成周期与奥尔特星系旋回周期(1~5Ma; 王鸿祯和史晓颖, 1998; 孟祥化和葛铭, 2004)具有良好的对应性。根据露头出露完好的中上部所发育的626个旋回, 再加上DS1至DS7中的近300个旋回层, 可以大致推断雾迷山组的地层堆积作用时限为100Ma左右, 但是从米兰科维奇信号所指示的时间是没有起始点的时间, 这个数据与王松山等(1995)所测的同位素数据:即1310± 20 Ma~1207± 10Ma大致吻合。但是, 随着蓟县剖面长期以来归到新元古界下马岭组的新年龄数据(大于1300Ma; 高林志等, 2007)的获得, 将雾迷山组归到延展系(王松山等, 1995; Gradstein et al., 2004; 章森桂等, 2009)的认识似乎应该改变, 雾迷山组可能应该归到盖层系上部。如表1所示的数据表明, 从地层记录中沉积旋回的叠加形式所反映的米兰科维奇信号可以近似地用来估计地层堆积作用的时限, 就像生物地层资料能提供地层上下关系的年代地层意义一样, 这种时间有可能成为误差较大的同位素测年数据的一种补充, 根据米兰科维奇信号对泥盆纪牙形石带分布时限的研究是这方面的典型实例(江大勇等, 1999; 郝维成等, 2000; 龚一鸣等, 2004); 其次, 沉积旋回的厚度变化可能近似地代表了三级海平面变化所产生的沉积物可容纳空间的变化, 这个信息不但可以用来帮助识别三级层序, 还可以运用费希尔图解法来大致估算三级海平面变化的升降幅度。这些方法学充分说明了旋回的研究是对简单定义的层序地层学中“ 准层序” 的良好补充, 而且代表了旋回地层学的一个主要研究内容, 为天文地层学的兴起(徐道一, 2005; 徐道一等, 2006)以及地质计时的“ 钟摆” 研究奠定了基础。

表1 天津蓟县剖面雾迷山组中上部三级层序的海平面变化幅度和形成时限统计 Table1 Statistic of sea level change amplitude and forming periods of the upper and middle parts of Wumishan Formation at Jixian section in Tianjin

将米级旋回所代表的沉积旋回解释为米兰科维奇旋回的产物的同时, 应该记住的是:由于轨道效应所造成的日照率只是影响到地球大气圈顶部的变化, 而且地球大气圈顶部所接受的日照率的变化还随着纬度而变化; 尽管对于大气— 海洋系统来说日照率的变化较为重要, 但是, 这些体系之间的相互作用非常复杂, 更为重要的是, 日照率变化与它对气候的影响之间还存在一个可能的时间滞后效应, 再加上还存在许多自旋回机制(Wilkinson et al., 1996, 1997a, 1997b, 1999)也可以形成像米级旋回所表现出的旋回性, 所以, 过程和产物之间的严格对等关系几乎不存在, 这就给在地层记录中提取准确的米兰科维奇信号带来了若干困难(Reading, 1996), 正如层序地层学将层序的形成解释为全球海平面变化时由于难以准确区分出区域构造运动影响而造成“ 噪声” 信号并由此带来解释的困难。从这一点上讲, 就容易理解对地层存在多少种划分方法就存在多少种地层学分支和地层单位的“ 多重地层划分” 的概念(Hedberg, 1959; Salvador, 1994; Gradstein et al., 2004), 因为每一种方法既存在自身的优势又存在若干不足。

4 结语

尽管国外学者将旋回地层学限定在研究与米兰柯维奇旋回相关的沉积旋回之上, 而且这种限定在理论上似乎欠完整, 但是, 今天已经进入了层序地层学与旋回地层学相互交融的时代。沉积旋回的研究, 尤其是在地层记录中提取米兰科维奇旋回信号, 不但是对“ 准层序” 的良好补充(就像基于地震地层学资料所建立的层序地层学概念体系解决了地层穿时性的本质一样), 沉积旋回的研究还可以提供一些有关地层记录的特殊信息如地层堆积作用的时限和对三级海平面变化幅度的半定量估算。虽然对这些信息的误差难以进行正确评价, 但毕竟探索出了一些可操作的方法。几代地质学家运用古生物资料提供的地层相对顺序、地球化学方法提供的近似时间数据编制的“ 地质年代表” 而赋予地质时间以具体含义, 尽管所取得的成果令人鼓舞, 但是, 即使在显生宙还存在需要完善的地方, 更不要说前寒武纪的盖层纪之类的术语所代表的复杂地质变化还需要进一步探索和解读。这也表明了地层学研究的艰难。由岩相序列代表的沉积旋回的研究不但是对层序地层学中“ 准层序” 的良好补充, 而且提供了一种获取地质时间信息的方法, 成为现今地层学研究的一个热点, 也为天文地层学的兴起提供了可操作的方法, 更为在地层框架内研究沉积相复杂时空变化的层序地层学提供了一些有用的方法和重要信息。因此, 从旋回到层序, 代表了从岩相序列到沉积相序列研究的相互补充和交融, 在促进地层学理论发展的同时, 也为提高油气勘探的成功率带来了许多重要的概念和可操作的方法。

作者声明没有竞争性利益冲突.

参考文献
[1] 陈留勤. 2008. 从准层序到米级旋回——层序地层学与旋回地层学相互交融的纽带[J]. 地层学杂志, 32(4): 447-454. [文内引用:2]
[2] 冯增昭. 1989. 碳酸盐岩岩相古地理学[M]. 北京: 石油工业出版社, 1-186. [文内引用:1]
[3] 冯增昭, 王英华, 张吉森, 等. 1990. 华北地台早古生代岩相古地理[M]. 北京: 地质出版社, 1-270. [文内引用:1]
[4] 冯增昭. 1994. 碳酸盐岩岩类学[M]. 见: 冯增昭, 王英华, 刘焕杰, 等. 中国沉积学. 北京: 石油工业出版社, 105-127. [文内引用:1]
[5] 高林志, 张传恒, 史晓颖, 等. 2007. 华北青白口系下马岭组凝灰岩锆石SHRIMP U-Pb定年[J]. 地质通报, 26(3): 249-255. [文内引用:1]
[6] 龚一鸣, 徐冉, 汤中道, 等. 2004. 广西上泥盆统轨道旋回地层与牙形石定年[J]. 中国科学(D辑), 41(1): 50-58. [文内引用:3]
[7] 郝维成, 白顺良, 江大勇. 2000. 法门阶上部米兰科维奇旋回在中国发育的一致性[J]. 科学通报, 45(15): 1654-1660. [文内引用:3]
[8] 黄学光, 贺玉贞, 王亚烈. 1996. 华北海泡石矿: 产状、成因和用途[M]. 北京: 地质出版社, 1-96. [文内引用:1]
[9] 江大勇, 郝维成, 白顺良. 1999. 广西泥盆系吉维特价上部地层中的化学旋回与米兰柯维奇偏心率的关系[J]. 科学通报, 44(9): 989-992. [文内引用:3]
[10] 陆元法, 李文汉. 1989. 旋回地层学[J]. 岩相古地理, 9(1): 31-40. [文内引用:1]
[11] 梅冥相. 1996. 淹没不整合型碳酸盐三级旋回层序——兼论碳酸盐台地的凝缩作用[J]. 岩相古地理, 16(6): 24-33. [文内引用:1]
[12] 梅冥相. 2010 a. 从正常海退与强迫型海退的辨别对层序界面的对比: 层序地层学进展之一[J]. 古地理学报, 12(5): 549-564. [文内引用:1]
[13] 梅冥相. 2010 b. 长周期层序形成机制的探索: 层序地层学进展之二[J]. 古地理学报, 12(6): [文内引用:1]
[14] 梅冥相, 梅仕龙. 1997. 华北中寒武世张夏组复合海平面变化旋回层序[J]. 沉积学报, 15(4): 5-10. [文内引用:2]
[15] 梅冥相, 高金汉. 2005. 岩石地层的相分析方法与原理[M]. 北京: 地质出版社, 1-285. [文内引用:5]
[16] 梅冥相, 高金汉, 孟庆芬, 等. 2008. 天津蓟县中元古界雾迷山组微指状叠层石及其对1250 Ma±叠层石衰减事件的响应[J]. 古地理学报, 10(5): 495-509. [文内引用:1]
[17] 孟祥化, 葛铭. 2004. 中朝板块层序·事件·演化[M]. 北京: 科学出版社, 1-483. [文内引用:1]
[18] 彭善池, Bobcock L E. 2005. 全球寒武系年代地层再划分的建议[J]. 地层学杂志, 29(1): 92-93, 96. [文内引用:2]
[19] 彭善池. 2006. 全球寒武系四统划分框架正式确立[J]. 地层学杂志, 30(2): 147-148. [文内引用:2]
[20] 彭善池, 2008. 华南寒武系年代地层系统的修订及相关问题[J]. 地层学杂志, 32(3): 239-245. [文内引用:2]
[21] 覃建雄, 张长俊, 王成善, 等. 1995. 全球旋回地层学[J]. 地质科技情报, 14(1): 17-22. [文内引用:1]
[22] 王鸿祯, 史晓颖. 1998. 沉积层序及海平面变化旋回的分类级别——旋回周期的成因讨论[J]. 现代地质, 12(1): 1-16. [文内引用:1]
[23] 王松山, 桑海清, 裘翼, 等. 1995. 蓟县雾迷山组和杨庄组形成年龄的研究[J]. 地质科学, 30(2): 166-172. [文内引用:1]
[24] 汪品先. 2006. 地质计时的天文“钟摆”[J]. 海洋地质与第四纪地质, 26(1): 1-7. [文内引用:1]
[25] 王英华, 张秀莲, 杨承运. 1994. 碳酸盐岩中的包壳粒[M]. 见: 冯增昭, 王英华, 刘焕杰, 等. 中国沉积学. 北京: 石油工业出版社, 128-152. [文内引用:1]
[26] 吴因业, 张天舒, 张志杰, 等. 2010. 沉积体系域类型、特征及石油地质学意义[J]. 古地理学报, 12(1): 69-81. [文内引用:1]
[27] 吴智勇, 姜衍文. 1996. 全球旋回地层学评述[J]. 石油与天然气地质, 17(1): 15-21. [文内引用:1]
[28] 徐道一. 2005. 天文地质年代表与旋回地层学研究进展[J]. 地层学杂志, 29(增): 635-640. [文内引用:3]
[29] 徐道一, 韩廷本, 李国辉, 等. 2006. 天文地层学的兴起[J]. 地层学杂志, 30(4): 323-326. [文内引用:3]
[30] 章森桂, 张允白, 严慧君. 2009. “国际地层表”(2008)简介[J]. 地层学杂志, 33(1): 1-10. [文内引用:3]
[31] 赵震, 1992. 核形石雏形——弥散粒: 以天津蓟县雾迷山组为例[J]. 沉积学报, 10(2): 19-27. [文内引用:1]
[32] Anderson E J, Goodwin P W. 1990. The significance of metre-scale allocycles in the quest for a fundamental stratigraphic unit[J]. J. Geol. Soc. London, 147: 507-518. [文内引用:3]
[33] Authur M A, Dean W E, Bottjer D, et al. 1984. Rhythmic bedding in Mesozoic-Cenozoic pelagic carbonate sequences: The primary and diagenetic origin of Milankevitch like cycles[C]. In: Berger, et al . Milankovitch and Climate, 1: 191-222. [文内引用:2]
[34] Berger A L. 1978. Long-term variation of daily insolation and Quaternary climatic changes[J]. Journal of Atmosphere Science, 35: 2362-2367. [文内引用:1]
[35] Berger A L, Loutre M F, Laskar J. 1992. Stability of the astronomical frequencies over the Earth’s history for paleoclimate studies[J]. Science, 255: 560-566. [文内引用:1]
[36] Catuneanu O, Martins-Neto M A, Eriksson P G. 2005. Precambrian sequence stratigraphy[J]. Sedimentary Geology, 176: 67-95. [文内引用:1]
[37] Catuneanu O. 2006. Principles of Sequence Stratigraphy[M]. Amsterdam: Elsevier, 1-375. [文内引用:2]
[38] Catuneanu O, Abreu V, Bhattacharya J P, et al. 2009. Towards the stand ardization of sequence stratigraphy[J]. Earth-Science Reviews, 92: 1-33. [文内引用:5]
[39] Fischer A G. 1964. The Lofer cyclothems of the Alpine Triassic[J]. Bulletin of Kansas Geological Survey, 169: 107-149. [文内引用:2]
[40] Fischer A G. 1980. Gibert bedding rhythms and geochronology[J]. GSA Special Papers, 183: 93-104. [文内引用:1]
[41] Fischer A G, Bottjer D J. 1991. Orbital forcing and sedimentary sequences[J]. Journal Sedimentary Petrology, 61(7): 1063-1069. [文内引用:4]
[42] Gómez J J, Fern-ndez-López S. 1994. Condensed processes in shallow platform[J]. Sedimentary Geology, 92: 147-159. [文内引用:1]
[43] Goldhammer R K, Dunn P A, Hardie L A. 1990. Depositional cycles, composite sea-level changes, cycle stacking patterns of the hierarchy of stratigraphic forcing: Examples from Alpine Triassic platform carbonates[J]. GSA Bulletin, 102(5): 535-562. [文内引用:3]
[44] Goodwin P W, Anderson E J. 1985. Punctuated aggradational cycles: A general hypothesis of episodic stratigraphic accumulation[J]. Journal of Geology, 93: 511-533. [文内引用:4]
[45] Gradstein F M, Ogg J G, Smith A G, et al. 2004. A new geological scale with special reference to Precambrian and Neogene[J]. Episodes, 27: 83-100. [文内引用:2]
[46] Hedberg H D. 1959. Towards a harmony in stratigraphic classification[J]. American Journal of Science, 257: 674-683. [文内引用:1]
[47] Hinnov L A. 2000. New perspectives on orbitally forced stratigraphy[J]. Annual Review of Earth and Planetary Sciences, 28: 419-475. [文内引用:1]
[48] Hinnov L A, Ogg J G. 2007. Cyclostratigraphy and the astronomical time scale[J]. Stratigraphy, 4: 239-251. [文内引用:1]
[49] Hunt D, Tucker M. 1992. Strand ed parasequences and the forced regressive wedge systems tract: Deposition during base level fall[J]. Sedimentary Geology, 81: 1-9. [文内引用:1]
[50] Klein G D, Willard D A. 1989. Origin of the Pennsylvanian coal-bearing cyclothems of North America[J]. Geology, 17: 152-155. [文内引用:1]
[51] Krapez B. 1993. Sequence stratigraphy of the Archaean supracrustal belts of the Pilbara Block, Western Australia[J]. Precambrian Research, 60: 1-45. [文内引用:2]
[52] Lasker J. 1999. The limits of earth orbital calculation for geological time-scale use[J]. Philosophical Transactions of Royal Society London, 1757: 1735-1759. [文内引用:1]
[53] Masetti D, Nero C, Bosellin A. 1991. Deep-water asymmetric cycles and progradation of carbonate platforms governed by high-frequence eustatic oscillations(Triassic of the dolomites, Italy)[J]. Geology, 19: 336-339. [文内引用:1]
[54] Mei Mingxiang, Xu Debin, Zhou Hongrui. 2000. Genetic types of meter-scale sequences and fabric natures of facies succession[J]. Journal of China University of Geosciences, 11(4): 375-382. [文内引用:12]
[55] Mei Mingxiang, Ma Yongsheng, Zhou Hongrui, et al. 2001 a. Fischer Plot of Wumishan cyclotherms, Precambrian records of third-order sea level changes[J]. Journal of China University of Geosciences, 12(1): 1-10. [文内引用:1]
[56] Mei Mingxiang, Ma Yongsheng, Guo Qingyin. 2001 b. Basic lithofacies-succession model for Wumishan cyclotherms: Their Markov chain analysis and regularly vertical stacking pattern in the third-order sequences[J]. Acta Geologica Sinica, 75(4): 421-431. [文内引用:1]
[57] Miall A D. 1984. Principles of Sedimentary Basin Analysis[M]. New York: Springer, 1-490. [文内引用:2]
[58] Miall A D. 1990. Principles of Sedimentary Basin Analysis(2nd edition)[M]. New York: Springer, 1-668. [文内引用:2]
[59] Milankovitch M. 1941. Karon der Erdstrahlung und seine Anwendung auf das Eiszcitproblem[J]. Akad R Serbe, 133: 1-633. [文内引用:2]
[60] Mitchum R, Vail P R, Thompson S. 1977. Seismic stratigraphy and global changes in sea level, part 2: The depositional sequence as the basic unit for stratigraphic analysis[C]. In: Payton C(ed). Seismic Stratigraphy : Applications to Hydrocarbon Exploration. AAPG Memoir, 26: 53-62. [文内引用:1]
[61] Mitchum R, Van Wagoner J. 1991. High frequency sequences and their stacking patterns: Sequence stratigraphic evidence for high frequency eustatic cycles[J]. Sedimentary Geology, 70: 131-160. [文内引用:3]
[62] Osleger D A. 1991. Subtidal carbonate cycles: Implications for allocyclic versus autocyclic controls[J]. Geology, 19: 917-920. [文内引用:2]
[63] Osleger D A, Read J F. 1991 a. Cyclostratigraphy of late Cambrian carbonate sequences[J]. SEPM Special Publication, 67: 801-828. [文内引用:1]
[64] Osleger D A, Read J F. 1991 b. Relation of eustasy and stacking patterns of meter-scale carbonate cycles, late Cambrian, U. S. A. [J]. Journal of Sedimentary Petrology, 61(7): 1225-1252. [文内引用:1]
[65] Posamentier H W, Allen G P. 1999. Siliciclastic Sequence Stratigraphy: Concepts and Applications[M]. Concepts in Sedimentology and Paleontology. SEPM Special Publication, 7: 1-210. [文内引用:1]
[66] Payton C. 1977. Seismic Stratigraphy: Applications to Hydrocarbon Exploration[M]. AAPG Memoir, 26: 1-516. [文内引用:1]
[67] Read J F. 1985. Carbonate platform facies models[J]. AAPG Bulletin, 69: 1-21. [文内引用:1]
[68] Reading H G. 1978. Sedimentary Environments and Facies[M]. Oxford: Blackwell Scientific Publication, 1-557. [文内引用:1]
[69] Reading H G. 1996. Sedimentary Environments: Processes, Facies and Stratigraphy[M]. Oxford: Blackwell Scientific Publication, 1-688. [文内引用:3]
[70] Salvador A. 1994. International Stratigraphic Guide(2nd edition)[M]. Boulder: International Union of Geological Sciences and Geological Society of America, 1-214. [文内引用:1]
[71] Sand er B. 1936. Beitrage zur Kenntnis der Anglagerungefuge[J]. Mineral Petrography, 48: 27-139. [文内引用:1]
[72] Schlager W. 1989. Drowning unconformities on carbonate platforms[C]. In: Crevello P D, Wilson J L, Sarg J F, et al. Controls on Carbonate Platform and Basin Development. SEPM Special Publication, 44: 15-25. [文内引用:1]
[73] Schlager W. 1998. Exposure, drowning and sequence boundaries on carbonate platforms[C]. In: Camoin G, Davies P. Reefs and Carbonate Platforms in the Pacific and Indian Oceans. International Association of Sedimentologists, Special Publication, 25: 3-21. [文内引用:1]
[74] Schlager W. 1999. Type 3 sequence boundaries[C]. In: Harris P, Saller A, Simo A. Carbonate Sequence Stratigraphy: Application to Reservoirs, Outcrops and Models. SEPM Special Publication, 63: 35-46. [文内引用:1]
[75] Schwarzacher W. 1975. Sedimentary Models and Quantitative Stratigraphy[M]. Amsterdam: Elsevier, 1-289. [文内引用:1]
[76] Schwarzacher W. 1993. Cyclostratigraphy and the Milankovitch Theory[M]. Amsterdam: Elsevier, 1-255. [文内引用:8]
[77] Sloss L. 1963. Sequences in the cratonic interior of North America[J]. GSA Bulletin, 74: 93-113. [文内引用:1]
[78] Spence G H, Tucker M E. 2007. A proposed integrated multi-signature model for peritidal cycles in carbonates[J]. Journal of Sedimentary Research, 77: 797-808. [文内引用:9]
[79] Strasser A, Hilgen F J, Heckel P H. 2006. Cyclostratigraphy—concepts, definitions, and applications[J]. Newsletters Stratigraphy, 42: 75-114. [文内引用:8]
[80] Van Wagoner J C, Posamentier H W, Mitchum R M, et al. 1988. An overview of sequence stratigraphy and key definitions[C]. In: Wilgus C K, Hastings B S, Kendall C G St C, et al[eds]. Sea Level Changes-An Integrated Approach. SEPM Special Publication, 42: 39-45. [文内引用:3]
[81] Van Wagoner J C, Mitchum R M, Campion K M, et al. 1990. Siliciclastic sequence stratigraphy in well logs, cores and outcrops[J]. AAPG Methods in Exploration, 7: 1-55. [文内引用:3]
[82] Vail P R, Mitchum Jr R M, Thompson S. 1977. Seismic stratigraphy and global changes of sea level, part 3: Relative changes of sea level from coastal onlap[C]. In: Payton C E(ed). Seismic Stratigraphy—Applications to Hydrocarbon Exploration. AAPG Memoir, 26: 63-81. [文内引用:1]
[83] Walker R G. 1984. General introduction: Facies, facies sequence and facies model[C]. In: Walker R G. Facies Models. Geological Association of Canada, Geoscience Canada Reprint Series, 1: 1-9. [文内引用:1]
[84] Wilgus C K, Hastings B S, Kendall C G St C, et al. 1988. Sea Level Changes—An Integrated Approach[M]. SEPM Special Publication, 42: 1-499. [文内引用:1]
[85] Wilkinson B H, Diedrich N W, Drummond C N. 1996. Facies succession in peritidal carbonate sequences[J]. Journal of Sedimentary Research, 66: 1065-1078. [文内引用:3]
[86] Wilkinson B H, Drummond C N, Rothman E D, et al. 1997 a. A stratal order in peritidal carbonate sequences[J]. Journal of Sedimentary Research, 67: 1068-1082. [文内引用:1]
[87] Wilkinson B H, Drummond C N, Diedrich N W, et al. 1997 b. Biological mediation of stochastic peritidal carbonate accumulation[J]. Geology, 25: 847-850. [文内引用:1]
[88] Wilkinson B H, Drummond C N, Diedrich N W, et al. 1999. Poisson process of carbonate accumulation on Paleozoic and Holocene platform[J]. Journal of Sedimentary Research, 69: 338-350. [文内引用:1]