作者简介:伊海生,男,1959年生,1989年毕业于成都理工大学,获理学博士学位,现为成都理工大学沉积地质研究院教授,博士生导师,长期从事沉积地质学的研究工作。电话:028-84079491(办);E-mail:yhs@cdut.edu.cn。
在碳酸盐岩台地沉积层序的研究中,通过旋回计数和厚度测量,采用费希尔图解法解析高频米级旋回或副层序的叠置形式和空间结构,进而标定三级沉积层序的界面,是目前普遍采用的一个方法。但是,这一方法目前主要用于露头层序地层学研究,而在地下油气勘探区受到极大的限制。文中提出了一种新的计算方法,它可以根据测井资料求取任一地层段沉积旋回的个数和厚度。根据数值模拟,详细讨论了海平面变化周期和幅度与沉降速率、沉积速率的相关关系,提出高频沉积旋回的分布模式和叠加样式可以指示低频海平面变化的轨迹,这为划分三级沉积层序、标定层序界面提供了理论依据。最后,以川西北地区中三叠统雷口坡组为例,说明了应用自然伽马测井资料进行数据处理的流程和步骤,以及根据旋回厚度累积偏差曲线标定层序界面的位置、识别旋回谱系标志。
The Fischer Plot is a graphic method about analyzing numbers and thicknesses of meter scale cycle units or parasequences of carbonate platform successions.The method is used to analyze the stacking patterns and hierarchical architectures of high frequency cycles and then to define depositional sequence surfaces.This method has widespread application in field stratigraphic sections,but it meets obstacles and limitations in subsurface petroleum exploration districts.A new calculation method is proposed in this paper and the cycle numbers and thicknesses can be detected by means of well log data processing in any stratigraphic intervals.The interplays among amplitudes and periodicities of eustatic sea levels,subsidence rates,and sedimentation rates were discussed in detail according to numerical simulation results.It is suggested that ordered stacking patterns of high frequency cycles indicate low frequency sea level fluctuation pathways.This provides us theoretical basis to distinguish the third order depositional sequences and surface location with well depth.The Middle Triassic Leikoupo Formation in the northwestern Sichuan Basin is taken as a case study,processing methods and procedures were demonstrated using natural gamma ray logging data.Discriminant markers for depositional sequence surfaces and multiple cyclic hierarchies were presented by graphing cumulative departure curves from mean cycle thickness as a function of cycle number or well depth.
在碳酸盐岩沉积层序的研究中, 根据岩相类型和水深标志识别沉积旋回, 通过旋回计数和厚度测量, 研究这些高频米级旋回的叠置形式和空间结构, 进而标定三级沉积层序的界面, 是目前在海相碳酸盐岩沉积区普遍采用的一个方法(马永生, 1994; 蔡忠贤等, 1997; 章雨旭等, 1997; 陈建强等, 1998; 柳永清等, 1999; 齐永安和胡斌, 2000; 梅冥相等, 2001; 周洪瑞等, 2006)。Fischer(1964)和Goldhammer等(1987)早期对欧洲阿尔卑斯地区三叠系Lofer旋回和Latemar旋回的研究就是这方面的经典实例, 嗣后, Read和Goldhammer(1988)、Koerschhner和Read(1989)、Osleger和Read(1991)根据潮坪相碳酸盐岩旋回的个数和厚度变化, 建立了北美阿帕拉契亚地区寒武纪、奥陶纪海平面变化曲线。在中国华北、塔里木和鄂尔多斯等地, 一些学者对以潮坪相鲕粒滩型和以白云岩为主的米级旋回垂向叠加形式以及旋回组合的谱系和配置关系进行了深入的研究, 证实这些沉积旋回受地球轨道参数周期性变化的控制, 旋回组合谱系对应于米兰科维奇天文周期驱动的高频海平面变化。根据米级旋回层序在垂向上的有序叠加型式, 即地层剖面中旋回厚度增加或减小所呈现的加积、退积和进积型的变化趋势, 可以进一步识别和划分三级沉积层序和体系域。但是, 该方法目前主要用于露头层序地层学研究, 而对一般油气勘探区无岩心或岩心采收率低的探井, 这一方法的应用受到极大的限制; 而且如何客观正确地划分沉积旋回, 将直接影响旋回厚度测量和旋回计数的结果。例如, 以海侵面(风暴滞留层)和暴露面(古喀斯特)与以水深为标志划分的沉积旋回数目可能有所不同, 而且人工测量的旋回厚度, 如果对旋回界面识别缺乏统一的标准, 可能还会产生米级到数米级的误差。
地球物理测井曲线具有等间距采样的特点, 而且数据序列连续、纵向分辨率高, 可以作为检测米级高频旋回、划分三级沉积层序的主要资料(陈茂山, 1999; 郑兴平等, 2004)。采用对岩性变化响应特别敏感的自然伽马测井数据, 作者提出通过一种新的计算方法, 即一阶差分法, 计算任一地层段沉积旋回的个数和厚度。这是识别高频和低频海平面变化信号的最基本的单元。通过编绘旋回厚度偏差随深度的变化曲线, 不仅可以判别不同级别的旋回层序, 还可以准确地标定三级层序界面在地层剖面上的位置。文中首先通过数值模拟技术, 解释了高、低频海平面变化与沉积速率和沉降速率之间的关系, 论证了应用高频沉积旋回空间叠置型式解析低频海平面变化过程的原理, 并以四川盆地西部三叠系雷口坡组为例, 说明了应用测井资料求取沉积旋回的数据计算过程和处理流程。
全球海平面变化是层序地层学的重要理论基础和核心内容。高频海平面变化是指四、五和六级与米兰科维奇天文周期有关的海平面振荡变化(Haq et al., 1987; Vail et al., 1991)。研究表明, 短时序(20~400 ka)的米兰科维奇周期变化引起了陆地冰盖的消融和扩张, 控制了高频海平面升降旋回, 米兰科维奇旋回周期(M)反映了地球轨道参数的变化, 它包括地球轨道的长和短偏心率周期(400 ka和100 ka)、地轴斜率周期(54 ka和41 ka)和岁差周期(23 ka和19 ka)。据资料, 在冰室期由米兰科维奇旋回驱动的高频海平面升降幅度波动最高可达150m, 温室期要低, 一般在25m左右(Berger et al., 1990; Pomar, 1991; Abreu and Anderson, 1998; Pillans et al., 1998; Miller et al., 2003), 并且在地质历史时期的地层记录中保存了普遍的印迹。目前, 在古代浅海碳酸盐岩地层中不但已经识别出了四级和五级(400 ka和100 ka)的长短偏心率周期, 而且在深海泥灰岩— 泥岩韵律沉积中也发现了六级(20 ka)的岁差周期(Einsele and Seilacher, 1991; Schwarzacher, 1993; Weedon, 2003)。
层序地层学关注的是冰川或构造驱动的长周期三级海平面变化, 其周期介于0.5~5 Ma(王鸿祯和史晓颖, 1998)。一般认为三级海平面变化具有幕式旋回的特点(episodic cycles, Haq et al., 1987; Vail et al., 1991), 但也有人提出它反映了米兰科维奇长周期变化, 具有周期性波动的特点(periodic oscillation, Schwarzacher, 1993)。
这些低频长周期和高频短周期海平面波动都有其特征的振幅和频率, 它们相互叠加产生全球海平面波动。全球海平面变化和构造沉降速率、沉积供给速率三者之间相互作用并在时间和空间上形成一系列复杂的地层叠置样式。
为了直观、定量地反映全球海平面振荡变化周期、振幅变化与区域沉降速率以及沉积速率之间的关系, 下面采用数值模拟图解的方法予以说明。
按照Weedon(2003)提出的旋回地层学中时间序列分析理论, 任意一个海平面波动过程可以采用正弦波数学模型来描述, 每一个正弦波包括频率、周期和相位3个要素, 而全球海平面的变化轨迹则可以采用这些频率和振幅不同的正弦函数波的复合叠加曲线表示。图1中长周期海平面变化周期设定为1 Ma, 振荡幅度设定为± 20m, 高频海平面变化周期分别设定为100 ka和20 ka, 对应米兰科维奇旋回的偏心率和岁差周期, 振幅设定为± 5m, 则全球海平面或复合海平面随时间升降的变化曲线可通过下式计算:
复合海平面变化曲线=20 m× sin(1/1000 ka)+5 m× sin(1/100 ka)+5 m× sin(1/20 ka)
图1中横坐标表示时间, 以ka为单位, 纵坐标为海平面升降幅度, 正值指示海平面上升, 负值指示海平面下降。图中蓝色曲线表示频率 为1/1000、 1/100 和1/20的3 个正弦波叠加产生的复合海平面变化曲线, 红色曲线表示长周期三级海平面变化轨迹, 显示在时间长度为2 Ma的区间内, 复合叠加海平面变化化曲线上存在2个长周期、频率 为1/1000的 低频正弦波动, 升降幅度为 ± 30 m。 按照Haq等(1987)和Vail等(1991)的层序地层学理论, 复合海平面变化具有全球一致性, 是进行地层区域对比的基础; 如果海平面波动的周期不变, 则海平面振幅愈大, 海平面变化速率愈高; 而低频海平面变化曲线上的拐点, 即海平面变化速率最大值或最小值的转换点, 对应三级层序界面或层序内部单元分界线的位置。
构造沉降(T)是地壳热沉降和构造载荷引起的盆地基底下沉量两者之和。当构造沉降速率增加时, 盆地中同一地点水深增加, 反之则水深减小。据资料, 被动大陆边缘盆地沉降速率低, 一般为0.01~0.025 m/ka, 而以热沉降为主的克拉通盆地到以挠曲沉降为主的前陆盆地, 沉降速率变化为0.01~0.4 m/ka(Angevine et al., 1990)。
全球海平面变化与构造沉降之和决定了相对海平面升降幅度, 进而控制了沉积物可容纳空间的大小。如果全球海平面变化速率保持不变, 区域构造沉降速率愈大, 则沉积盆地的可容纳空间增加越快, 两者之间关系如图2所示。一般来说, 在同一个沉积盆地中, 其盆地边缘的沉降速率小于盆地中心位置的沉降速率, 而且不同沉积时段构造沉降速率还可能有所差别, 因此将会产生一系列复杂的相对海平面变化模式。在三级海平面变化的时间尺度上, 由于海平面变化幅度远大于构造沉降量, 一般假定构造沉降速率为一个常数, 即沉降速率随时间呈线性变化(Read et al., 1986)。图2中分别设定沉降速率为0.025 m/ka和0.055m/ka, 全球海平面变化参数与图1相同, 从图中全球海平面变化与沉降速率叠加产生的2条相对海平面变化曲线可以看出, 随着沉降速率增加, 相对海平面升降幅度和沉积物可容纳空间明显增加。
沉积速率是指海洋或湖泊沉积物在一定时间内在单位面积上堆积的地层厚度。根据McNeill(2005)对第四纪沉积速率的研究, 碳酸盐岩台地的平均沉积速率一般为0.01~0.05 m/ka, 但变幅极大, 最大可达2 m/ka。
海平面变化速率、沉降速率和沉积速率3者之间存在以下函数关系:
相对海平面变化速率(RS)=全球海平面变化速率(ES)+沉降速率(T)
可容纳空间变化速率(A)=相对海平面变化速率(RS)
全球海平面变化速率(ES)+沉降速率(T)=水深变化速率(W)+沉积速率(S)
相对海平面升降幅度=沉积速率× 时间+水深变化速率× 时间
对于任一时间点的水深和沉积高度(地层厚度), 可通过下式计算:
水深=可容纳空间变化速率(A)× 时间— 沉积速率× 时间
沉积高度=可容纳空间变化速率(A)× 时间— 水深变化速率× 时间
当可容纳空间变化速率大于沉积速率时, 即A> S, 这时沉积厚度或沉积高度仅与沉积速率有关; 反之, 如果可容纳空间变化速率小于沉积速率时, 即A< S, 这时沉积厚度受海平面高度控制, 两者关系如图3中时间点T1、T2、T3和T4所示。
如果全球海平面变化速率和构造沉降速率恒定, 当沉积速率为0时, 可容纳空间最大, 海平面升降高度等于水深; 当沉积速率大于可容纳空间变化速率时, 所有的可容纳空间都为沉积物充填, 这时沉积高度等于海平面升降幅度; 而在沉积速率小于可容纳空间变化速率的情况下, 只有部分可容纳空间为沉积物充填, 剩余空间为水体占据, 如图3所示。
层序地层等时对比的理论核心是海平面变化具有全球同步的特点, 而低频长周期海平面变化旋回又调控着高频海平面变化的形式和升降幅度, 因此以地层记录中高频沉积旋回厚度作为一个参数, 论证高频旋回厚度与三级海平面旋回过程的关系。
要求解沉积旋回厚度与全球海平面波动周期及幅度之间的关系, 关键是要将ka级时间坐标单位(时间域数据系列)转换为m级深度域数据系列。如果引入一个变量, 称为旋回厚度偏差,
 | 图4 旋回沉积厚度与沉积速率之间的关系Fig.4 Relationship between depositional thickness of a cycle and sedimentation rate |
即每个旋回厚度与其平均厚度值之差, 标记为± C, 其值可正可负, 就可以将时间域转换为深度域, 进而评估高频旋回叠置样式与三级海平面变化之间的关系。兹以图4和图5说明计算过程和结果。首先, 假设沉降速率为常数, 取0.055 m/ka作为计算值, 复合海平面变化的周期和振幅设定与图1和图2相同。为了简化计算过程, 计算时间长度取2000 ka, 时间坐标间距设定为1 ka, 则根据共计2000个数据点计算的可容纳空间变化曲线如图4-A所示。以任一周期作为步长, 对时间单位进行等间距采样, 则可求一个高频旋回的个数。图4-B中设定采样间距为10 ka, 则在时间长度为2000 ka的区间内, 计有200个周期为10 ka的数据点。设定不同的沉积速率变量, 根据沉积高度与沉积速率和可容纳空间变化速率之间的关系, 可求得每一个数据点的沉积厚度。图4-B表示沉积速率大于、小于和等于沉降速率时沉积厚度随时间变化的曲线。
为了考察沉积物堆积速率与可容纳空间变化速率之间的关系, 按旋回个数或旋回厚度分别计算了累积旋回厚度偏差, 其值与旋回数或深度的关系如图5所示。为了对比研究累积旋回厚度偏差曲线与长周期沉积层序界面的对应关系, 图5中同时标绘了全球海平面变化曲线。
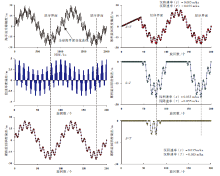 | 图5 累积旋回厚度偏差与全球海平面变化关系的图解Fig.5 Diagram showing relationship between cumulative cycle thickness departures and eustatic sea level changes |
从图5模拟计算结果可以发现, 如果全球海平面升降幅度和区域构造沉降速率一定, 随着沉积速率的变化, 旋回厚度偏差及其随时间的变化可能出现如下几种情况:
1)当沉积速率极高, 或沉积速率远大于沉降速率时, 即S> > T时, 由于沉积堆积厚度一般小于海平面高度, 这时高频沉积旋回的累积偏差曲线与低频海平面波动曲线一致, 累积旋回偏差曲线的波动幅度等于低频海平面波动幅度。这种情况常出现在浅水碳酸盐岩台地沉积区, 在阿尔卑斯三叠纪潮坪环境发育的Latermar旋回和Lofer旋回都是这一方面的实例(Anderson et al., 1990, Goldhammer et al., 1990, Osleger et al., 1990)。相反地, 如果沉积速率极低, 或者沉降速率等于或大于沉积速率, 即T≥ S时, 如在海盆深水区, 出现低速凝缩段沉积, 则沉积节律缺失。
2)在正常的海洋环境中, 沉积物堆积速率一般大于盆地沉降速率。分别取中等沉积速率0.055 m/ka和0.085 m/ka进行模拟计算, 结果如图5所示:旋回厚度累积偏差曲线与海平面变化曲线相比较不但发生了变化, 而且旋回厚度累积偏差曲线升降的幅度也明显小于海平面变化幅度, 但值得注意的是两条曲线升降转换节点的位置相同。这个结果提供了一个重要启示, 即高频旋回厚度累积偏差曲线并不一定能直接标定低频海平面变化幅度, 但在地层序列中旋回厚度累积曲线升降拐点指示沉积层序界面的位置, 这就为应用测井曲线划分沉积旋回, 进而判别三级沉积层序界面提供了理论依据。
四川盆地毗邻龙门山的西北部地区, 三叠系碳酸盐岩台地相广泛发育, 地层序列齐全, 分界标志明显, 是观察了解扬子地区三叠纪沉积层序和海平面变化级次的一个窗口。目前, 石油勘探部门已经在川西地区雷口坡组碳酸盐岩地层中探明了油气藏, 积累了一批测井资料, 这为研究碳酸盐岩高频旋回层序提供了一个最好的场所。兹以川西江油青林1井为例, 说明应用自然伽马测井数据计算沉积旋回厚度、划分沉积层序、标定层序界面的方法。
四川盆地西北部中三叠统雷口坡组(T2l)厚200~1000m, 主要由一套潮坪— 潟湖相白云岩组成, 中下部夹膏盐岩, 顶部见少量的灰岩; 雷口坡组与下伏嘉陵江组(T1j)白云岩为整合接触, 两组之间以1层层厚数米的“ 绿豆岩” 分界, 顶部与上覆的须家河组(T3x)碎屑岩之间以不整合面分隔, 以岩性突变面作为识别标志。
根据对江油马脚坝地区雷口坡组地表剖面和钻井岩心的观察, 雷口坡组可分3段, 其中雷三段进一步细分为上亚段和下亚段。雷一段由薄层状深灰色粉细晶白云岩、黄灰色膏质白云岩组成, 夹石膏层; 雷二段岩性为深灰色粉细晶白云岩、膏质白云岩和灰白色石膏层, 局部层位见鲕粒白云岩; 雷三段下亚段以发育褐灰色针孔状白云岩、藻粒白云岩、鲕粒白云岩、云质灰岩为特征, 底部以深灰色灰岩层与雷二段分界。雷三段上亚段以深灰色、褐灰色粉细晶白云岩为主, 局部层位见砂屑和藻屑白云岩。
测井曲线是一系列深度域振动信号序列的组合, 它是时间域周期性变化的叠加响应。测井曲线具有等间距采样的特点, 而且数据序列连续、纵向分辨率高, 因此可以满足数学含义上时间序列分析的基本要求(李庆谋, 1996; 陈茂山, 1999)。在常规测井曲线中, 自然伽马曲线能最敏感地反映泥质含量变化, 有效记录地层序列中沉积旋回的特点, 因而在高频旋回地层研究中得到了广泛应用(张占松, 2000; 李霞等, 2006; 吴怀春等, 2008)。
青林1井雷口坡组深度位于3562~4056m, 地层厚度494 m。为了全面了解雷口坡组米级沉积旋回的叠置样式, 选择同一深度的自然伽马数据进行研究, 共计采集数据点3952个, 测量间距0.125m, 自然伽马值变化范围在30~65 API。 自然伽马测井是测量地层中放射性元素衰变过程中放射出的伽马射线的强度, 其值大小取决于岩石中所含放射性核素(铀、钍、钾)的种类和数量。一般伽马高值对应泥岩, 低值对应石灰岩或白云岩。地层剖面中泥质含量从低到高的变化, 相应地反映了从石灰岩或白云岩到泥灰岩或泥岩的沉积旋回。
根据青林1井雷口坡组伽马值, 通过Excel提供的函数程序, 计算沉积旋回厚度并进行旋回个数计数的步骤如下:
1)首先采用线性内插法对原始数据进行校正, 求取等间距数据序列。
2)为了消除系统误差和测井曲线的长趋势偏移, 采用最小二乘法对原始曲线进行拟合, 取其与原数据序列之差作为新数据序列。
3)采用移动平均法过滤背景噪音, 突出沉积旋回的周期波动。移动平均的周期视旋回的大小而定, 实际计算过程中采用5点移动平均值消除高频噪音。
4)由于预处理过程中采用参数的差异, 可能造成计算结果的误差, 因此必须使数据中心化或归一化。实际计算过程采用一阶差分法处理, 保证最终计算结果具有一致性。
5)最后采用逻辑判别函数, 提取归一化伽马测井数据序列正负偏差数据, 计算出沉积旋回厚度。
图5是计算结果, 根据伽马测井数据, 求出青林1井雷口坡组计有238个高频沉积旋回, 旋回厚度变化为0.5~5.5m, 旋回平均厚度为2.1 m。
应该强调, 如果测井数据操作处理方法不同, 可能造成伽马数据的计算结果有一定的差别, 但在以上处理流程中, 伽马数据仅是一个用来求取旋回厚度的过渡参数, 旋回厚度的计算结果仅涉及伽马数据的相对变化幅度而与其绝对值大小无关。
根据青林1井雷口坡组旋回个数和厚度, 取纵坐标为旋回数, 或者以井深为纵坐标, 横坐标为累积旋回厚度偏差, 以米为单位, 可编绘2条旋回厚度偏差曲线, 结果如图6所示。分析旋回组合及其叠加样式在地层剖面中的变化, 可以识别层序界面和层序结构。
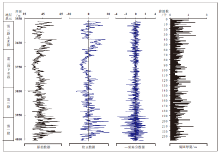 | 图6 川西北地区青林1井应用自然伽马测井数据计算旋回数及厚度的处理流程Fig.6 Procedure of cycle number counting and thickness calculation from natural gamma ray logging data of Well Qinglin 1 in northwestern Sichuan area |
从图7中可以看出, 高频旋回厚度的累积偏差曲线表现为多级次组合谱系。按照旋回厚度累积偏差曲线的波动特征, 雷口坡组中至少可以识别出2个低频变化周期, 其曲线形态表现出低缓波状起伏且近于对称的特点, 两者分界在井深为3885m的位置。根据生物地层资料和火山成因绿豆岩测年数据(胡世玲等, 1996), 初步认为这2个低频变化周期可能对应于三级海平面变化, 曲线转换点在井深3885m处对应于海平面下降最低点, 即三级层序界面的位置, 最高点对应最大海泛期即凝缩段层位。进一步研究还可以发现, 在三级低频海平面变化曲线上, 叠加有一系列尖突的锯齿状波峰, 这在海平面上升曲线上表现得最为明显。如雷口坡组上部三级层序中可以观察到8个高频旋回组合, 下部三级层序中可以观察到6个高频旋回组合, 每个旋回组合分别由13个到16个高频旋回组合而成。这些旋回组合是构成海侵— 海退沉积旋回的重要单元, 相当于一般三级层序的准层序组或高级别的四级亚旋回(王鸿祯和史晓颖, 1998)。
以伽马数据为基准刻度的沉积旋回, 主要反映了碳酸盐岩地层剖面中泥质含量的周期性变化, 它与以岩性为标志所鉴别的沉积旋回有所差别。例如, 在地表露头剖面和钻井岩心中雷口坡组至少可识别出蒸发岩— 白云岩、藻屑白云岩— 膏质白云岩、鲕粒白云岩— 粉晶白云岩几种类型。但根据测井曲线求得的沉积旋回, 可能包含2个或2个以上的岩相类型, 也可能在同一个岩相中划分出多个沉积旋回。
 | 图7 川西北地区雷口坡组层序地层划分及界面Fig.7 Division of sequence stratigraphy and sequence surfaces of the Leikoupo Formation in northwestern Sichuan area |
一般而言, 碳酸盐岩中的泥质组分相对比较稳定, 很少受到成岩期的溶解或交代作用而损失。同时, 在浅海碳酸盐沉积环境中, 泥质含量主要受进入海洋的河流径流量以及沉积物输入量大小的控制, 而河流的泥沙通量又与气候的冷暖干湿变化周期有关。因此, 以伽马值作为泥质含量变化的指标, 不但可以反映米兰科维奇旋回驱动的陆地气候变化, 还可能同步放大高频海平面波动的信号(Ten Veen and Postma, 1996; 刘泽纯等, 2000)。
应用沉积旋回厚度变化重建过去的海平面变化的一个前提条件是每一个沉积旋回单元形成的持续时间必须相同, 即按一定标志划分的沉积旋回是等时间隔的地层单元。这样才能应用地球轨道旋回周期时间间隔固定的特性, 建立高低频复合海平面变化的地层响应和谱系, 进而识别沉积层序的等级和界面。但是, 在地表露头和钻井岩心中, 通过观察测量以岩性特征或水深标志划分的沉积旋回, 很难保证每个旋回都是等时间隔的地层单元。构成沉积旋回的岩性类型愈多, 由于不同岩性的沉积速率不可能相同, 这时造成的误差可能更大(马永生, 1994; 章雨旭等, 1997; 陈建强等, 1998; 齐永安和胡斌, 2000; 柳永清等, 2001; 梅冥相等, 2001; 周洪瑞等, 2006)。而应用伽马物理测井数据反映的泥质含量的变化来识别沉积旋回, 因为旋回的划分采用同一标准, 因此可以最大限度地保证旋回之间持续时间的一致性, 减小重建的海平面变化曲线的误差。
采用旋回个数或钻井深度作为纵坐标, 用旋回平均厚度累积偏差值作为横坐标, 通过图解法编绘的曲线展现的是一个多级次的旋回组合谱系。对旋回层序进行分级是首先需要面对的问题, 这是因为三级沉积层序的边界是进行沉积盆地一级地层对比的等时界面(王鸿祯和史晓颖, 1998)。对旋回谱系进行分级, 最关键的问题是对测井数据所能分辨的最小沉积旋回单元的时间长度进行标定。目前普遍采用2个方法:其一是根据生物地层资料、古地磁极性带以及同位素测年数据确定地层组段顶底界时限, 根据沉积旋回以及旋回组合形成的时间范围, 分析它们与高低频海平面变化周期的对应关系, 划分层序级次。其二, 由于高频海平面振荡受米兰科维奇天文周期控制, 而米兰科维奇天文周期之间具有固定的比例关系, 因此在三级层序中高频沉积旋回表现出有序的叠加型式。例如, 长偏心率周期(400 ka)和短偏心率周期(100 ka)的比值为1:4; 短偏心率(100 ka)与岁差周期(20 ka)的比值为1:5, 它们在地层剖面上表现为5个沉积旋回组合成一组, 相当于三级层序的准层序组, 这是因为偏心率周期控制岁差周期的振幅变化, 这时在旋回厚度累积偏差曲线上形成一个尖锐的波峰; 4个短偏心率旋回组合可归并为一个更高一级的长偏心率组合, 对应三级层序的准层序组, 这时在旋回厚度累积偏差曲线上形成一个平缓的波峰。根据这个比例关系, 如果根据年代地层资料或沉积速率, 能够初步确定研究层段的沉积旋回的平均时限属于岁差周期还是偏心率周期, 就可以根据旋回厚度累积偏差曲线上波峰和波谷的高低变化分辨旋回的级次。
1)通过数值模拟和图解方法, 论证了碳酸盐岩台地的旋回性地层沉积特征与高频和低频海平面变化之间的成因联系。高频旋回地层单元的分布模式受全球海平面变化、盆地沉降速率和沉积速率3个因素的联合控制, 高频沉积旋回单元的分布模式和叠加样式可以指示低频海平面变化的轨迹, 这为划分三级沉积层序、标定层序界面提供了理论依据。
2)测井曲线具有等间距采样的特点, 而且数据序列连续、纵向分辨率高, 特别是自然伽马曲线能敏感地反映碳酸盐地层中泥质含量的变化, 可以作为识别高频沉积旋回最有效的手段。一种新的计算方法, 即一阶差分法, 可以根据测井资料计算任一地层段沉积旋回的个数和厚度。
3)为了研究高频沉积旋回和旋回组合在地层剖面上的分布模式及其方向性变化, 引入了旋回厚度偏差这一参数, 通过编制二维图解来研究沉积旋回的叠置样式和配置关系, 进而根据曲线上多谱系旋回级次的突变点准确标定层序界面的位置。
4)以四川盆地西北部中三叠统雷口坡组为例, 详细说明了应用自然伽马测井资料进行旋回计数、编制旋回厚度偏差曲线的数据校准步骤和处理流程, 讨论了过去以岩相类型划分的沉积旋回与测井曲线识别的沉积旋回之间的异同点。同时, 应该强调指出, 快速构造沉降或长期暴露侵蚀, 都可能造成高频旋回间断缺失或凝缩归并而失去韵律性, 预计该方法更适用于海平面变化速率与碳酸盐生产力处于平衡状态的碳酸盐岩台地沉积区。
作者声明没有竞争性利益冲突.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|
| [28] |
|
| [29] |
|
| [30] |
|
| [31] |
|
| [32] |
|
| [33] |
|
| [34] |
|
| [35] |
|
| [36] |
|
| [37] |
|
| [38] |
|
| [39] |
|
| [40] |
|
| [41] |
|
| [42] |
|
| [43] |
|
| [44] |
|




