地震流体识别方法在四川盆地页岩气“甜点”预测中的应用<sup>*</sup>

黄捍东, 纪永祯, 张骋, 刘承汉. (2013)地震流体识别方法在四川盆地页岩气“甜点”预测中的应用^* [J]. 古地理学报, 15(5): 672-678
Huang Handong, Ji Yongzhen, Zhang Cheng, Liu Chenghan. (2013)Application of seismic liquid identification method in prediction of shale gas “sweet spots” in Sichuan Basin[J]. Journal Of Palaeogeography, 15(5): 672-678. DOI:10.7605/gdlxb.2013.05.055 复制到剪切板

Permissions

地震流体识别方法在四川盆地页岩气“甜点”预测中的应用^*

黄捍东^1,², 纪永祯², 张骋³, 刘承汉⁴

1 中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249

2 中国石油大学(北京)提高采收率研究院,北京 102249

3 中国石油大学(华东)地球科学与技术学院,山东青岛 266580

4 长江大学地球物理与石油资源学院,湖北武汉 430100

第一作者简介: 黄捍东,1964年生,2000年毕业于成都理工大学,获博士学位。现为中国石油大学(北京)教授、博士生导师,主要研究方向是复杂油气藏储集层预测与流体识别。

收稿日期:2013-05-09

基金:*国家重大专项“南堡凹陷油气富集规律与增储领域”(编号:2011ZX05006-006)、国家973专项“深部有效碎屑岩储集层成因机制与发育模式”(编号:2011CB201104)和“低渗透油田弹性驱替界限与开发后期井网优化调整技术研究”(编号:2011ZX05009)联合资助

摘要

中国页岩气资源丰富,但勘探水平相对较低。在钻井、测井资料匮乏的条件下,高精度地震流体检测方法的研究至关重要。从地震弹性波方程入手导出了流体活动因子表达式,该因子与储集层密度、黏度和渗透性成正比。将流体活动因子分析与高精度时频分析结合,形成用于页岩气“甜点”预测的实用方法,即首先基于高精度时频分析,分析流体的时频特性,计算出流体活动因子,进而与测井资料结合量化页岩气“甜点”区流体活动因子的范围,从而预测页岩气“甜点”分布区。该方法在四川盆地的应用表明,其预测结果与钻井、测试结果吻合,取得了良好的勘探效果,对页岩气勘探具有重要的指导作用。

关键词: 页岩气; 流体活动因子; 地球物理方法; 四川盆地

中图分类号:P631 文献标志码:A 文章编号:1671-1505(2013)05-0672-07

Application of seismic liquid identification method in prediction of shale gas “sweet spots” in Sichuan Basin

Huang Handong^1,², Ji Yongzhen², Zhang Cheng³, Liu Chenghan⁴

1 State Key Laboratory for Petroleum Resources and Prospecting,China University of Petroleum(Beijing),Beijing 102249

2 Institute of Enhanced Oil Recovery,China University of Petroleum(Beijing),Beijing 102249

3 School of Geosciences,China University of Petroleum(East China),Qingdao 266580,Shandong

4 School of Geophysics and Resources of Yangtze University,Wuhan 430100,Hubei;

About the first author:Huang Handong,born in 1964,graduated from Chengdu University of Technology with a doctoral degree in 2000. Now he is a professor of China University of Petroleum(Beijing),and is mainly engaged in complex reservoir prediction and liquid detection.

Abstract

The shale gas resource is abundant in China,but the exploration level is relatively low.High-precision liquid detection method based on seismic data is critical as there is few well data.Based on the seismic elastic wave equation, the liquid mobility factor formula is deduced and the efficient exploration technique combined with high-precision time-frequency analysis algorithm is formed.The liquid mobility factor has a positive correlation with permeability,viscosity and density of reservoir. Based on the high-precision time-frequency analysis, the character of liquid is analysed,and the liquid mobility factor is calculated. Then, combined with well data, the range of factor in “sweet spot” area is guantified.The application in the Sichuan Basin demonstrates the precision and efficiency of the method as the result is consistent with the test data of well.This method will play a significant guiding role in shale gas exploration.

Key words: shale gas; liquid mobility factor; geophysical method; Sichuan Basin

Show Figures

1 概述

页岩气(shale gas)也称泥岩气, 是一种特殊的非常规天然气, 赋存于泥岩或页岩中, 具有自生自储、无气水界面、大面积连续成藏、低孔、低渗等特征。页岩气的研究始于美国, 中国对页岩气的研究从2003年起步。张金川等(2003)对页岩气的定义进行了简要论述; 张金川等(2004)完整地对页岩气的成藏机理进行了全面分析; 李武广等(2011)对页岩气的开发技术进行了综述, 但对地震勘探技术研究相对较少; 林建东等(2012)对页岩气的地震识别进行讨论, 采用的方法多为常规技术, 无针对性突破。基于Silin等(2004)提出的地震低频域饱和多孔介质储集层流体预测方法, 结合页岩气富集区地震频率特征, 作者将流体活动因子作为反映页岩含气性的一个重要标志, 首先采用高精度的时频分析方法对地震波场进行分离, 在确定气层与地震频率之间的关系后, 计算流体活动因子, 得到页岩气“ 甜点” 区的分布。

流体活动因子实质上反映的是地震资料中渗透性储集层与非渗透性储集层频谱的变化率。地震波在通过渗透性储集层时, 高频成分被储集层中的流体吸收, 低频能量相对加强, 频谱能量的相对集中使得频谱变化率出现正异常, 因此, 渗透性储集层的频谱变化率高于非渗透性储集层; 同理, 高频成分的衰减使得频谱能量在高频段分布均匀, 使得渗透性储集层的频谱变化率低于非渗透性储集层的频谱变化率。利用地震资料中渗透性储集层与非渗透性储集层频谱的变化率就可以获得流体活动性的变化量, 进而开展储集层储集性能和地层流体变化研究。在获得流体活动因子的过程中, 高精度的时频分析方法是决定流体活动因子分辨率的关键, 目前常规方法采用小波变换和广义S变换进行时频分析, 这两种方法由于受到测不准准则的制约, 计算精度明显降低, 作者采用的匹配追踪算法可以更好地适应信号的结构和特征, 有效地提高了时频分析的精确性, 进而提高了流体预测的准确性, 通过理论模型试算和在中国南方四川盆地的实际应用取得了明显的效果。

2 流体活动因子计算的方法和原理

2.1 流体活动因子的推导

通过引入渗流理论, Silin等(2004)在饱和流体多孔介质的研究中推导了一个的弹性波方程, 该方程可以描述地震波动力学特征, 又能把储集层的密度、渗透率与流体的黏度等油藏参数直接与地震传播特征联系起来。Silin等(2004)推导的弹性波方程可简化为:

$\begin{matrix} \{\begin{matrix} \frac{\partial^{2} u}{\partial t^{2}} + \frac{ρ_{f}}{ρ} \frac{\partial W}{\partial t} = v_{b}^{2} \frac{\partial^{2} u}{\partial x^{2}} - v_{f}^{2} \frac{\partial P}{\partial x} \\ λ_{f} \frac{\partial^{2} u}{\partial t^{2}} + W + τ \frac{\partial W}{\partial t} = - D \frac{\partial P}{\partial x} \\ \frac{\partial^{2} u}{\partial x \partial t} + \frac{\partial P}{\partial t} = - \frac{\partial W}{\partial x} \end{matrix} \end{matrix}$ (1)

其中, $\begin{matrix} v_{b}^{2} = \frac{1}{βρ}; v_{f}^{2} = \frac{1}{ϕ β_{f} ρ}; 压力扩散系数 D = \frac{κ}{ϕ β_{f} η}; λ_{f} = ρ_{f} \frac{κ}{η} 。 \end{matrix}$ 以分析沿X方向传播的平面简谐纵波为例来说明流体饱和多孔介质中地震波场的特征。设固体骨架位移、流体的达西速度和压力分别如下:

$\begin{matrix} u = U_{s} e^{i (wt - kx)}, \overset{̅}{u} = {\overset{̅}{U}}_{f} e^{i (wt - kx)}, P = P_{0} e^{i (wt - kx)} \end{matrix}$ (2)

将(2)中的平面纵波和流体压力表达式代入简化方程(1)中, 整理可得快纵波和慢纵波的低频域波场特征, 其形式分别如下:

$\begin{matrix} \{\begin{matrix} {\overset{̅}{U}}_{f}^{fast} \approx \frac{- εw (1 - γ_{ρ} γ_{v} - γ_{ρ})}{1 + γ_{ρ}} U_{s}^{fast} + \dots \\ {\overset{̅}{U}}_{f}^{slow} \approx - iw (1 + γ_{v}) U_{s}^{slow} + \dots \end{matrix} \end{matrix}$ (3)

其中, $\begin{matrix} γ_{v} = \frac{v_{b}^{2}}{v_{f}^{2}} = \frac{ϕ β_{f}}{β}; γ_{ρ} = \frac{ρ_{f}}{ρ}; ε = \frac{κρw}{η} 。 \end{matrix}$

接下来进行饱和流体多孔介质分界面的反射系数推导(Hampson et al., 2001; Goloshubin et al., 2002; Silin et al., 2004; 代双和等, 2010):

实际上, 地下介质一般具有层状结构, 因此需要讨论两种弹性性质不同的介质分界面上波的传播。设计地震反射模型, 上覆介质M1为理想的非渗透弹性介质, 下覆介质M2为饱和流体多孔介质, 如果平面纵波入射到介质的分界面, 则地震波应该满足以下边界条件:①位移、应力连续; ②由于上覆的弹性介质无渗透性, 因此, 在边界处流体的达西速度为零。边界条件如下:

$\begin{matrix} \{\begin{matrix} u_{1} |_{X = 0} = u_{2} |_{X = 0} \\ - \frac{1}{β_{1}} \frac{\partial u_{1}}{\partial x} |_{x = 0} = - \frac{1}{β_{2}} \frac{\partial u_{2}}{\partial x} |_{x = 0} + ϕp |_{x = 0} \\ {\overset{̅}{u}}_{f} |_{x = 0} = 0 \end{matrix} \end{matrix}$ (4)

其中, $\begin{matrix} u_{1} \end{matrix}$ 和 $\begin{matrix} u_{2} \end{matrix}$ 分别为M1与M2的固相位移。

在垂直入射的情况, 则介质M1中的垂直入射和反射的平面波可以表示为:

$\begin{matrix} u_{1} = U_{1} e^{i (wt - k_{1} x)} + R U_{1} e^{i (wt + k_{1} x)} \end{matrix}$ (5)

介质M2中的位移和压力分别为:

$\begin{matrix} \{\begin{matrix} p = \frac{1}{ϕ β_{f}} P_{0}^{s} e^{i (wt - k_{s} x)} + \frac{1}{ϕ β_{f}} P_{0}^{f} e^{i (wt - k_{f} x)} \\ u_{2} = U_{2}^{s} e^{i (wt - k_{s} x)} + U_{2}^{f} e^{i (wt - k_{f} x)} \end{matrix} \end{matrix}$ (6)

将式(3)、(5)和(6)代入边界条件(4), 整理后化简可以得到低频域反射系数的近似表达式, 形式为:

$\begin{matrix} R \approx \frac{A_{2} - A_{1}}{A_{2} + A_{1}} + B (v_{1}, v_{2}, ρ_{2}, κ, η) \sqrt[]{\frac{κρ}{η} w} \end{matrix}$ (7)

式中:A₁和A₂ 分别为上下介质的波阻抗, B是饱和流体多孔介质速度、密度、流体粘度等的函数, 与频率无关。

最后基于低频域反射系数推导流体活动因子:反射系数与储集层的渗透性、密度及流体黏度等油藏参数有关。令流体活动因子 $\begin{matrix} M \approx \frac{κρ}{η}, \end{matrix}$ 代入(7)式并对其进行角频率求导, 便可以得到流体活动因子的表达式, 形式如下:

$\begin{matrix} M \approx F (v, ρ, κ, η) \cdot {(\frac{\partial R}{\partial w})}^{2} * w \end{matrix}$ (8)

式中F为流体函数, 无量纲。

2.2 匹配追踪时频分析

常规时频分析方法一般采用广义S变换或小波变换作为时频分析工具, 效率较高但精度差, 文中采用匹配追踪时频分析方法:将地震信号在完备的时频原子库中自适应地分解为一组时频原子的线性组合, 尽可能精确地匹配原信号的局部结构, 准确表达信号的内部层次特征, 这样可以提高时频分析的精度, 进而完善流体活动因子的提取(黄捍东等, 2012)。这个过程是通过迭代完成的, 匹配分解在每一次迭代中提取最佳匹配子波 $\begin{matrix} m_{γ_{n}} \end{matrix}$ 。经过N次迭代后, 地震信号s(t)可以表示如下:

$\begin{matrix} s (t) = \overset{N - 1}{\sum_{n = 0}} a_{n} m_{γn} + R^{(N)} f \end{matrix}$ (9)

式中, a_n 是第n个子波 $m_{γ_{n}}$ 的振幅; R^(N)f是残差, 并且R⁽⁰⁾f=s(t)。

将信号分解后, 利用Wigner-Villa分布即可计算其时频谱:

$\begin{matrix} \begin{matrix} W_{m_{γ_{n}}} (t, f) = \frac{1}{2 π} \int_{-}^{\infty} m_{γ_{n}} (t + \frac{τ}{2}) \cdot m_{γ_{n}} (t - \frac{τ}{2}) \cdot \\ \exp (- i 2 πfτ) dτ = \sqrt[]{\frac{2 π}{β}} \frac{σ_{n}}{2 π f_{n}} \\ \exp (- (\frac{2 π^{2}}{β}) \frac{σ^{2} {(f - f_{n})}^{2}}{f_{n}^{2}}) \\ \exp (- (2 β) \frac{f_{n}^{2} {(t - τ_{n})}^{2}}{σ_{n}^{2}}) \end{matrix} \end{matrix}$ (10)

进而可以根据上式求得信号的时频谱为:

(11)

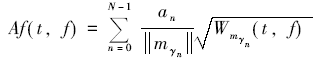
由于在低频域饱和流体多孔介质储集层中, 流体的活动性与反射系数对频率的偏导成正比, 而对实际地震记录来说, 可以近似地认为流体的活动性与反射振幅对频率偏导的绝对值成正比。这样利用匹配追踪获得的信号的时频谱就可以相应地计算并提取流体活动因子, 达到预测页岩气“ 甜点” 区的目的。

3 理论模型试算与实际应用

3.1 理论模型试算

设计理论模型进行试算以验证时频分析方法的精度。由于Morlet小波具有衰减特征, 与地震信号的子波具有相似性, 因此采用Morlet小波作为匹配分解原子, 可以避免直接求原始地震信号Wigner-Villa分布的交叉项干扰。

分两方面考察算法的适用性和精确性。设计如图1-a的理论信号(含随机噪声)进行匹配分解, 然后利用匹配分解的Morlet小波线性叠加得到的重构信号与其对比, 从残差可以看出理论信号与重构信号的波形匹配良好。图1-b为理论信号与重构信号在频谱上的对比, 可以看出, 重构之后的信号与理论信号的频谱信息也高度一致, 频谱分析也证实了信号的保真性, 基于Morlet小波的匹配分解的适用性得以验证。

	Figure Option View Download New Window
	图1 理论信号与重构信号对比分析 a— 理论信号与重构信号波形特征; b— 理论信号与重构信号的频谱特征Fig.1 Comparison of theoretical signal and reconstructed signal

为了验证匹配追踪算法对时频谱的分辨能力, 对图1-a中的理论信号分别利用GST(广义S变换)和MP(匹配追踪)算法分析它的时频谱变化特征。理论信号设计时在300 ms处为15 Hz和45 Hz的子波叠加, 600 ms附近存在30 Hz和40 Hz两个子波叠加, 如图2-b所示, 基于GST的时频分析在300 ms处, 分辨率有限, 且在600 ms处没有将2个子波完全分开, 可见虽然GST通过自适应的调节窗函数, 能较好地描述模型信号在时间和频率域的分布情况, 但精度必然受到测不准准则影响; 而MP算法不受测不准准则的制约, 无论在时间方向, 还是在频率方向都具有较高的分辨率(图 2-c)。

	Figure Option View Download New Window
	图2 理论信号不同算法的时频分析结果 a— 理论信号; b— GST算法时频谱; c— MP算法算法时频谱Fig.2 Results of different algorithm time-frequency analysis methods for theoretical signal

以上分析表明, 虽然GST和MP算法均能较精细地表征地震信号的时频谱分布特征, 但MP算法的精度相对较高, 并且具有一定的抗噪能力, 更适合定量分析地震信号时频特征。

3.2 实际应用

研究区位于中国四川盆地, 地质普查认为其页岩具有干酪根生烃、成岩作用以及构造应力产生裂缝的条件, 是页岩气富集的有利目标区。由于处于勘探早期, 钻井资料少、页岩气“ 甜点” 区不落实, 勘探风险较大。

基于研究区地震资料和地质分析结论, 应用时频分析技术对井旁地震道目的层志留系龙马溪组和五峰组进行谱分解, 分析页岩储集层频谱变化特征, 确定计算流体活动因子的频率范围; 再利用时频分析对地震记录逐道进行时频谱分解计算, 并沿目的层计算地震谱能量随频率变化的变化率, 提取流体活动因子; 最后, 结合测井和地震反演等数据, 综合分析流体活动因子, 建立识别含气储集层的模式, 预测页岩气“ 甜点” 区分布范围。

将流体活动因子剖面(图 3)预测的四川黔江地区志留系页岩气“ 甜点” 区位置与地震速度反演剖面(图 4)对比分析可以看出:速度反演剖面中(时间深度1700~1850, ms之间)两层低速页岩夹持的高速砂岩层与流体因子剖面上页岩气“ 甜点” 区发育的位置对应较好, 说明裂缝发育的脆性砂岩是页岩气聚集的有利场所, 预测结论与该地区地质认识一致。

	Figure Option View Download New Window
	图3 四川盆地志留系流体活动因子检测剖面Fig.3 Section of liquid mobility factor detection of the Silurian in Sichuan Basin

	Figure Option View Download New Window
	图4 四川盆地志留系反演速度剖面Fig.4 Velocity inversion section of the Silurian in Sichuan Basin

图5是位于四川盆地内一条过井地震剖面, 图6为对应的反演速度剖面。钻井过程中, 目的层志留系龙马溪组和五峰组钻遇两套黑色碳质页岩, 均有气测异常, 根据测井资料标定, 龙马溪组位于地震时间剖面530~550, ms之间, 五峰组位于560~580, ms之间, 且根据岩石物理统计规律, 页岩储集层速度分布在3900~4200 m/s之间, 从反演剖面上可清晰地见到两套稳定的低速层, 展现了页岩储集层广泛分布的特征。

	Figure Option View Download New Window
	图5 Z-1井过井地震剖面Fig.5 Seismic section crossing Well Z-1

	Figure Option View Download New Window
	图6 Z-1井过井反演速度剖面Fig.6 Velocity inversion section crossing Well Z-1

测井解释认为在两层碳质页岩储集层中, 井段785~802, m五峰组页岩为含气优质储集层, 完井测试在该井段获工业气流, 而龙马溪组页岩未获产量。图7为过井流体检测剖面, 图中页岩气“ 甜点” 区集中发育在五峰组, 龙马溪组未见流体响应, 与测试结论吻合。

	Figure Option View Download New Window
	图7 Z-1井过井流体活动因子检测剖面Fig.7 Liquid mobility factor section crossing Well Z-1

由此可见, 地震储集层反演可以较为准确地刻画出页岩储集层的分布, 但对页岩气“ 甜点” 的识别能力不足, 储集层只是流体聚集的必要条件。因此, 将储集层预测与流体检测成果共同应用有益于研究区页岩气的勘探。

4 结论

基于流体活动因子结合高精度时频分析方法进行页岩气“ 甜点” 区预测, 不受测井资料和构造层位的约束, 对勘探初期页岩气储集层含气情况的预测和识别具有重要的意义。通过理论模型试算和实际资料应用得到了以下认识:

1)流体活动因子利用含气储集层对地震波频率成分的影响进行流体检测, 可以有效确定页岩储集层中流体活动强烈的“ 甜点” 区;

2)高精度的时频分析方法是提高流体识别能力的关键, 匹配追踪法具有精度高、算法稳定的特点, 但计算效率较小波变换和广义S变换低;

3)流体活动因子的计算结果除了受方法的影响外, 地震资料的信噪比、分辨率等品质因素也是影响最终效果的关键, 因此, 高品质的地震资料对页岩气“ 甜点” 区的预测十分重要。

作者声明没有竞争性利益冲突.

参考文献

View Option

[1]	代双和, 陈志刚, 于京波, 等. 2010. 流体活动因子技术在KG油田储集层描述中的应用[J]. 石油勘探与开发, 37(5): 573-578. [文内引用:1]
[2]	黄捍东, 郭飞, 汪佳蓓, 等. 2012. 高精度地震时频谱分解方法及应用[J]. 石油地球物理勘探, 47(5): 773-780. [文内引用:1]
[3]	李武广, 杨胜来, 殷丹丹, 等. 2011. 页岩气开发技术与策略综述[J]. 天然气与石油, 29(1): 34-37, 7. [文内引用:1]
[4]	林建东, 任森林, 薛明喜, 等. 2012. 页岩气地震识别与预测技术[J]. 中国煤炭地质, 24(8): 56-60. [文内引用:1]
[5]	张金川, 金之钧, 袁明生. 2004. 页岩气成藏机理和分布[J]. 天然气工业, 24(7): 15-18. [文内引用:1]
[6]	张金川, 薛会, 张德明, 等. 2003. 页岩气及其成藏机理[J]. 现代地质, 17(4): 466. [文内引用:1]
[7]	Goloshubin G M, Korneev V A, Vingalov V A, et al. 2002. Seismic low-frequency effects from oil-saturated reservoir zones[R]. Salt Lake City: SEG Meeting. [文内引用:1]
[8]	Hampson D P, Schuelke J S, Quirein J A. 2001. Use of multiattribute transforms to predict log properties from seismic data[J]. Geophysics, 66: 220-236. [文内引用:1]
[9]	Silin D B, Korneev V A, Goloshubin G M, et al. 2004. A hydrologic view on Biot's theory of poroelasticity[A]. Paper LBNL-54459. [文内引用:4]
[10]	Valeri A K, Dmitry S, Valeri A K. 2006. Reservoir imaging using low frequencies of seismic reflections[J]. The Leading Edge, 83: 525-527. [文内引用:1]

2010

0.0

... 代双和等,2010): ...

2012

0.0

黄捍东, 郭飞, 汪佳蓓, 等. 2012. 高精度地震时频谱分解方法及应用[J]. 石油地球物理勘探, 47(5): 773-780.

由于受测不准准则的制约，应用小波变换、广义S变换等线性算法无法同时获得高时间分辨率和高频率分辨率，而应用匹配追踪算法可克服窗函数的限制，能在时间域和频率域同时精细表征信号特征。本文在阐述地震信号匹配追踪时频谱分解的算法原理基础上，通过对标准Morlet小波进行合理改造，完备了时频原子库，有利于提高地震信号匹配分解的精度；依据Morlet小波的时宽对地震道进行开时窗，可在多个时窗内同时动态扫描匹配小波原子，可以适当提高计算效率。模型试验与实际数据分析表明，基于改进Morlet小波的地震信号匹配追踪算法更精确更高效，且具备一定的抗噪能力，适合定量分析地震资料的频谱变化特征，有助于研究储层及油气的分布范围。

... 2 匹配追踪时频分析常规时频分析方法一般采用广义S变换或小波变换作为时频分析工具,效率较高但精度差,文中采用匹配追踪时频分析方法:将地震信号在完备的时频原子库中自适应地分解为一组时频原子的线性组合,尽可能精确地匹配原信号的局部结构,准确表达信号的内部层次特征,这样可以提高时频分析的精度,进而完善流体活动因子的提取(黄捍东等,2012) ...

2011

0.0

... 李武广等(2011)对页岩气的开发技术进行了综述,但对地震勘探技术研究相对较少 ...

2012

0.0

... 林建东等(2012)对页岩气的地震识别进行讨论,采用的方法多为常规技术,无针对性突破 ...

2004

0.0

张金川, 金之钧, 袁明生. 2004. 页岩气成藏机理和分布[J]. 天然气工业, 24(7): 15-18.

The reservoiring mechanism of shale gas is of the features of both the coalbedadsorbed methane and the conventionally trapped gas reservoirs，it showing a complicated multiplemechanism gradation character. In the reservoiring process of shale gas，the occurrence manner of the gas and the reservoiring type were gradually changed，and the abundance and enrichment degree of the gas were gradually increased. An whole process of the formation and evolution of shale gas reservoir may be divided into three stages，i.e. the absorption and accumulation stage，the expansion and cracking stage and the pistonlike driving or displacementlike migration stage. Relevant change in reservoiring condition and mechanism could control and influence the formation and distribution of shale gas reservoirs and the lithologic change and fracture development status played a control role in the occurrence and distribution of the gas in shale gas reservoir. The basic geological conditions of forming commercial shale gas reservoirs exist in many basins in China，in which Shuixigou Group in Tulufan Depression of Tuha Basin is one of the important horizons of shale gas generation.

1.China University of Geosciences; 2.Research Institute of Petroleum Exploration and Development，Sinopec; 3.Tuha Oil Field Branch Company

对页岩气成藏机理进行了全面分析，获得了四个方面的认识。①页岩气成藏机理兼具煤层吸附气和常规圈闭气藏特征，体现出了复杂的多机理递变特点。②在页岩气的成藏过程中，天然气的赋存方式和成藏类型逐渐改变，含气丰度和富集程度逐渐增加。③完整的页岩气成藏与演化可分为3个主要的作用过程，自身构成了从吸附聚集、膨胀造隙富集到活塞式推进或置换式运移的机理序列。④相应的成藏条件和成藏机理变化对页岩气的成藏与分布产生了控制和影响作用，岩性特征变化和裂缝发育状况对页岩气藏中天然气的赋存特征和分布规律具有控制作用。研究了我国的情况，认为我国的许多盆地存在工业性页岩气藏发育的基本地质条件，其中，吐哈盆地吐鲁番坳陷的水西沟群是页岩气发育的重要区域之一。

... 张金川等(2004)完整地对页岩气的成藏机理进行了全面分析 ...

2003

0.0

... 张金川等(2003)对页岩气的定义进行了简要论述 ...

2002

0.0

... Goloshubin et al ...

2001

0.0

... 接下来进行饱和流体多孔介质分界面的反射系数推导(Hampson et al ...

2004

0.0

... 基于Silin等(2004)提出的地震低频域饱和多孔介质储集层流体预测方法,结合页岩气富集区地震频率特征,作者将流体活动因子作为反映页岩含气性的一个重要标志,首先采用高精度的时频分析方法对地震波场进行分离,在确定气层与地震频率之间的关系后,计算流体活动因子,得到页岩气#cod#x0201c ...

... 1 流体活动因子的推导通过引入渗流理论,Silin等(2004)在饱和流体多孔介质的研究中推导了一个的弹性波方程,该方程可以描述地震波动力学特征,又能把储集层的密度、渗透率与流体的黏度等油藏参数直接与地震传播特征联系起来 ...

... Silin等(2004)推导的弹性波方程可简化为: ...

... Silin et al ...

2006

0.0