庄陈程, 战庆, 王张华. (2014)利用长江口现代潮滩沉积硅藻建立海平面转换函数的尝试[J]. 古地理学报, 16(4): 557-568
Zhuang Chencheng, Zhan Qing, Wang Zhanghua. (2014)An attempt on construction of diatom-based sea-level transfer functions in modern tidal flat at Yangtze River estuary[J]. Journal Of Palaeogeography, 16(4): 557-568. DOI:10.7605/gdlxb.2014.04.046  
Permissions
Copyright©2014, 《古地理学报》编辑部
版权所有.《古地理学报》编辑部
利用长江口现代潮滩沉积硅藻建立海平面转换函数的尝试
庄陈程1, 战庆2, 王张华3
1 华东师范大学资源与环境科学学院,上海 200062
2 上海市地质调查研究院,上海 200072
3 华东师范大学河口海岸国家重点实验室,上海 200062

通讯作者简介 王张华,女,1973年生,博士,教授,主要研究方向为河口三角洲沉积地貌环境演变。E-mail:zhwang@geo.ecnu.edu.cn。

第一作者简介 庄陈程,男,1986年生,硕士研究生,主要从事定量海平面重建研究。E-mail:zhuangchen2000@163.com。

收稿日期:2012-03-06
基金:国家自然科学基金项目(编号:41176070)和河口海岸国家重点实验室自主课题资助
摘要

在高精度海平面定量重建研究中,有孔虫、硅藻等海洋微体古生物转换函数技术是近 10余年随着计算机技术发展而快速兴起的一项新技术,已成为欧美地区研究海平面变化的不可或缺的定量手段之一,而其在中国沿海地区全新世海平面定量重建中的应用却屈指可数。以硅藻为例,详细介绍了建立其与海平面之间的转换函数的过程,包括现代表层样采集、统计学分析、误差的可能来源和减小误差的方法。通过在对崇明岛四滧港 SY剖面潮滩表层样品的环境因子分析和对硅藻属种的 CCA排序分析发现,高程对潮滩硅藻属种排序有着很高的解释贡献。随后通过 WA和 WA-PLS建立模型,四滧港 SY剖面全样 WA-PLS模型的相关系数(R 2_Jack)达到 0.9004,预期误差( RMSEP)为 12.622,若不考虑潮上带样品 SY1后的转换模型其精度更能达到 ±10 cm。本研究以期带动此项技术在国内的发展,促进高精度海平面定量重建,从而能为沿海地区海岸带管理提供更详实、更具现实指导意义的地质记录。

关键词: 微古化石; 硅藻; 海平面重建; 转换函数; 长江口
中图分类号:P736.22+1 文献标志码:A 文章编号:1671-1505(2014)04-0557-12
An attempt on construction of diatom-based sea-level transfer functions in modern tidal flat at Yangtze River estuary
Zhuang Chencheng1, Zhan Qing2, Wang Zhanghua3
1 College of Resources and Environmental Science,East China Normal University,Shanghai 200062
2 Shanghai Institute of Geological Survey, Shanghai 200072
3 State Key Laboratory of Estuarine and Coastal Research,East China Normal University,Shanghai 200062

About the corresponding author Wang Zhanghua,born in 1973,is a professor of East China Normal University. She is mainly engaged in research on sedimentary geomorphologic evolution of estuary and delta. E-mail: zhwang@geo.ecnu.edu.cn.

About the first author Zhuang Chencheng,born in 1986,is a postgraduate of East China Normal University(Shanghai). Now he is engaged in research on quantitative sea-level reconstruction. E-mail:zhuangchen2000@163.com.

Abstract

In the research on quantitative high-resolution sea-level reconstruction,microfossil-based transfer function is a newly and rapidly developed technique assisted by the development of computer technology in the past decade. It has become one of the indispensable methods in sea-level research in many western countries. However,its application to reconstructions of the Holocene relative sea-level history in Chinese coasts has been limited. This paper intends to introduce the method of the diatom(as an example)based sea-level transfer functions,including tidal flat sampling strategy,statistical analysis, possible prediction errors and reducing-error method. Through analyzing the tidal flat surface samples collected from SY section at Siyao port of Chongming Island and the CCA ordination of diatom species,it was concluded that the elevation is the most contributing factor for diatoms sorting among all the environmental parameters. Thus,a transfer function with weighted average(WA)and weighted average partial least squares(WA-PLS) was used. The correlation( R2_Jack)is 0.9 and the RMSEP is±12.6 cm with all samples of SY section at Siyao port. The precision may be improved to ±10 cm when the sample from a supratidal site(sample of SY1)is excluded. This research will push such quantitative methods forwards to a higher level in high-resolution sea-level reconstructions that can help produce high-quality geological records to aid coastal management of China.

Key words: microfossil; diatoms; sea-level reconstruction; transfer function; Yangtze River estuary
1 概述

海平面指示着海水容量和全球洋流的变化, 其变化对海洋大气系统和人类活动有着重要的影响。作为河口海岸带古地理及古环境研究的最重要问题, 区域相对海平面变化曲线一直是研究工作的重要组成部分。进入20世纪后, 随着全球变化和区域响应联动机制逐步被深入探讨和认识, 特别是全球变暖和海平面加速上升对人类社会经济发展造成了威胁, 使得古海平面的变化趋势尤其是末次冰消期以来的海平面变化方面的研究变得愈发重要和迫切。

微体古生物化石转换函数定量重建古地理环境和海平面是一项自20世纪70年代发展起来的新技术。早在1971年, 美国学者就利用一组钻孔顶部样品的有孔虫数据, 结合因子分析和多元回归分析2种统计学的方法, 建立了一套海水温度与有孔虫组合的定量对应关系, 再将其反推到钻孔中从而得到定量的古海水温度数据(Imbrie and Kipp, 1971)。这种方法在20世纪70年代著名的CLIMAP(“ 气候长期调查制图与预报” )计划中起着至关重要的作用, 共4个门类11项转换函数被用来重建末次盛冰期以来的全球古海洋和古气候格局。后来, 这种方法被广泛地应用到钙质超微化石(Geitzenauer et al., 1976)、放射虫(Sachs, 1973)、硅藻(Zong and Horton, 1999)、有壳变形虫(Charman et al., 2010)和介形虫(Frenzel et al., 2010)等海洋微体化石, 以求得古地理环境的定量数据。虽然转换函数早在20世纪70年代初就应运而生, 但是直到20多年后这种精确的定量方法才被应用到重建海平面的研究(Guilbault et al., 1995; Horton et al., 1999; Zong and Horton, 1999), 在最近10来年, 该海平面定量重建方法在欧洲、日本和北美已得到广泛有效的应用(Zong and Horton, 1999; Edwards et al., 2004a; Sawai et al., 2004; Horton et al., 2006; Leorri et al., 2008; Hawkes et al., 2010)。

相比定性及半定量的沉积相与地层学的研究, 这种定量方法在对晚全新世, 尤其是近数百年来由于地壳活动所造成的相对海平面波动事件的研究上有明显优越性。以1700年北美卡斯卡蒂大地震对北美西海岸俄勒冈州的几大河口造成的沉降为例(表 1), 通过建立现代微古化石并运用到钻孔中取得过去数百年的海平面波动曲线, 其分辨率可达分米甚至厘米。虽然在实际的运用过程中, 由于钻孔位置不理想、地层受侵蚀而缺失或者表层属种和地层难以类比等问题可能对最后重建结果造成一定的偏差, 但是, 总体而言, 转换函数所推算的结果比一般定性分析要精确和可信得多。

表1 美国俄勒冈州5个河口区在1700年大地震时的沉降量(即相对海平面上升量) Table1 Subsidence amplitude of five estuaries in Oregon, USA, at 1700 AD earthquake

通过转换函数来研究海平面波动的技术在欧美等发达国家和日本都已经非常成熟, 但是在中国沿海地区却还未见类似报道。中国对转换函数的尝试始于1988年对南海13 000 a以来冬夏表层海水平均温度的再现(王律江和汪品先, 1986)。此后, 一些中国学者在其他方面也对转换函数定量研究做了些可行性尝试, 如利用某些孢粉对气候敏感的特性建立反映古气候的转换函数(宋长青等, 1997; 李珍等, 2002; 陈星等, 2008); 通过建立硅藻— pH值转换函数来研究长江中下游湖泊的富营养化过程等(董旭辉等, 2006), 都取得了不错的效果。而应用此法来探讨中国沿海地区全新世海平面波动的研究几乎空白, 该方法在中国淡水径流量丰富的大河口是否适用, 值得深入展开。因此, 作者利用长江口崇明岛潮滩湿地采集的表层沉积物, 通过鉴定硅藻属种和高程测量, 初步尝试了建立硅藻— 海平面转换函数的可行性, 研究结果不仅可促进定量重建长江口高分辨率的全新世相对海平面曲线, 同时也有助于今后包括台风、风暴潮和地震等事件造成的相对海平面快速上升的定量研究, 从而能为沿海地区海岸带管理提供更详实、更具现实指导意义的地质记录。

2 材料和方法
2.1 样品采集及处理

在采集现代表层样品的选址方面, 考虑到上海周边地区高潮滩围垦剧烈的实际情况, 所以选定多数高潮滩仍处于自然淤涨的崇明岛作为首选采样地区。崇明岛南岸受涨潮流作用, 侵蚀明显, 潮滩发育较差, 而且淡水径流强烈, 盐度低且变化幅度小, 与全新世海侵地层较难类比; 崇明东滩为鸟类湿地保护区, 且滩涂过于宽阔(最宽处达十几千米), 采样难度太大。因此最终于2010年7月中旬选择崇明岛北部四滧港东侧的滩涂(N31° 37'25″、E121° 45'10″)作为采样地点(图 1)。SY剖面长约450 m, 沿着剖面植被带的变化从芦苇带到光滩共采集17个表层样品(图 2)。采集的样品分为两部分, 包括5 cm× 5 cm表层1 cm厚淤泥用于硅藻分析, 以及10 cm× 10 cm的表层1 cm厚淤泥用于测量影响硅藻分布的环境因子, 包括粒度、有机碳等。同时用便携式盐度计和酸度计测量孔隙水中的其他2个可能影响硅藻生长的环境因子— — 盐度和pH值; 并用TOPCON全站仪记录下每个采样点的相对高程, 最后通过上海市测绘院编号为10-284的高程控制点(图 1)将采样点的相对高程转化为黄海高程。其中SY1号样品位于平均大潮线之上, 土质较干, 无法采得孔隙水, 因此盐度和pH值数据空缺, 其余样品数据完整。

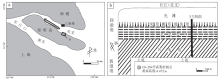图1 长江口四滧港SY剖面位置(a)和植被分布(b)示意图Fig.1 Sketch showing location (a) and vegetation distribution (b) of SY section at Siyao port, Yangtze River estuary

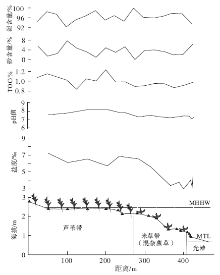图2 四滧港SY剖面环境因子、植被变化及采样位置示意图Fig.2 Sketch showing environmental factors, vegetation distribution and sample positions of SY section at Siyao port

在实验室处理的过程中, TOC用Elementar元素分析仪测定; 粒度用激光粒度仪来测定, 其中小于63 μ m的为泥样, 大于63 μ m则为沙样, 并用累积百分比表示; 所有硅藻样品的处理均依据Hå kansson(1984)方法进行, 主要处理步骤如下:(1)去除钙质。在装有硅藻样品的试管中加入浓度为10%~15%的稀盐酸, 待样品与盐酸初步反应后搅拌均匀并静置12 h以上, 然后用蒸馏水清洗3次。(2)去除有机质。加入浓度为30%的双氧水, 待样品与双氧水初步反应后, 置于恒温(约70 ℃)水浴锅中加热1~2 h, 其后将样品用蒸馏水清洗3次。(3)制成样片。用玻璃棒将样品均匀涂于载玻片上, 滴上Naphrax胶(dn=1.73), 盖上盖玻片, 然后在电热板上加热至150~200 ℃, 待气泡排出后冷却, 保存于样品盒中。硅藻鉴定与计数均在1000倍尼康E200油镜下进行, 每个样品统计硅藻壳面数至少200个, 用丰度百分比来表示各属种相对含量。大部分硅藻鉴定到种, 少数到属。鉴定过程主要依据金德祥等(1982, 1991)等专著, 以及王开发等(2001)、闵华明和马家海(2007)等文献资料。

2.2 数据标准化处理

首先, 需要建立现代表层样的硅藻属种数据库, 因此, 把在任意一个样品中出现的、且含量大于3%的硅藻属种作为研究的对象(Zong and Horton, 1999)。硅藻壳体完整度在1/2以上的才会被计数在内, 而直链藻属(Melosira)等无论长短都按一个单独个体来统计。10 μ m以下的微型底栖硅藻如舟形藻属(Navicula)和菱形藻属(Nitzschia)等种类繁多、个体微小, 且在1000倍油镜下难以准确命名, 故不在此次统计范围之内。选取盐度、pH值、TOC、高程和粒度等5个环境因子作为可能影响硅藻生长的因素。除高程之外的其他指标均不为负值或微量值, 因此不必用log函数进行标准化转化(Lepš and Š milauer, 2003)。由于不同的潮滩或河口地区潮水位、潮差不同, 因此需将现代表层样品的高程根据潮水位进行标准化, 即根据采样地点当地的平均高高潮(MHHW)和平均潮(MTL)的水位数据来计算出一个标准海平面指数(SWLI), 以此来统一样品的高程参数, 使采自不同潮滩的数据可以在一个相同的框架下使用和运算(Zong and Horton, 1999; Hamilton and Shennan, 2005a; Leorri et al., 2008; Hawkes et al., 2011)。采集的样品虽然来自同一个潮滩, 但为了和今后采自其他地点潮滩样品的数据具有可对比性和进一步运算, 也需要高程数据标准化。第n号样品的标准海平面指数SWLIn用公式可表达为:

SWLIn=100(hn-hMTL)/(hMHHW-hMTL)+100

其中hn表示第n号样品的地面高程, hMTL表示该采样点的平均潮水位高程, hMHHW代表了平均高高潮水位高程。考虑到有些采样点的高程值为负数, 一般会在公式中加上常数100(也可以是200或更高)(Zong and Horton, 1999), 因此平均潮水位和平均高高潮水位的样品的SWLI值就分别为正整数100和200, 从而便于之后的图件制作和分析计算。最后再通过逆运算把该标准海平面指数换算成当地基准标高。文中潮水位值根据实测剖面的地形和植被带变化, 并参考长江口北支北岸的南通3条港验潮站(图 1-a)水文数据, MTL和MHHW分别为0.69 m和2.19 m(图 2), 经过换算可得1个单位SWLI约为1.5 cm。

2.3 典型对应分析(CCA)

CCA是基于生态学理论的一种梯度分析和加权平均回归方法, 能将属种、样点及环境指标之间的关系反映在坐标轴上, 而所有坐标轴都限制为环境变量的线性组合, 同时假定该生物种类对环境的单峰响应特点, 即该生物沿环境变量梯度呈中心分布而非线性分布(ter Braak, 1987, 1996)。典型对应分析的常规分析主要按照以下步骤进行:(1)由反趋势对应分析(Detrended Correspondence Analysis, DCA)得出属种的单峰响应值(梯度长度SD), 当SD的数值大于2时, 即可进行CCA分析。(2)用partial CCA法测试各环境变量的边界效应, 即每次只包含1个环境变量作为CCA分析的主变量, 而其余变量则成为携变量。运用此法可以测试单个环境变量对藻类的影响, 即所谓的边界效应(Marginal effect)。(3)环境变量的重要性按照其单独解释属种数据的方差值的大小排出顺序, 其解释的显著性由蒙特卡洛测试(Monte Carlo Permutation Test)来检验, 其中显著性p< 0.05, 最重要且显著的变量(即有最大的边界和独立效应)用于建立转换函数模型(ter Braak, 1986)。(4)最后用反趋势典型对应分析(DCCA)来判识数据库是否适用于非线性或线性回归模型的建立。DCCA分析中每次只限定一个环境变量, 根据环境变量在第1轴上的有效梯度长度, 来判识硅藻对该变量的响应模式。当梯度长度不小于2个标准离差单元时, 可以用非线性加权平均模型来建立硅藻— 环境指标转换函数; 反之用线性模型比较适合(ter Braak and Juggins, 1993; Birks, 1995)。最后将生成的扩展名为sol的数据文件, 应用CANODRAW做出物种— 环境因子关系的双序图。以上各项分析均可通过Canoco软件4.5版本来实现(ter Braak and Š milauer, 2002)。

2.4 建立转换函数

转换函数的建立和检验都将通过功能更强大的C2软件来进行(Juggins, 2003)。一般而言每一种生物与环境变量之间并非单纯的线性关系, 而是在大多数情况下一种生物种类沿环境变量梯度呈中心式分布, 即如果某一生物离开了最适宜生长的特定环境区间, 其数量明显减少, 甚至会无法生存(ter Braak, 1996)。对于非线性响应模式主要用到加权平均回归法(WA), 由于在计算中对初始值进行了2次加权导致其变小, 为了得到准确的推导值需将其还原, 根据还原方式的不同和对属种忍耐值的降权与否可以分为传统加权平均(WA_Cla)和反向加权平均(WA_Inv); 以及对属种忍耐值降权的传统加权平均(WAtol_Cla)和反向加权平均(WAtol_Inv)。另外一种较为复杂的方法则是目前最主流的偏最小二乘加权平均回归法(WA-PLS)。WA-PLS是在加权平均回归的基础上, 对前一个函数残余的信息量进行多次提取和优化从而达到提高转换函数推导能力的目的(ter Braak and Juggins, 1993)。相比之下WA无论在理论概念上还是计算上都相对比较简单, 而WA-PLS则可以算作是WA方法的优化和递进。

转换函数的推导能力主要靠预测均方根差(RMSEP)以及相关系数(R2_Jack)来衡量。前者指示了该转换函数的实际推导预测误差, 其数值越低则函数推导能力越强, 在运算过程中其单位始终为SWLI; 后者指示了模拟值与实测值之间的拟合度, 其数值越高则函数推导能力越强。为了能够准确评估转换函数的推导能力, 通常又采用交互检验(Cross Validation)来经行误差检验。C2软件中自带Leave-One-Out(LOO)、n-fold cross validation和Bootstrap等3种交互检验的模型可供选择。文中将采用C2软件自带的LOO(也称Jack-knifing)来进行检验计算, 即用每个样本单独作为1次测试集, 剩余n-1个样本作为训练集来建立模型, 故1次LOO检验(LOOCV)共要建立n个模型。虽然这种方法相较于其他检验法更为麻烦, 但它最接近母体样本的分布, 估测所得的归纳误差比较可靠。

3 研究结果
3.1 环境因子及硅藻属种分布

从采样现场用手持酸度计和盐度计实测孔隙水中酸度和盐度的情况来看, 潮滩的酸度总体偏弱碱性, 但是梯度变化不大, 基本在7~8之间波动。孔隙水盐度从高潮滩芦苇带较高, 为7‰ 左右, 米草带显著下降, 为3‰ ~4‰ , 到光滩又略有上升, 为4‰ ~5‰ (图 2)。剖面的TOC含量较低且变化较小, 芦苇带较高, 多为1.0%~1.2%, 米草带和光滩较低, 为1%上下。粒度分析显示SY剖面潮滩表层沉积物粒径较细, 样品63 μ m以下的泥质成分都在92%以上, 个别样品甚至达到了99%, 而且, 从芦苇带到光滩, 泥的含量没有明显的分带性(图 2)。

硅藻鉴定结果显示, 崇明岛北部四滧港SY剖面表层沉积物的硅藻含量比较丰富, 17个样品中共统计到硅藻19属58种, 绝大部分是底栖种, 浮游种零星出现。其中高潮滩芦苇带的优势种为Achnanthes brevipes var. angustata, Nitzschia granulata(图 3); 中潮滩米草、海三棱藨草共生带的优势种为Raphoneis amphiceros, Cyclotella meneghiniana, Frustulia vulgaris; 光滩的优势种则为Navicula scopulorum, Gyrosima spencerii, Frustulia rombodies。SY1样品中以Nitzschia obtusa var. scalpelliformis占绝对优势, 却与高潮滩芦苇带其他样品的优势种组成有所不同; 故在之后建立模型时, 将会分别讨论包括SY1样品与否及其对模型推导能力的影响等问题。

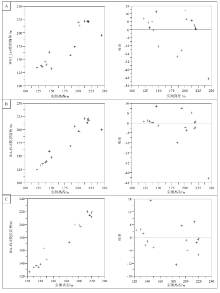
图3 四滧港SY剖面硅藻优势属种百分比浓度分布Fig.3 Distribution of percentage of advantaged diatom species of SY section at Siyao port

3.2 CCA分析结果

文中采用的环境变量为国际上常用的高程、盐度、pH值、粒度、TOC等(Zong and Horton, 1999; Sawai et al., 2004)。通过对原始藻类数据的DCA 分析, 第1、2轴的特征值分别是0.618和0.269, 解释的属种数据的方差值分别是42.3%和18.4%, 其中第1轴的特征值明显高于第2轴, 表明藻类的属种分布主要由第1轴的环境因子所解释。另外本次测试的属种分布的梯度长度SD值为2.807, 则表明该组硅藻数据相对于第1、2轴具有明显的单峰模型响应关系, 即可以用典型对应分析(CCA)来分析藻类与环境之间的关系。硅藻属种与环境变量的CCA分析结果(图 4), 较好地反映了硅藻种类的分布和各环境特征的相关性, 从中可以明显看出藻类的种类分布与高程、pH值、盐度、TOC和粒径等都具有一定的关系。其中高程和TOC这2种指标与第1轴联系紧密, 而盐度和pH值指标则与第2轴较为相关。从表2的具体数据来看, 两主要轴(轴1和轴2)的特征值分别为0.556和0.158, 累计反映了83.1%的硅藻属种与环境之间的关系。这些解释变量共解释了该剖面58.9%的硅藻属种变化, 另外41%仍然无法解释(图 5-A), 但是确已经足够说明硅藻与第1、第2两轴所代表的高程和pH值等之间的联系。而进一步通过单个变量的Partial CCA分析研究显示, 在已解释的部分中, 高程占据了23%, 远远高于其他环境因子, 分别为盐度8%、pH值10%、TOC值7%, 粒度5%(图 5-B)。与之相关的蒙特卡洛检验也表明这些环境变量能够在一定程度上解释该组硅藻数据的变化。因此, 统计意义上的硅藻组群和高程之间的定量转换函数是能够被建立的。但是在被解释的部分中仍然有47%的部分属于各环境变量之间的组间相关性(图 5-B), 高程转换函数并不完全独立于其他几个环境变量之外。关于41%无法解释的部分(图 5-A), 很大程度上可能是季节性差异导致(Horton and Edward, 2003), 也有可能是一些统计意义上模棱两可的随机性。

图4 28个含量不小于3%的硅藻属种与各环境变量CCA双轴图 (每个三角代表了1个属种)Fig.4 CCA biplots of diatom species-environment with 28 species with content above 3%(every triangle represents a specie)

表2 CCA分析结果总结 Table2 Summary of CCA ordination

图5 解释变量对硅藻群组的解释量、未解释量百分比(A)和各个环境变量对硅藻群组的解释百分比(B)Fig.5 Pie charts showing total variation(%)of diatoms species in explained and unexplained portion(A) and unique contribution of each environmental factors(B)

3.3 转换函数的建立

通过Canoco软件对样本进行DCCA分析可以得到第1轴的梯度长度为2.633个单位, 符合大于2.4个标准离差单元的单峰响应临界, 因此采用非线性加权平均模型WA和WA-PLS来建立硅藻— 高程指标转换函数, 并且根据观测值和预测值之间的RMSEP和R2_Jack来尝试比较分析哪套模型更加有说服力, 其中WA模型和WA-PLS的模型1包含了该组全部17个样品中浓度大于3%共28个属种的硅藻数据, 而模型2则把其中回归误差较大的SY1号样品去除, C2最后输出结果报告如表3所示。通常情况下, 反向回归模型比传统回归模型整体推导误差更低, 而传统回归模型则更侧重于某个区间内推导值与实测值之间的符合程度(ter Braak and Juggins, 1993)。因此在4个WA模型中, 对忍耐值不降权的反向加权平均回归(WAtol_Inv)具有最高的相关系数和最小的预测偏差(图 6-A)。WA-PLS转换函数模型的结果包括了5个组分, 从表3的数值列表中可以明显看出, 经过残差成分提取的WA-PLS模型明显比WA模型具有更小的均方根差和更高的相关系数, 从而使得WA-PLS转换函数的推导能力更强。在全部样品的情况下, 组分5的R2_Jack为0.9004, 而RMSEP为12.622个单位的SWLI, 比其他4组更具有推导表现力(表 3)。当去除了潮上带样品SY1后, 该转换函数的表现能力进一步得到提升, 其中组分4的表现结果最好, 其R2_Jack为0.96719, 比原来提高了7.4%; 而RMSEP降到了6.6767, 比原来降低了47.1%; 而且另一个判断函数推导能力的重要指标— 最大偏差(MaxBias_Jack)也从原来的44.391骤降至12.653(表 3)。综上所示, 模型2的组分4是最理想的模型。

图6 长江口四滧港SY剖面WAtol_Inv(A), WA-PLS模型1组分5(B)和模型2组分4(C)3个硅藻— SWLI转换函数实测值与推导值的拟合及残差Fig.6 Observed and predicted values of SWLI and their residual errors for WAtol-Inv(A), model 1(component 5)(B) and model 2(component 4)(C)of SY section at Siyao port, Yangtze River estuary

表3 长江口四滧港SY剖面硅藻— 高程多种转换函数检验结果比较 Table3 Statistics summary of every diatom-SWLI transfer function of SY section at Siyao port, Yangtze River estuary
4 讨论和结论

长江口崇明岛发育着广阔的盐沼和潮滩, 在这个特殊环境中, 由于高程控制着潮水淹没的时间和频率, 从而造成现代盐沼— 潮滩的各种环境特征和参数均有明显的水平分带现象。遵照“ 现代是过去的钥匙” 原则, 通过地层沉积物的垂向分布和利用现代潮滩沉积建立的转换函数, 就可以恢复过去的海平面波动过程。文中的分析结果表明, 利用长江口现代潮滩硅藻属种建立高程转换函数是可行的。夏季水温较高且日光充足, 使得硅藻的光合作用加强, 硅藻大量繁殖。因此四滧港SY剖面潮滩不同地貌单元沉积物中硅藻数量均足够丰富, 如闵华明和马家海(2007)的研究显示每平方米硅藻数量平均可达7.0× 106 cells。而且各单元都有特定的优势属种(图 3), 分带性明显, 比分布不均、呈簇状分布的有孔虫更具优势(吉云松, 2004)。

CCA分析和偏CCA分析表明在用于解释的环境变量中, 高程参数SWLI与硅藻组合之间的相关性最为密切的, 占总解释量的23%。虽然图5-B显示, pH值解释了10%的硅藻变化率, 说明是另一个潜在的可以进行定量重建的环境指标。不过, 该潮滩剖面的pH值变化范围很小(图 2), 没有明显的环境梯度变化, 因此并不适合用来建立转换函数。盐度是影响硅藻分布最为密切的因素之一(图 4; 图5-B), 利用盐度来反演过去海水盐度波动的研究在国外也屡见不鲜(Fritz et al., 1991; Hassan et al., 2009; Zong et al., 2010)。但在本研究中虽然盐度也对硅藻分布的解释有约8%的贡献, 但是蒙特卡洛检验显示p=0.138的显著性并不适合用以建立转换函数, 这可能与SY剖面的盐度分布特征有关, 即盐度并不是随高程的减小而增高, 反而是高潮滩盐度较高、米草带最低、光滩略有上升(图 2)。TOC也是可能影响硅藻分布的一个环境指标, 本次研究TOC具7%的解释贡献率, 但p=0.374的显著性检验结果也说明它不适合建立转换函数。分析原因可能是研究区陆源碎屑物供应丰富、沉积速率高, 从而导致盐沼区TOC偏低; 另外光滩虽然没有植被生长, 但潮流往往带来丰富的植物残体、碎屑, 因此和高、中潮滩TOC含量差异不显著(图 2)。前人研究也显示长江口全新世钻孔沉积物的TOC含量较低, 一般小于1%(王华新等, 2011)。

在建立转换函数方面, WA-PLS回归模型的第1组分的数值基本上是与WA的结果保持一致的, 通过对第1组分中的剩余相关进行优化和重新计算从而生成了第2组分, 依此类推此后每一个组分都是对前一组分的修正和改进, 从某种程度来说, WA-PLS就是WA的一种衍伸和发展(ter Braak and Juggins, 1993; Birks, 1995)。从表3可以很明显地看出, WA-PLS所建立的转换函数比WA的具有更高的相关系数和更小的预测均方根差, 因此用WA-PLS所建立的硅藻— 高程转换函数普遍比传统的回归模型具有更强的推导能力(图 6-A, 6-B)。可以看到在包括SY1样品的模型1中, 预期误差在12.6个SWLI单位左右, 换算成高度单位是± 19 cm。在没有用到SY1样品所建立的模型2中, 其推导能力大幅提高, 其预期误差在6.7个SWLI单位左右(表 3), 换算成长度单位为± 10 cm。相比较在世界其他地区所建立的海平面模型, 如Zong和Horton(1999)在英国6个河口地区利用硅藻建立的海平面转换函数, 其精度为± 25 cm; Sawai等(2004)在日本数河口同样基于硅藻建立的海平面转换函数, 其精度在± 29 cm; Horton等(2006)在美国北卡罗来纳州的河口也是通过硅藻所建立的转换函数, 其精度达到了± 8 cm, 文中的模型的精确程度还是非常理想的。

本次研究只是对长江口硅藻— 高程转换函数可行性的初步尝试, 还不能运用到本区和其他沿海区域的全新世钻孔沉积物, 因为此次建立的现代表层沉积物的分布范围有限, 采样季节也仅限于洪季, 不能代表整个长江口的硅藻分布, 也可能难和全新世沉积物中的硅藻化石进行良好的类比。若想建立一个能适用于整个长江三角洲地区的转换函数的话, 将沿海盐沼现代表层硅藻数据库向北扩展至江苏南通沿海、向南至南汇嘴及杭州湾北岸也是十分必要的。在建立了完整可靠的现代表层数据库之后, 于合适的位置采得一套连续、完整和高分辨率的全新世沉积物样品也是十分重要的。此外如何能从钻孔中测得精确的年代数据也是决定反演精确与否的一个重要因素。在百年尺度的反演过程中, 将理论中反演数据与验潮站的实测数据进行比对则更能提高转换函数的推导能力。

参考文献
1 陈星, 朱诚, 马春梅. 2008. 气候转换函数中孢粉因子的气候敏感性分析[J]. 科学通报, 53(增刊Ⅰ): 45-51. [文内引用:1]
2 董旭辉, 羊向东, 王荣. 2006. 长江中下游地区湖泊硅藻—总磷转换函数[J]. 湖泊科学, 18(1): 1-12. [文内引用:1]
3 吉云松. 2004. 利用有孔虫建立高精度海平面变化标尺[D]. 上海: 华东师范大学硕士学位论文. [文内引用:1]
4 金德祥, 程兆第, 刘师成, 等. 1982. 中国海洋底栖硅藻类(上卷)[M]. 北京: 海洋出版社. [文内引用:1]
5 金德祥, 程兆第, 刘师成, 等. 1991. 中国海洋底栖硅藻类(下卷)[M]. 北京: 海洋出版社. [文内引用:1]
6 李珍, 王开发, 王永吉. 2002. 红树林孢粉—气候因子转换函数恢复古环境的可行性初探[J]. 海洋科学进展, 20(3): 73-78. [文内引用:1]
7 闵华明, 马家海. 2007. 上海市滩涂夏季底栖硅藻初步研究[J]. 热带亚热带植物学报, 15(5): 390-398. [文内引用:1]
8 宋长青, 吕厚远, 孙湘君. 1997. 中国北方花粉—气候因子转换函数建立及应用[J]. 科学通报, 42(20): 2182-2185. [文内引用:1]
9 王华新, 线薇微. 2011. 长江口表层沉积物有机碳分布及其影响因素[J]. 海洋科学, 35(5): 24-31. [文内引用:1]
10 王开发, 蒋辉, 支崇远, 等. 2001. 东海表层沉积硅藻组合与环境关系研究[J]. 微体古生物学报, 18(4): 379-384. [文内引用:1]
11 王律江, 汪品先. 1988. 用转换函数法推算南海古温度的尝试[J]. 科学通报, 33(5): 371-373. [文内引用:1]
12 Birks H J B. 1995. Quantitative palaeoenvironmental reconstructions[A]. In: Maddy D, Brew J S(eds). Statistical Modelling of Quaternary Science Data[C]. UK: Cambridge University Press, 161-236. [文内引用:2]
13 Briggs G G. 1994. Coastal Crossing of the Zero-Isobase, Cascadia Margin, Southcentral Oregon Coast Masters Thesis[M]. Portland : Portland State University: 1-251. [文内引用:1]
14 Charman D J, Gehrels W R, Manning C, et al. 2010. Reconstruction of recent sea-level change using testate amoebae[J]. Quaternary Research, 73(2): 208-219. [文内引用:1]
15 Darienzo M E, Peterson C D, Clough C. 1994. Stratigraphic evidence for great subduction-zone earthquakes at four estuaries in Northern Oregon, USA[J]. Journal of Coastal Research, 10(4): 850-876. [文内引用:1]
16 Edwards R J, van de Plassche O, Gehrels W R, et al. 2004 a. Assessing sea-level data from Connecticut, USA, using a foraminiferal transfer function for tide level[J]. Marine Micropaleontology, 51(3): 239-255. [文内引用:2]
17 Frenzel P, Wrozyna C, Xie M, et al. 2010. Palaeo-water depth estimation for a 600-year record from Nam Co(Tibet)using an ostracod-based transfer function[J]. Quaternary International, 218(1-2): 157-165. [文内引用:1]
18 Fritz S C, Juggins S, Battarbee R W, et al. 1991. Reconstruction of past changes in salinity and climate using a diatom-based transfer function[J]. Nature, 352(6337): 706-708. [文内引用:1]
19 Geitzenauer K R, Roche M B, McIntyre A. 1976. Modern Pacific coccolith assemblages: Derivation and application to late Pleistocene paleotemperature analysis[J]. Geological Society of America Memoir, 145: 423-448. [文内引用:1]
20 Guibault J P, Clague J J, Lapointe M. 1995. Amount of subsidence during a late Holocene earthquake: Evidence from fossil tidal marsh foraminifera at Vancouver Island , west coast of Canada[J]. Palaeogeography, Palaeoclimatology, Palaeoecology, 118(1): 49-71. [文内引用:1]
21 Håkansson H. 1984. The recent diatom succession of Lake Havgårdssjön, south Sweden[A]. In: Mann D G(ed). Proceeding of the Seventh International Diatom Symposium[C]. Philadelphia: Otto Koeltz, 411-429. [文内引用:1]
22 Hamilton S L, Shennan Ⅰ. 2005 a. Late Holocene relative sea-level changes and the earthquake deformation cycle around the upper Cook Inlet, Alaska[J]. Quaternary Science Reviews, 24(12-13): 1479-1498. [文内引用:2]
23 Hassan G S, Espinosa M A, Isla F Ⅰ. 2009. Diatom based inference model for paleosalinity reconstructions in estuaries along the northeastern coast of Argentina[J]. Palaeogeography, Palaeoclimatology, Palaeoecolog, 275(1): 77-91. [文内引用:1]
24 Hawkes A D, Horton B P, Nelson A R, et al. 2011. Coastal subsidence in Oregon, USA, during the giant Cascadia earthquake of AD 1700[J]. Quaternary Science Reviews, 30(3-4): 364-376. [文内引用:1]
25 Hawkes A D, Horton B P, Nelson A R, et al. 2010. The application of intertidal foraminifera to reconstruct coastal subsidence during the giant Cascadia earthquake of AD 1700 in Oregon, USA[J]. Quaternary International, 221(1-2): 116-140. [文内引用:1]
26 Horton B P. 1999. The contemporary distribution of intertidal foraminifera of Cowpen Marsh, Tees Estuary, UK: Implications for studies of Holocene sea-level changes[J]. Palaeogeography, Palaeoclimatology, Palaeoecology, Special Issue, 149(1): 127-149. [文内引用:1]
27 Horton B P, Edwards R J. 2003. Seasonal distributions of foraminifera and their implications for sea-level studies[J]. SEPM(Society for Sedimentary Geology)Special Publication, (75): 21-30. [文内引用:2]
28 Horton B P, Corbett R, Culver S J, et al. 2006. Modern saltmarsh diatom distributions of the Outer Banks, North Carolina, and the development of a transfer function for high resolution reconstructions of sea level[J]. Estuarine Coastal and Shelf Science, 69(3-4): 381-394. [文内引用:1]
29 Imbrie J, Kipp N G. 1971. A new micropaleontological method for quantitative paleoclimatology;application to a late Pleistocene Caribbean core[A]. In: Turekian K K(ed). The Late Cenozoic Glacial Ages[C]. USA: Yale University Press, 71-181. [文内引用:1]
30 Juggins S. 2003. C2 User Guide: Software for Ecological and Palaeoecological Data Analysis and Visualisation[M]. UK: University of Newcastle, 7-70. [文内引用:2]
31 Leorri E, Horton B P, Cearreta A. 2008. Development of a foraminifera-based transfer function in the Basque marshes, N. Spain: Implications for sea-level studies in the Bay of Biscay[J]. Marine Geology, 251(1-2): 60-74. [文内引用:1]
32 Lepš J, Šmilauer P. 2003. Multivariate Analysis of Ecological Data Using CANOCO[M]. UK: Cambridge University Press, 1-282. [文内引用:1]
33 Minor R, Grant W C. 1996. Earthquake-induced subsidence and burial of late Holocene archaeology sites, Northern Oregon coast[J]. American Antiquity, 61(4): 772-781. [文内引用:1]
34 Nelson A R. 1992. Discordant14C ages from buried tidal-marsh soils in the Cascadia subduction zone, southern Oregon coast[J]. Quaternary Research, 38(1): 74-90. [文内引用:1]
35 Nelson A R, Asquith A C, Grant W C. 2004. Great earthquakes and tsunamis of the past 2000 years at the Salmon River estuary, central Oregon coast, USA[J]. Bulletin of Seismological Society of America, 94(4): 1276-1292. [文内引用:1]
36 Nelson A R, Sawai Y, Jennings A E, et al. 2008. Great-earthquake paleogeodesy and tsunamis of the past 2000 years at Alsea Bay, central Oregon coast, USA[J]. Quaternary Science Reviews, 27(7-8): 747-768. [文内引用:1]
37 Nelson A R, Ota Y, Umitsu M, et al. 1998. Seismic or hydrodynamic control of rapid late-Holocene sea-level rise in southern coastal Oregon, USA[J]. The Holocene, 8(3): 287-299. [文内引用:1]
38 Nelson A R, Shennan Ⅰ, Long A J. 1996. Identifying coseismic subsidence in tidal-wetland stratigraphic sequences at the Cascadia subduction zone of western North America[J]. Journal of Geophysical Research, 101(B3): 6115-6135. [文内引用:1]
39 Sachs H M. 1973. North Pacific radiolarian assemblages and their relationship to oceanographic parameters[J]. Quaternary Research, 3(1): 73-88. [文内引用:2]
40 Sawai Y, Horton B P, Nagumo T. 2004. The development of a diatom-based transfer function along the Pacific coast of eastern Hokkadio, northern Japan: An aid in paleoseismic studies of the Kurile subduction zone[J]. Quaternary Science Reviews, 23(23-24): 2467-2483. [文内引用:1]
41 Ter Braak C J F. 1986. Canonical correspondence analysis: A new eigenvector technique for multivariate gradient analysis[J]. Ecology, 67(5): 1167-1179. [文内引用:2]
42 Ter Braak C J F. 1987. The analysis of vegetation-environment relationships by canonical correspondence analysis[J]. Vegetatio, 69(1-3): 69-77. [文内引用:1]
43 Ter Braak C J F. 1996. Unimodal models to relate species to environment[A]. In: Centre for Biometry Wageningen. DLO-Agricultural Mathematics Group[C]. Netherland : Wageningen, 1-266. [文内引用:1]
44 Ter Braak C J F, Juggins S. 1993. Weighted averaging partial least squares regression(WA-PLS): An improved method for reconstructing environmental variables from species assemblages[J]. Hydrobiologia, 269-270(1): 485-502. [文内引用:11]
45 Ter Braak C J F, Šmilauer P. 2002. CANOCO Reference Manual and CanoDraw for Windows User's Guide: Software for Canonical Community Ordination(version 4. 5)[M]. USA: Microcomputer Power. [文内引用:2]
46 Zong Y, Horton B P. 1999. Diatom-based tidal-level transfer functions as an aid in reconstructing Quaternary history of sea-level movements in the UK[J]. Journal of Quaternary Science, 14(2): 153-167. [文内引用:1]
47 Zong Y, Kemp A C, Yu F, et al. 2010. Diatoms from the Pearl River estuary, China and their suitability as water salinity indicators for coastal environments[J]. Marine Micropaleontology, 75(1-4): 38-49. [文内引用:1]