李康, 李少华, 易雪斐, 徐亚楠, 王浩宇, 喻思羽. (2014)基于体素模型的砂岩侵入体三维重建[J]. 古地理学报, 16(6): 853-860
Li Kang, Li Shaohua, Yi Xuefei, Xu Ya'nan, Wang Haoyu, Yu Siyu. (2014)Sandstone injectite 3D reconstruction based on Voxelization[J]. Journal Of Palaeogeography, 16(6): 853-860. DOI:10.7605/gdlxb.2014.06.068  
Permissions
Copyright©2014, 《古地理学报》编辑部
版权所有.《古地理学报》编辑部
基于体素模型的砂岩侵入体三维重建
李康1, 李少华1, 易雪斐2, 徐亚楠3, 王浩宇1, 喻思羽1
1 长江大学油气资源与勘探技术教育部重点实验室,湖北武汉 430100
2 非常规油气湖北省协同创新中心,湖北武汉 430100
3 中国石油新疆油田分公司彩南油田作业区,新疆阜康 831511

通讯作者简介 李少华,男,1972年生,博士,教授,主要从事地质统计学及储层建模方面的科研与教学。E-mail: jpishli@163.com。

第一作者简介 李康,男,1990年生,长江大学地球科学学院硕士研究生,研究方向为储层地质建模。

收稿日期:2014-07-05
基金:国家“十二五”重大专项(编号:2011ZX05023-002)、国家自然科学基金项目(编号:42172136)联合资助
摘要

砂岩侵入体是由沉积后的砂岩再活动并侵入到周围地层中形成的一种特殊砂体。为了研究其演化过程,设计了砂岩侵入体形成过程的模拟实验。针对实验结果,提出了基于体素模型法和 Petrel软件的三维重建方法:在实验切片的基础上,对所得到的实验照片进行预处理,将其转化为 Petrel软件能够识别的 Gslib格式的数据体,再使用克里金插值算法进行模拟。结果表明,克里金算法可以很好地再现砂岩侵入体的外部形态,多组切片的特征参数统计可以定量地刻画出侵入体的形态,以期为实际岩性油气藏中的规模预测提供理论指导。

关键词: 砂岩侵入体; 体素模型法; 三维重建; 克里金插值
中图分类号:P512.2 文献标志码:A 文章编号:1671-1505(2014)06-0853-08
Sandstone injectite 3D reconstruction based on Voxelization
Li Kang1, Li Shaohua1, Yi Xuefei2, Xu Ya'nan3, Wang Haoyu1, Yu Siyu1
1 Key Laboratory of Exploration Technologies for Oil and Gas Resources, Ministry of Education, Yangtze University,Wuhan 430100,Hubei
2 Hubei Cooperative Innovation Center of Unconventional Oil and Gas,Wuhan 430100,Hubei
3 Cainan Oilfield Operation District,Xinjiang Oilfield Company,PetroChina,Fukang 831511,Xinjiang

About the corresponding author Li Shaohua,born in 1972,doctor,is a professor in Yangtze University. Now he is mainly engaged in geostatistics and reservoir modeling. E-mail: jpishli@163.com.

About the first author Li Kang,born in 1990,is a candidate for master degree in Yangtze University. Now he is engaged in reservoir geological modeling.

Abstract

Sand injectite is one kind of special sand bodies,which injects into surrounding strata after the depositional period. In order to analyze its evolution,a simulation experiment is designed. A 3D reconstruction method based on Voxelization is proposed,and Petrel software is used to simulate the results. Based on experiment slices, the slice photos are pre-processed,and then the data is changed into Gslib fromat. Kriging interpolation algorithm is carried out for the data. The simulation results show that Kriging interpolation algorithm can reconstruct the outlines of sand injectites well. Moreover,characteristic parameters of sand injectites are calculated to depict the shape quantitatively,so that it can provide theoretical models for prediction of lithological reservoir scale.

Key words: sand injectite; Voxelization; 3D reconstruction; Kriging interpolation algorithm

砂岩侵入体是由沉积后的砂岩再活动并侵入到周围地层中形成的一种特殊砂体。全球50多个深水盆地中都发现了从毫米级到千米级的砂岩侵入体, 如北海、挪威、地中海、丹麦、加利福利亚、英国大陆架、智利、几内亚海湾、澳大利亚海上和非洲西海岸海域等, 在中国南海北部珠江口盆地深水区域亦存在砂岩侵入或类似砂岩侵入的现象(张昌民等, 2012), 因此砂岩侵入体成为岩性油气藏勘探开发中值得注意的一个新领域。Chi等(2007)、张昌民等(2011)、易雪斐等(2012a)对砂岩侵入体形成机制进行了分析, 并归纳了砂岩侵入复合体的建筑结构要素及其特征(易雪斐等, 2012b)。国外学者在砂岩侵入体的测井地震响应(Huuse et al., 2007)、圈闭形成机理(Frey-Martinez et al., 2007)、识别标志(Briedis et al., 2007)等方面亦展开了广泛的研究。2011年, 英国利兹大学Ross教授对砂岩侵入体进行了实验室模拟。实验过程中, Ross等(2011)对有机玻璃管侧壁的现象进行了观察, 并对喷出过程作了相应的描述, 后来通常译作“ 砂火山” 现象。为了更好地说明地质条件下砂岩侵入和喷出的过程, 笔者对Ross等(2011)的实验进行了改进, 设计了砂岩侵入体模拟实验(易雪斐等, 2014)。在该实验的基础上, 为了更好地观察其内部结构, 并定量地描述砂火山的规模, 对实验成果体进行了切片(易雪斐等, 2014)。文中通过对切片图像的一系列处理, 结合体素模型法, 在Petrel软件中对实验体进行了三维重建, 最后通过模型综合分析, 定量地刻画出砂火山的形态以及规模。

1 模拟方法简介

三维重建是指通过对立体结构切片来获取二维信息, 然后对这些信息进行分析、模拟, 以恢复立体结构的三维信息(韩西安等, 2002)。三维重建技术被广泛应用于摄影学、建筑学、植物学、动物学、医学等领域:蔡钦涛(2004)通过对单幅图像处理, 对拍摄到的计算器图片进行了三维重建; 杨晔等(2011)设计对墙中线提取算法, 在AutoCAD软件中对室内建筑进行三维重建; 刘彦宏等(2002)利用基于图像的建模技术, 实现了一个从双视点图像重建树木三维模型的系统; 杨亮等(2009)基于多幅图像的黄瓜叶片建模方法, 更加快速、便捷、精确和逼真地重构出植物叶片的三维形态; 张玮和李杉(1999)探讨了通过多幅生物组织连续切片图像处理, 对可观察到的实体如脑、颅骨、神经、心脏进行重建的进展和方法。三维重建中经常用到基于图像的方法, 并进一步分为基于单幅图像和基于多幅连续切片图像的三维重建。对于本次重建而言, 基于单幅图像的三维重建方法只能还原拍摄到的现象、场景, 不能重现其内部结构, 更不能推测出未切片区的信息, 故采用基于多幅连续切片图像的三维重建。

体素模型法(王旭等, 2000; 侯增选等, 2005)是以单个小立方体为基本单位, 通过还原每一个单位立方体的属性, 进而还原整个立方体属性的重建方法, 即以体素作为三维图像基本单元的一种重建方法。基于体素模型的三维重建过程即运用体素模型的方法, 将生成的属性体导入到Petrel软件中, 再使用克里金插值算法进行模拟的过程。

2 砂岩侵入体的三维重建
2.1 实验切片图像的网格化

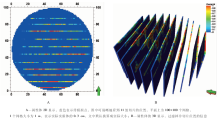
本次实验的模型设计、实验流程及对实验结果进行的冷冻切片见易雪斐等(2014)。实验过程中采用了2种砂体, 分别是粉砂(200目的玻璃微珠与红色示踪剂混合, 显示为红色)和细砂(80目的玻璃微珠), 共进行了5组实验。实验开始时, 顶部为3 cm厚的细砂(白色)、中部为1 cm厚的粉砂(红色)、底部为8 cm厚的细砂(白色)。实验结束后, 对本次实验结果进行冷冻切片。实验体(图 1, 30 cm× 30 cm× 12 cm)正下方为坐标原点, 水平方向为X轴, 平面上垂直于X方向为Y轴, 沿着平行于X轴的方向进行一系列垂直切片(Y=a cm 切片指距离原点O为a cm)。本次模拟实验切片时基本上保持2 cm的间距, 共取得11组切片, 分别是Y=1.5 cm、Y=3.5 cm、Y=6 cm、Y=8 cm、Y=10.5 cm、Y=13.5 cm、Y=16 cm、Y=18.5 cm、Y=21.5 cm、Y=24 cm和Y=26 cm的切片(易雪斐等, 2014)。这些切片不仅有利于观察实验体内部的沉积构造, 也为三维重建奠定了基础。图1为其中一次实验的顶面、侧面及切片结果。

图1 砂岩侵入体模拟中的一次实验结果(据易雪斐等, 2014, 有修改)Fig.1 A result of sandstone injectite simulation (modified from Yi et al., 2014)

假设实验切片图像由红色和白色的像素点组成。将切片图像划分成若干个网格, 每一个网格又包含若干个像素点, 并将其中红色像素点所占的比例定义为这个网格的属性值。由于实验切片只能得到部分实验模型的信息, 故需要应用插值的方法进行三维重建。在实际实验体中一个网格体内属性值非均质性较弱的情况下, 采用几何平均的方法, 能够客观地恢复实验模型的真实特征。

具体的网格化过程就是将研究对象(实验体)划分成若干个体素, 空间位置以x、y、z表示, 在x轴上划分为100个单元, 在y 轴上划分为100个单元, 在z轴上划分为40个单元。研究对象可用100× 100× 40个体素来表示, 这些体素按照自身的空间位置组合即构成研究对象的三维形态。空间上每一个体素均具有某一类属性值(每个网格红色像素的比例, 红色为1, 白色为0, 待估点为-99.99), 并以数值型数据来表征。这种三维数据的基本格式如下:(x1, y1, z1, attribute1), (x2, y2, z2, attribute2), (x3, y3, z3, attribute3)……其中attribute表示属性, 代表了显示的内容。但由于这些体素是均匀的分布在三维空间, 即x、y、z方向上, 网格点之间的距离均相等, 所以无需给出各个数据点的空间坐标, 只要给出三维网格某一个角点的空间位置和某一数据点的序号, 即可以根据网格间距所对应的距离求出该点的空间位置。在应用中, 只需要把属性值按x、y、z轴的顺序写入数据文件, 而省略各个体素的x、y、z值(据胡水清等, 2005, 有修改)。

2.2 利用Petrel软件建立三维模型

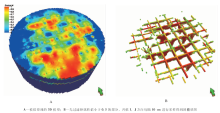
由于是在实验室内进行的实验模拟, 因此没有建立三维构造模型, 而是直接在Petrel软件里建立1个simple gid网格属性体, 即对实验体按100× 100× 40个网格进行细分, 然后加载Gslib属性体的数据文件。如图2-B为Petrel软件显示的待模拟三维切片属性体。

图2 属性体2D和3D窗口显示Fig.2 2D and 3D window display of attribute volume

通常情况下, 对某地区储集层进行三维建模研究必须获取本地区的井位以及测井数据, 在无井条件下通常需设置虚拟井(蔡冬梅等, 2008; 王萍等, 2009; 黄安敏等, 2011)。设置虚拟井亦是文中模型建立的关键步骤之一, 具体过程为:在属性体2D窗口(图 2-A)下, 假设切片上每个网格为1口井, 井在网格的正中心, 例如, 左上的第1个网格wellname设置成A1, x坐标23.5, y坐标86.5, kb为0, md为40; 依次类推设置虚拟井, 据统计共设置虚拟井854口, 这样设置的好处是使得正东方向的平均井距为1 m; 设置完成后, 反提取属性数据, 即将属性体上的值通过Make logs 方式赋值到每口井上, 最后用Arithmetic方法对测井数据进行粗化。

克里金插值是以估值结果的无偏性和最优性为限制条件, 求解已知数据在估算未知点数据时最适当的权重, 加权求和得到估值结果, 同时得到克里金误差方差, 用以表示估值的不确定性(李少华等, 2012)。利用变差函数分析(图 3), 结合克里金算法, 对切片模型进行三维模拟。根据常规变差函数设置参数的方法(周游等, 2010; 王家华和刘倩, 2011), 确定正东方向的虚拟井距都是0.3 cm, 主方向为270° , 垂直方向为180° , 步长为0.3 cm, 带宽为步长的2倍, 厚度为单层最小厚度(0.3 cm), 角度容限为45° , 步长容限为50%。由于实验体的顶面是圆形的砂火山口, 故将搜索半径和主次变程设置为相同, 以让搜索范围尽量成圆形, 其中搜索半径不大于最大虚拟井距的一半, 为18 cm。块金值在地质统计学上称为“ 块金效应” , 表现为在很短的距离内有较大的空间变异性, 在实际建模过程中, 考虑到模拟结果的连续性, 通常将块金值设为0(图 3为了美观块金值不为0, 实际块金值为0)。通过多次改变主变程和次变程大小, 发现主、次变程均在18 cm以下时, 模拟体的表面都有像条带一样的形态, 且砂火山的形态受到切片位置的限制, 故将主变程和次变程都设置为18 cm, 垂直变程设置为3 cm。

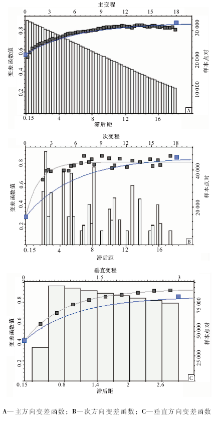图3 主方向、次方向和垂直方向的变差函数Fig.3 Variational function in principal direction, secondary direction and vertical direction

将利用克里金插值法算出的结果(图 4)与实验体顶面(图 1-A)相比发现, 利用该方法模拟得到的砂火山形态比较理想, 表明克里金插值方法在图像修复方面效果良好。这主要是由于克里金插值法是运用空间结构分析进行估值, 充分利用了数据空间场的性质, 故可以很好地反映空间场的各向异性; 同时亦较好地利用了未采样处的空间相关性, 且可以通过采样点空间分布的自动识别来改变权值的大小, 从而消除了因为采样不均(设置的虚拟井同一行Y值相同)而形成的误差(蔡占川等, 2013)。

图4 利用克里金插值得到的模型结果栅状图Fig.4 Model result and fence diagram using Kriging interpolation

3 模拟结果分析

图5-A中, 自上而下依次为Y=13.2 m(实验切片)、Y=15 cm(模拟)及任意与水平方向斜交的方向上(模拟)的3个切片的剖面图显示结果, 这些结果均很好地刻画了砂火山的形态和大小, 也再次证明了克里金插值法在图像修复方面效果良好。图5-B为Y=15 cm和任意方向的切片叠置后的三维显示效果, 从该结果的显示来看, 根据Petrel三维重建以后得到的模型比实际实验结果更具有优势, 即模型切片可以显示任意方向的几条叠置的切片、更有立体感, 而实验体只能观察到顶面和侧面的现象, 并只能定性地描述砂火山; 另外, 可以通过统计模型中每个切片上的砂火山所占的网格数来定量地刻画砂火山的规模, 这有助于对砂火山的体积进行计算。

图5 模型切片的显示Fig.5 Showing of model slices

通过实验只得到了11组沿着Y轴方向的切片图片(图1-C), 而通过模型则可以得到沿X, Y, Z轴方向的多组切片。为更加直观地观察其内部结构, 沿Z轴方向进行切片(图6), 如Z=3.3 cm, Z=2.7 cm, Z=2.1 cm, Z=1.5 cm, Z=0.9 cm, Z=0.3 cm。通过沿Z轴方向的切片(图6), 可以明显看出“ 砂火山” 管道形成演化的过程, 即水平方向上, 红色物质所占的面积越来越大, 这也和垂直剖面上的“ V” 形侵入有很好的对应关系。

图6 Z方向模型切片的2D显示Fig.6 2D showing of model slices in Z axle direction

通过沿着Y轴的模型切片可以观察到, 砂火山最大垂向厚度为3.9 cm, 平均厚度为2.4 cm。通过沿着Z轴方向的模型切片可以观察到砂火山最大半径为4.5 cm, 平均半径为3 cm。根据上述结论认为, 砂火山是底部平均半径为3 cm、平均高度为2.4 cm的圆锥体。统计每一块模型切片上砂火山的个数和面积, 再将其从理论上换算成实际地层1 km2中的面积, 就可以得出理论上实际岩性油气藏地层中砂火山的面积, 同时也可以对砂火山体积进行换算。

4 结论

1)利用体素法原理, 结合多种绘图软件对得到的模拟实验照片进行预处理, 得到了能够和Petrel软件对接的Gslib数据体。

2)采用设置虚拟井的方法反提取虚拟井上的属性值, 然后对其粗化, 再使用克里金插值算法对实验切片属性体进行模拟, 并多次改变变差函数参数, 使得模拟的顶面和实际顶面吻合。三维重建结果表明克里金插值法在图像修复方面效果良好。

3)对从实验得到的切片照片进行处理后建立模型, 根据模型得到的X, Y, Z多组切片定量地刻画出砂火山的形态, 这很好地解决了实验过程不能定量刻画砂火山形态的问题。

参考文献
1 蔡冬梅, 陈烨菲, 赵伦, 等. 2008. 随机建模技术在国外某大型碳酸盐岩油田的应用[J]. 大庆石油地质与开发, 27(8): 27-30. [文内引用:1]
2 蔡钦涛. 2004. 基于图像的三维重建技术研究[D]. 浙江杭州: 浙江大学硕士论文. [文内引用:1]
3 蔡占川, 姚菲菲, 唐泽圣. 2013. 基于克里金插值法的图像修复[J]. 计算机辅助设计与图形学学报, 25(9): 1281-1286. [文内引用:1]
4 黄安敏, 李林, 王立华, 等. 2011. 虚拟井技术在深水无井区碎屑岩储集层预测中的应用[J]. 石油物探, 50(3): 282-287. [文内引用:1]
5 韩西安, 杨海涛, 邱明明, 等. 2002. 基于切片图像的血管三维重建方法[J]. 装备指挥技术学院学报, 13(3): 85-91. [文内引用:1]
6 胡水清, 侯慧群, 韩邵阳. 2005. 基于体素模型的三维显示技术[J]. 物探与化探, 29(3): 265-268. [文内引用:1]
7 侯增选, 张定华, 杨海成. 2005. 体素模型表面优化提取方法及图形显示[J]. 机械科学与技术, 4(3): 361-367. [文内引用:1]
8 李少华, 张昌民, 尹艳树. 2012. 储集层建模算法剖析[M]. 北京: 石油工业出版社, 36-54. [文内引用:1]
9 刘彦宏, 王洪斌, 杜威. 2002. 基于图像的树类物体的三维重建[J]. 计算机学报, 25(9): 1-5. [文内引用:1]
10 王家华, 刘倩. 2011. 储集层建模中对变差函数分析的几点认识[J]. 石油化工应用, 30(10): 5-7. [文内引用:1]
11 王萍, 唐潋, 马楠, 等. 2009. 一种基于虚拟井和多层对比的地层对比方法[J]. 天津大学学报, 42(8): 741-750. [文内引用:1]
12 王旭, 卿侯, 林天义. 2000. 基于体素模型的体绘制算法[J]. 西北工业大学学报, 18(1): 78-81. [文内引用:1]
13 吴胜和, 张一伟, 李恕军, 等. 2001. 提高储集层随机建模精度的地质约束原则[J]. 石油大学学报, 25(1): 55-58. [文内引用:1]
14 杨亮, 郭新宇, 陆声链. 2009. 基于多幅图像的黄瓜叶片形态三维重建[J]. 农业工程学报, 25(2): 14-143. [文内引用:1]
15 杨晔, 姜晓彤, 况迎辉, 等. 2011. 基于图形理解的室内建筑三维重建算法[J]. 信息与电子工程, 9(1): 105-108. [文内引用:1]
16 易雪斐, 张昌民, 李少华, 等. 2012 a. 砂岩侵入体的形成机制分析[J]. 古地理学报, 14(6): 727-731. [文内引用:1]
17 易雪斐, 张昌民, 李少华, 等. 2012 b. 砂岩侵入复合体的建筑结构要素及其特征[J]. 地质论评, 58(2): 329-325. [文内引用:1]
18 易雪斐, 张昌民, 李少华, 等. 2014. 砂岩侵入体系物理模拟实验[J]. 古地理学报, 16(5): 605-612. [文内引用:3]
19 张昌民, 张尚峰, 朱锐, 等. 2011. 砂岩侵入体: 岩性油气藏勘探开发中值得注意的一个新领域[J]. 岩性油气藏, 23(2): 1-8. [文内引用:1]
20 张昌民, 张尚锋, 朱锐, 等. 2012. 珠江口盆地砂岩侵入体的识别特征及其石油地质意义[J]. 石油学报, 33(2): 188-194. [文内引用:1]
21 张玮, 李杉. 1999. 生物组织连续切片图像的计算机三维重建研究的进展[J]. 生物医学工程学杂志, 16(3): 377-381. [文内引用:1]
22 周游, 程时清, 张敏. 2010. 储集层建模中变差函数参数的设置[J]. 西安石油大学学报(自然科学版), 25(5): 25-28. [文内引用:1]
23 Briedis N A, Bergslien D, Hjellbakk A, et al. 2007. Recognition criteria, significance to field performance, and reservoir modeling of sand injections in the Balder field, North Sea[A]. In: Hurst A, Cartwright J(eds). Sand Injectites: Implications for Hydrocarbon Exploration and Production[C]. AAPG Memoir, 87: 91-102. [文内引用:1]
24 Chi Guoxiang, Xue Chunji, Lai Jianqing, et al. 2007. Sand injection and liquefaction structures in the Jinding Zn-Pb deposit, Yunnan, China: Indicators of an over pressured fluid system and implications for mineralization[J]. Economic Geology, 102(4): 739-743. [文内引用:1]
25 Frey-Martinez J, Cartwright J, Hall B, et al. 2007. Clastic intrusion at the base of deep-water sand s: A trap-forming mechanism in the eastern Mediterranean[A]. In: Hurst A, Cartwright J(eds). Sand Injectites: Implications for Hydrocarbon Exploration and Production[C]. AAPG Memoir, 87: 49-63. [文内引用:1]
26 Huuse M, Cartwright J, Hurst A, et al. 2007. Seismic characterization of large-scale sand stone intrusions[A]. In: Hurst A, Cartwright J(eds). Sand Injectites: Implications for Hydrocarbon Exploration and Production[C]. AAPG Memoir, 87: 21-35. [文内引用:1]
27 Ross J A, Peakall J, Keevil G M. 2011. An integrated model of extrusive sand injectites in cohesionless sediments[J]. Sedimentology, 58(7): 1693-1715. [文内引用:1]
28 Jonk R, Hurst A, Duranti D, et al. 2005. Origin and timing of sand injection, petroleum migration, and diagenesis in Tertiary reservoirs, south Viking Graben, North Sea[J]. AAPG Bulletin, 89(3): 329-357. [文内引用:1]
29 Shanmugam G, Shrivastava S K, Das B. 2009. Sand y debrites and tidalites of Pliocene reservoir sand s in upper-slope canyon environments, offshore Krishna-Godavari Basin(India): Implications[J]. Journal of Sedimentary Research, 79(9): 736-756. [文内引用:1]