金振奎, 石良, 闫伟, 朱小二, 彭飚. (2016)沉积和成岩因素对碎屑岩储集层质量贡献率的定量分析方法——单因素比较法* [J]. 古地理学报, 18(4): 535-544
Jin Zhenkui, Shi Liang, Yan Wei, Zhu Xiao er, Peng Biao. (2016)Contribution of sedimentary and diagenetic factors to clastic reservoir quality: Quantitative determination by single factor comparison method[J]. Journal Of Palaeogeography, 18(4): 535-544. DOI:10.7605/gdlxb.2016.04.039  
Permissions
Copyright©2016, 《古地理学报》编辑部
版权所有.《古地理学报》编辑部
沉积和成岩因素对碎屑岩储集层质量贡献率的定量分析方法——单因素比较法*
金振奎1, 石良2, 闫伟1, 朱小二1, 彭飚1
1 中国石油大学(北京)地球科学学院,北京 102249
2 中国石油冀东油田勘探开发研究院,河北唐山 063004

第一作者简介 金振奎,男,1963年生,教授,博士生导师,从事沉积学和储集层成岩作用方面的研究。E-mail: jinzhenkui@188.com。

通讯作者简介 石良,男,1985年生,博士,主要从事沉积岩石学与储集层地质学研究工作。E-mail: sh1558661@163.com。

收稿日期:2016-03-29
基金:*国家重大科技专项“油气勘探领域储集层地质与油气评价”(编号:2009ZX05009-002)项目资助; [Financially suppored by National Science and Technology Major Projects of “Reservoir geology and oil and gas evaluation in the field of oil and gas exploration”(No.2009ZX05009-002)]
摘要

碎屑岩储集层质量在此指其渗透率和孔隙度。影响储集层质量的因素主要是沉积方面和成岩方面。沉积方面的因素包括粒度、磨圆度、分选系数和杂基含量等,成岩方面的因素包括压实强度、溶蚀孔隙含量、胶结物类型和含量等。一种砂岩储集层的质量往往是多种单因素共同作用的结果,如何理清每个因素的具体贡献率是确定主控因素的关键。作者提出了一种分析各种沉积和成岩因素对储集层质量定量贡献率的方法——单因素比较法,并以渤中凹陷古近系东营组砂岩为例进行了演示分析。该地区东营组三角洲平原分流河道砂岩与三角洲前缘河口坝砂岩储集物性差异巨大,计算了各个因素对这种差异的贡献率,确定了主控因素:杂基含量差异的贡献率为78.5%,是主控因素;粒度差异的贡献率为2.7%,分选系数差异的贡献率为1.5%,自生黏土矿物含量差异的贡献率为15.9%,碳酸盐胶结物含量差异的贡献率为2.3%,溶孔含量差异的贡献率为1.5%,压实强度差异的贡献率为1.7%。沉积因素的综合贡献率为各沉积单因素的贡献率之和,为82.7%;成岩因素的综合贡献率为各成岩单因素的贡献率之和,为18.4%(其中溶孔的影响与其他因素相反,即为-1.5%)。因此,沉积因素是导致该储集层质量差异的主要因素。

关键词: 储集层质量; 主控因素; 单因素比较法; 古近系; 东营组; 渤中凹陷
中图分类号:TE122.2+4 文献标志码:A 文章编号:1671-1505(2016)04-0535-10
Contribution of sedimentary and diagenetic factors to clastic reservoir quality: Quantitative determination by single factor comparison method
Jin Zhenkui1, Shi Liang2, Yan Wei1, Zhu Xiao er1, Peng Biao1
1 College of Geosciences,China University of Petroleum(Beijing),Beijing 102249,China
2 Research Institute of Exploration and Development,Jidong Oilfield Company,PetroChina, Tangshan 063004,Hebei

About the first author Jin Zhenkui,born in 1963,is a professor and Ph.D. supervisor. He is mainly engaged in sedimentology and reservoir diagenesis. E-mail: jinzhenkui@188.com.

About the corresponding author Shi Liang,born in 1985,is a Ph.D. He is mainly engaged in sedimentology petrology and reservoir geology. E-mail: sh1558661@163.com.

Abstract

Quality of clastic reservoirs refers to permeability and porosity. Factors controlling reservoir quality are mainly sedimentary and diagenetic. Sedimentary factors include grain size,rounding,sorting and content of clay matrix. Diagenetic factors include compaction degree,content of dissolution pores,type and content of cements. The reservoir quality of a sandstone is commonly controlled by many factors,and the key to determine major controlling factors is to find out quantitative contribution of each factor. In this paper,a method to analyze quantitative contribution of sedimentary and diagenetic factors to reservoir quality—the single factor comparison method—is proposed out,and is applied to the sandstone reservoirs in the Dongying Formation of Paleogene in the Bozhong sag. There are two types of sandstones in the Dongying Formation,distributary channel sandstone and mouth bar sandstone of deltaic facies,and their permeability differs greatly. Quantitative contribution rate of each factor to the reservoir quality difference is calculated,and major controlling factor is determined:Contribution rate of clay matrix content is 78.5%,indicating clay matrix content is the major controlling factor;that of grain size is 2.7%,that of sorting coefficient is 1.5%;that of authigenic clay mineral content is 15.9%,that of carbonate cement content is 2.3%,that of dissolution pore content is 1.5%,that of compaction degree is 1.7%. Comprehensive contribution rate of sedimentary factors is the sum of each sedimentary factor's contribution rate, i.e., 82.7%;comprehensive contribution rate of diagenetic factors is the sum of each diagenetic factor's contribution rate, i.e., 18.4%(the rate of dissolution pore is -1.5% because of its reverse influence). Thus,sedimentary factors are major factors resulting in great difference in permeability between channel sandstone and mouth bar sandstone in this area.

Key words: reservoir quality; controlling factors; single factor comparison method; Paleogene; Dongying Formation; Bozhong sag

关于碎屑岩储集层质量(指孔隙度和渗透率)的影响因素, 前人做了很多研究(Ehrenberg, 1990; Salem et al., 2000; Rossi et al., 2001; Salem, 2005; 王京等, 2006; 金振奎和刘春慧, 2008; 王瑞飞和孙卫, 2009; 谢润成等, 2010; 郑占等, 2010; 金振奎等, 2011; 胡作维等, 2012; 付晶等, 2013; 董月霞等, 2014)。这些因素主要是两大类, 即沉积方面和成岩方面。有些情况下, 构造方面的因素(裂缝)也有一定影响。沉积方面的影响因素包括粒度、分选系数、填隙物类型和含量等。成岩方面的影响因素包括压实、胶结和溶蚀。可见, 储集层质量影响因素往往有多种。预测地下储集层的质量和分布, 需要找出其质量主控因素。要做到这一点, 就需要确定各个因素具体的影响程度, 即定量的贡献率。例如, 某砂岩储集层孔隙度和渗透率很低, 质量很差, 这有可能主要是沉积因素导致的, 也有可能主要是成岩因素导致的。怎样定量地确定沉积因素和成岩因素各自的贡献率?譬如说分别是90%和10%?还是20%和80%?沉积因素又包括粒度、分选性、填隙物等, 怎样确定各个沉积因素具体的贡献率?成岩因素又包括压实、胶结、溶蚀等, 怎样确定每种成岩作用具体的贡献率?以往没有针对各影响因素进行定量分析, 常常难以明确地确定主控因素。

作者提出了一种分析各种沉积和成岩因素对储集层质量定量贡献率的方法, 并以渤中凹陷古近系东营组碎屑岩储集层为例进行了演示。这种方法为确定储集层质量主控因素开辟了一条新的途径。

1 基本原理

影响碎屑岩储集层质量最重要的参数是储集层的渗透率, 因为不论是在标准SY/T 6285-2011, 还是低渗储集层评价建议标准(杨玉卿等, 2010), 渗透率都是划分各类储集层最重要的参数, 也就是说, 碎屑岩储集层的分类方案主要是按照渗透率的大小来划分的。因此, 通过分析各因素对渗透率的影响, 就可以确定其对储集层质量的影响。这是本文的立脚点。

1.1 相关概念和计算公式

渗透率可以直接测定, 也可通过理论计算得到, 公式如下(Carman, 1937; Loudon, 1952):

式中, k为渗透率, m2; KC-K为Kozeny-Carman常数, 常取5(Carman, 1937), 无量纲; φ 为孔隙度, %; S为比表面, m-1。

式(1)是本文定量分析的理论基础。从式(1)中可知, 岩石渗透率(k)的大小只与多孔介质的2个固有参数有关, 即比表面(S)和孔隙度(φ )。需指出, 式(1)适用于孔隙度小于70%的多孔介质, 且流体的雷诺数较低(小于1~10)(严宗毅, 2002), 不适用于裂缝发育的岩石(Childs and Collis-George, 1950)。

比表面(S)指单位体积多孔介质的总表面积, 其计算公式如下(Blake, 1922):

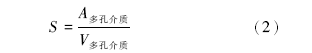
式中, S为多孔介质的比表面, m-1; A多孔介质为多孔介质的总表面积(颗粒表面积+填隙物表面积), m2; V多孔介质为多孔介质的总体积, m3。

多孔介质的比表面(S)由2部分组成:颗粒比表面(S颗粒)和填隙物比表面(S填隙物)(Loudan, 1952; Petersen et al., 1996; Jong, 1999; Yukselen and Kaya, 2006)。

颗粒比表面(S颗粒)用以下公式进行计算(Fair et al., 1933; Loudan, 1952; Carrier, 2003):

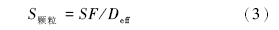
式中, Deff为颗粒等效粒径, m; SF为颗粒形状系数, 无量纲。对于砂岩, Fair等(1933)给出了SF取值, 颗粒为圆球状取6.0, 圆状取6.1, 次圆取6.4, 次棱状取7.4, 棱角状取7.7。由公式(3)可知, 颗粒的比表面仅与颗粒的等效粒径有关。

颗粒的等效粒径(Deff)用粒度分析资料进行计算, 公式如下(Carrier, 2003):

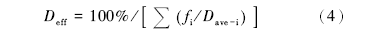
式中, fi为某粒径区间颗粒的百分含量, %; Dave-i为某粒径区间的平均粒径, m。

Dave-i的计算方法如下(Carrier, 2003):

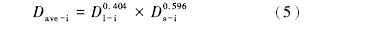
式中, Dl-i为粒度分析某粒径区间中的最大粒径数值, m; Ds-i为粒度分析某粒径区间中的最小粒径数值, m。

填隙物的比表面与其矿物类型和含量有关。

如果填隙物是黏土矿物, 其比表面(S黏土)既可以直接测量, 也可以据其含量(f黏土)和该黏土矿物的比表面积()( 表 1)进行计算得到, 其公式如下(Churchman and Burke, 1991):

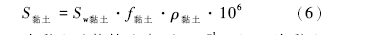
式中, S黏土为黏土矿物的比表面, m-1; Sw黏土为黏土矿物的比表面积, m2/g; f黏土为黏土矿物的含量, %; ρ 黏土为黏土矿物的密度, g/cm3。比表面积(Sw)是指单位质量固态物质的表面积, 单位为m2/g, 与比表面概念相近但不同, 通常用N2吸附BET法测定(Metz et al., 2005)。前人已经测定了各类黏土矿物的和ρ 黏土( 表 1), 可直接应用, 因此只要知道了黏土矿物的含量, 就可以确定其比表面。

表1 黏土矿物N2吸附(BET法)的比表面积(Sw) Table1 Specific surface area(Sw) of clay minerals by BET method

填隙物如果是非黏土矿物胶结物, 如碳酸盐胶结物、硅质胶结物和黄铁矿等, 则其比表面很小, 可以忽略, 因为在这些胶结物的晶粒之间基本不存在可使水或油气充注的有效孔隙, 且晶面光洁(Churchman and Burke, 1991)。但这些胶结物会占据孔隙空间, 影响孔隙度, 因而会影响渗透率。

因此, 砂岩的总比表面(S)计算公式如下:

式中, φ 为孔隙度, %; φ 填隙物为砂岩中填隙物的含量, %。

由上述各公式可见, 对于常规碎屑岩储集层, 只要知道了岩石的孔隙度、粒度、磨圆度、黏土杂基的含量、黏土胶结物的类型和含量、非黏土矿物胶结物的类型和含量, 就可以计算理论渗透率。

通过岩心实测, 可以得到孔隙度和渗透率。通过粒度分析得到粒度。通过薄片观察, 可以确定颗粒的磨圆度、填隙物的类型和含量, 可确定自生黏土矿物含量和黏土杂基含量。通过扫描电镜观察, 可以确定自生黏土矿物的类型。通过X射线衍射分析, 可以确定岩石中黏土矿物的类型和含量。可见, 黏土矿物的类型和含量可通过多种手段获得, 可以相互校正。

1.2 定量分析方法— — 单因素比较法

影响储集层渗透率的每一个因素在此称“ 单因素” 。

沉积方面的单因素, 简称沉积单因素, 主要包括等效粒径(颗粒大小及磨圆度)、分选系数和黏土杂基含量。

成岩方面的单因素, 简称成岩单因素, 主要是胶结、压实和溶蚀这3种成岩作用。

胶结作用通过影响胶结物的类型和含量来影响孔隙度和比表面, 进而影响渗透率。压实作用通过降低孔隙度来影响储集层渗透率。溶蚀作用通过增加孔隙度来影响储集层渗透率。

每个单因素对渗透率的影响程度用“ 贡献率” 表示。怎样确定每个单因素对渗透率具体的贡献率呢?作者提出了“ 单因素比较法” 。其基本原理是:假定只有一个单因素数值发生变化, 而其他单因素不变时, 计算渗透率的变化; 然后, 通过比较每个单因素引起的渗透率变化大小, 决定哪个单因素对渗透率的影响是主要的。

主控因素分析可针对2种情况:第1种是单一砂岩渗透率的主控因素分析; 第2种是导致2种砂岩渗透率差异的主控因素分析。

1.2.1 单一砂岩渗透率主控因素分析方法 单一砂岩渗透率主控因素分析是指确定某一砂岩渗透率的主控因素。作者提出通过比较砂岩的初始渗透率与单因素变化后的渗透率, 来确定主控因素。具体步骤如下:

1)单因素数值准确性检验。根据砂岩实验分析得到的孔隙度、粒度、磨圆度、黏土杂基的含量、黏土胶结物的类型和含量、非黏土矿物胶结物的类型和含量、次生孔隙体积率等单因素的数值, 计算其理论渗透率。如果理论渗透率与实测渗透率相近, 则说明获得的各单因素数值是准确的, 可以进行下一步计算; 否则就要重新检查。

2)计算出砂岩的“ 初始渗透率” (用k0表示)。初始渗透率和初始孔隙度是指砂岩在埋藏前(即刚沉积不久)且不含任何填隙物时的渗透率和孔隙度, 此时没有发生任何成岩作用。砂岩的这种状态可称“ 初始状态” 。初始渗透率只与粒径、磨圆度和分选系数有关, 根据公式(1)求取。公式(1)中的φ 为初始孔隙度(φ 0)。初始孔隙度只与分选系数有关, 计算公式如下(Scherer, 1987):

式中, S0为Trask分选系数, 无量纲; φ 0为初始孔隙度, %。

3)计算某一单因素发生变化后的渗透率。通过薄片(铸体薄片或普通薄片)观察、扫描电镜观察、X衍射分析和粒度分析, 确定可能影响该砂岩渗透率的各种单因素。然后, 根据公式(7)和公式(1), 计算出某一单因素发生变化后的渗透率, 假定其他单因素保持不变, 均为初始状态的单因素数值。某一单因素发生变化后的渗透率用k单表示。

4)计算单一因素对渗透率的贡献率, 用I单表示, 其计算公式如下:

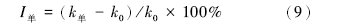
杂基含量的增加、胶结物含量的增加、压实强度的增加都会降低渗透率, I单是负值; 溶蚀孔隙的增加会提高渗透率, I单是正值。比较贡献大小时, 需用绝对值, I单的绝对值越大, 代表该单因素对渗透率影响越大。通过比较各单因素贡献率的绝对值, 就可以确定主控因素。

1.2.2 2种砂岩渗透率差异主控因素分析方法 2种砂岩渗透率差异主控因素分析, 是指当对比的2种砂岩渗透率有差异时, 找出导致这种差异的主要因素。具体分析方法与单一砂岩渗透率主控因素分析法相似, 都需要比较, 所不同的主要是:对单一砂岩, 是将其现在的渗透率和相关参数与初始状态的比较; 对于2种砂岩, 是直接比较其现在的渗透率和相关参数。具体步骤如下:

1)单因素数值准确性检验。根据砂岩A和砂岩B实测得到的有关单因素数值, 计算出其理论渗透率, kA和kB。如果理论渗透率与实测渗透率相近, 则说明获得的各参数是准确的, 可以进行下一步计算; 否则就要重新检查。

2)根据砂岩A和砂岩B的理论渗透率, 求出其的理论渗透率比值R或差值Δ k。R=kA/kB; Δ k=kA-kB, Δ k用绝对值表示, 不分正负。

3)分析每个单因素差异引起的渗透率差异。通过薄片观察和扫描电镜观察, 确定可能影响砂岩A和砂岩B渗透率的各种单因素, 并确定两者哪些单因素有差异。然后, 在假定只有1个单因素不同(譬如杂基含量不同), 而其他单因素相同(其数值可统一采用砂岩A或B的)的情况下, 根据公式(1), 计算出砂岩A和砂岩B各自的理论渗透率, kA单和kB单, 求出kA单和kB单的比值R单或者差值Δ k单。R单=kA单/kB单; Δ k单=kA单-kB单。Δ k单用绝对值表示, 不分正负。

对于沉积单因素(等效粒径、分选系数、黏土杂基含量), 都有具体的实验数值, 可直接代入公式(7)和(1)进行计算。

对于成岩单因素, 则需通过计算后得到相关数值。压实作用的强弱用“ 压实减孔量” 表达, 胶结作用的强弱用胶结物的含量表达, 溶蚀作用的强弱用“ 溶蚀孔隙度” 表达, 计算公式参见石良等(2015a, 2015b)。

4)计算单一因素对砂岩A和砂岩B理论渗透率差异的贡献率I单。I单可用2种方法计算。一种是用差值计算, I单=Δ kd单/Δ kd× 100%。这样计算出来的I单是有正负的。不过比较贡献率大小时, I单均用绝对值表示。I单越大, 说明该单因素的贡献率越大。

另一种是用比值计算, I单=R单/R× 100%。这种计算方法的优点是简便, 因为计算比值比计算具体渗透率数值容易, 公式中有些相同的项可直接约掉。但用此方法时需注意, R和R单必须都大于1或都小于1。如果R大于1, 而个别单因素的R单小于1, 则需用R单的倒数与R相比。例如, 如果R为10, R单为0.5, 那么I单=1/R单÷ R× 100%=2÷ 10× 100%=20%。

分析贡献率大小时, 2种计算方法没有差别, 只要对各单因素都用同一计算方法就行。比较贡献率大小时, I单均用绝对值表示, 不分正负。I单越大, 说明该单因素的贡献率越大。

1.2.3 沉积和成岩综合贡献率计算方法 “ 综合贡献率” 就是相关单因素的贡献率之和。沉积综合贡献率是等效粒径、分选系数、黏土杂基含量这3个单因素的贡献率之和。成岩综合贡献率是压实、胶结和溶蚀这3种成岩作用的贡献率之和。通过比较综合贡献率的大小, 就可以确定储集层质量控制因素究竟是以沉积为主还是以成岩为主, 或者两者都重要。

计算综合贡献率时, 各单因素的贡献率是有正、负之分的, 不用绝对值, 因为有的单因素会降低渗透率, 而有的会提高渗透率。在此可以规定, 降低渗透率的贡献率为正值, 提高的则为负值。

2 应用实例

现以渤中凹陷古近系东营组砂岩储集层为例, 分析其质量主控因素。

渤中凹陷是渤海湾盆地的二级构造单元, 是重要的生油气中心, 总面积约8660, km2(傅强等, 2010)。渤中凹陷古近系沉积厚度为2000~5000, m, 自下而上发育孔店组、沙河街组和东营组, 由灰色砂岩、粉砂岩和深灰色泥岩不等厚互层组成。东营组是重要的油气产层, 储集层主要为三角洲平原分流河道和三角洲前缘河口坝沉积(朱红涛等, 2011)。分流河道砂体具有向上变细的正韵律, 而河口坝则为向上变粗的反韵律。东营组砂岩以成分成熟度低的岩屑质长石砂岩和岩屑砂岩为主, 分选中等, 颗粒为次圆— 次棱角状。

渤中凹陷东营组砂岩储集层质量差异很大。弄清楚导致差异的原因, 对优质储集层预测有重要指导意义。在此演示如何采用作者提出的方法, 计算出该砂岩储集层质量的主控因素。

本次选取了研究区W3井和W1井这2口井的砂岩岩心。W3井的砂岩为东营组二段上亚段(简称东二上)三角洲平原分流河道沉积; W1井的砂岩为东营组二段下亚段(简称东二下)三角洲前缘河口坝沉积。这2口井相离10, km。实测表明, 两者的渗透率差异很大( 表 2)。这种差异主要是沉积微相差异引起的还是成岩差异引起的?哪些单因素是主控因素?现分析如下:

对2个微相的砂岩岩心都各采多块样品, 并对每块样品进行孔隙度和渗透率分析、粒度分析、X射线衍射分析、铸体薄片分析、扫描电镜分析, 得到粒度、磨圆度、黏土杂基含量、黏土胶结物含量、非黏土胶结物含量、溶蚀孔隙含量和原生粒间孔含量等参数( 表 2)。然后, 根据多块样品的分析数据, 对每种微相的砂岩求取各个参数的平均值, 用来进行渗透率的计算。用平均值可以消除一些误差, 比只用1块样品更具有代表性。

表2 渤中凹陷东营组取心段各参数 Table2 Parameters of cores analysis in the Dongying Formation in Bozhong sag

从 表2中可知, 这2个微相的砂体各参数差异较大。分流河道砂岩的平均孔隙度为27.2%, 平均渗透率(k1)为1303.0× 10-3μ m2, 属于高孔高渗; 河口坝砂岩的平均孔隙度为21.5%, 平均渗透率(k2)为22.2× 10-3μ m2, 属于中孔低渗。分流河道砂岩与河口坝砂岩的实测渗透率平均值的比值为:

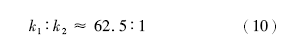
利用 表2中相关参数的平均值, 依据式(1), 计算得出分流河道砂岩与河口坝砂岩的理论渗透率比值为:

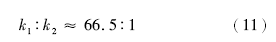
理论渗透率比值与实测渗透率比值非常接近, 表明样品测定的相关参数是准确可靠的。可以用来进行单因素贡献率以及沉积和成岩综合贡献率分析。

2.1 沉积单因素影响分析

2.1.1 黏土杂基对储集层质量的贡献率 分流河道砂岩和河口坝砂岩的黏土杂基含量分别为0.07%和2.09%( 图 1-a)。如果除了杂基含量外, 假定分流河道砂岩其他参数都与河口坝砂岩都相同, 即不含杂基时两者埋藏压实后的孔隙度都为15.7%(现今河口坝孔隙度21.5%减去溶蚀孔隙度5.8%得到, 溶蚀孔隙度计算参见石良等, 2015b), 等效粒径都为46.1, μ m, 颗粒都为次棱状, 假定没有后期胶结作用和溶蚀作用的影响, 然后看黏土杂基含量差异会导致多大的渗透率差异。

图1 渤中凹陷东营组分流河道与河口坝砂岩沉积单因素参数Fig.1 Sedimentary factors values of channel sandstone and mouth bar sandstone in the Dongying Formation in Bozhong sag

利用 表1中参数, 结合本区块东营组黏土X衍射分析, 可计算得出两类砂岩中黏土的比表面积约为37.6, m2/g, 用式(7)计算得出分流河道和河口坝砂岩的比表面分别为0.19, μ m-1和1.11, μ m-1。含杂基后, 分流河道和河口坝砂岩的孔隙度分别为15.6%和13.6%。将两者的孔隙度和比表面带入式(1), 可得到分流河道与河口坝砂岩的理论渗透率比值为:

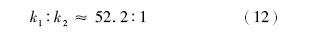
以上结果表明, 黏土杂基含量这一单因素的差异, 可导致渗透率的差异非常大, 分流河道砂岩的理论渗透率约是河砂坝52倍。

杂基含量差异对理论渗透率差异的贡献率为:

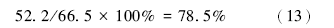
2.1.2 粒度对储集层质量的影响程度 粒度用等效粒径表征, 据公式(4)可计算出等效粒径。分流河道砂岩与河口坝砂岩的等效粒径分别为72.0, μ m、46.1, μ m( 图 1-b)。如果除了等效粒径不同外, 其他参数都相同, 那么等效粒径差异主要导致砂体比表面(S)不同, 用式(7)计算得出分流河道与河口坝砂体的比表面(S)分别为0.075, μ m-1、0.129, μ m-1。代入式(1), 可得分流河道与河口坝砂体的理论渗透率比值为:

以上结果表明, 等效粒径(粒度)这一单因素的差异, 可导致渗透率约2倍的差异。

粒度差异对理论渗透率差异的贡献率为:

2.1.3 分选系数对储集层质量的影响程度 根据粒度分析资料和分选系数计算公式, 分流河道与河口坝砂体的分选系数分别为1.67和1.65( 图 1-c)。同样, 如果只有分选系数不同而其他因素相同, 那么根据相关公式计算, 分流河道与河口坝砂岩的理论渗透率比值为1.01︰1, 基本没有差别。

分选系数差异对理论渗透率差异的贡献率为:

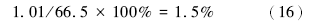
综合对比上述沉积作用3个单因素分析结果(式13、式15和式16), 可判别出黏土杂基对渗透率影响最大, 而分选系数的影响相对最小, 3个单因素的影响性从大到小顺序为黏土杂基→ 粒级大小→ 分选系数。

2.2 成岩作用因素分析

本区东营组砂岩的成岩作用的主要是胶结、溶蚀和压实。胶结作用使砂岩孔隙中充填了自生黏土矿物胶结物和碳酸盐胶结物, 溶蚀作用产生了次生溶蚀孔隙, 压实作用造成原生孔隙度减少( 图 2)。

图2 渤中凹陷东营组分流河道与河口坝砂岩成岩作用单因素参数Fig.2 Diagenetic factors values of channel sandstone and mouth bar sandstone in the Dongying Formation in Bozhong sag

2.2.1 自生黏土矿物对储集层质量影响程度

研究区自生黏土矿物有高岭石、伊利石、伊/蒙混层和绿泥石( 图 3-d— 3-h)。自生黏土矿物与黏土杂基的主要区别, 在于自生黏土矿物的晶形相对完好( 图 3-e— 3-h)。自生黏土矿物的晶体之间可以被环氧树脂充注( 图 3-d), 表明这些晶体之间的孔隙可以使流体(水、石油)通过, 可形成有效储集空间, 这与碳酸盐胶结物晶间无有效孔隙截然相反( 图 3-a, 3-b)。自生黏土矿物具有的湿水面积远远大于临近相对光洁的颗粒的湿水面积( 图 3-e, 3-f), 即具有非常大的比表面。

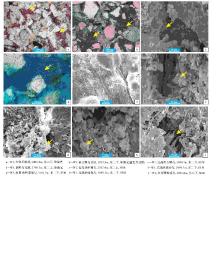图3 渤中凹陷东营组砂岩主要胶结物特征Fig.3 Characteristics of main cement in sandstones of the Dongying Formation in Bozhong sag

研究区自生黏土矿物通过2个途径来影响渗透率:一是充填孔隙, 减少孔隙度; 二是增大砂岩比表面。本区分流河道砂岩与河口坝砂岩自生黏土矿物的含量分别是0.15%和1.46%( 图 2-a)。除了自生黏土矿物含量外, 如果假定其他参数相同可以计算出的渗透率比值为:

自生黏土矿物含差异对理论渗透率差异的贡献率为:

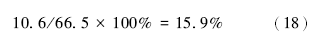
2.2.2 碳酸盐胶结物对储集层质量的影响程度

碳酸盐胶结物主要是充填孔隙, 减少孔隙度, 从而影响渗透率。分流河道砂岩与河口坝砂岩的碳酸盐胶结物含量分别是0.18%和2.22%( 图 2-a), 如果其他因素相同, 那么通过计算得出的渗透率比值为:

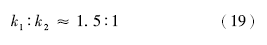
碳酸盐胶结物含量差异对理论渗透率差异的贡献率为:

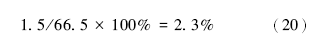
2.2.3 次生溶孔对储集层质量的影响程度

根据薄片统计和相关公式计算, 分流河道砂岩与河口坝砂岩的次生溶孔孔隙度分别为10.4%和11.4%( 图 2-b)。如果其他因素相同, 那么计算得出分流河道砂岩与河口坝砂岩的渗透率比值为:

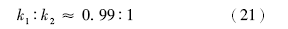
次生溶孔含量差异对理论渗透率差异的贡献率为:

2.2.4 压实作用的影响

压实导致孔隙度降低。根据薄片统计和相关公式, 计算出分流河道砂岩与河口坝砂岩的压实净孔率( 图 2-c)。如果其他因素相同, 压实净孔率的差异导致的渗透率比值约为:

压实差异对理论渗透率差异的贡献率为:

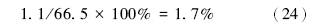
对比上述成岩作用的4个单因素分析结果(式18、式20、式22、式24), 可知:自生黏土矿物的差异对渗透率造成影响最大, 而次生溶孔影响最小, 相对影响从大到小顺序为自生黏土矿物→ 非黏土矿物胶结物→ 压实作用→ 次生溶孔。

2.3 沉积和成岩因素的综合贡献率

沉积因素的综合贡献率为各沉积单因素的贡献率之和, 即黏土杂基贡献率+粒度贡献率+分选系数贡献率:

成岩因素的综合贡献率为各成岩单因素的贡献率之和, 即自生黏土胶结物贡献率+碳酸盐胶结物贡献率+溶孔贡献率+压实贡献率:

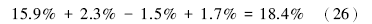
严格说来, 沉积综合贡献率+成岩综合贡献率应该为100%, 但由于各单因素实测中存在误差, 两者之和接近100%。

上述分析表明, 本区分流河道砂岩与河口坝砂岩渗透率的差异主要是沉积差异导致的, 沉积相是储集层质量的主控因素。

3 讨论

作者提出的单因素比较法优点包括:(1)能够确定各种沉积和成岩因素对储集层质量的具体贡献率, 使确定主控因素并据此作出精确预测成为可能。(2)多数情况下, 只需根据薄片分析, 就可以求出相关参数(包括粒度分析参数), 计算出砂岩孔隙度和渗透率, 而不需进行复杂、费时的岩心实测。(3)测井尽管可以较准确地分析出储集层的孔隙度, 但其渗透率分析误差很大。利用本方法, 可以利用岩屑的镜下和粒度分析等, 计算出储集层渗透率, 能极大节约成本。(4)可以计算未固结的现代沉积的渗透率, 为比较各类相的储集物性提供了基础。

本方法的缺点:利用薄片观察求取相关参数时, 有一定人为因素, 不同的人估算的数值可能有差异, 因此需要经验丰富的人来观察。

4 结论

1)渗透率单因素比较法可以用来确定各种沉积和成岩因素对储集层质量的具体贡献率, 可靠且易操作, 使确定储集层质量主控因素并据此作出精确预测成为可能。

2)渗透率理论计算方法精确度高, 应用广泛, 不仅可以节约成本和时间, 而且可以在不可能或不方便实测渗透率的情况下, 求取储集层渗透率。很多情况下, 可以仅根据薄片观察分析, 通过理论计算来求取砂岩渗透率。在井下, 可以根据岩屑用渗透率理论计算方法求取未取心井段储集层渗透率。

3)现代沉积研究中, 可以利用理论计算方法求取未固结砂质沉积物的渗透率, 比较不同相带对储集层质量的影响。

(责任编辑 郑秀娟)

作者声明没有竞争性利益冲突.

作者声明没有竞争性利益冲突.

参考文献
1 董月霞, 杨赏, 陈蕾, 王琦, 曹中宏. 2014. 渤海湾盆地辫状河三角洲沉积与深部储集层特征: 以南堡凹陷南部古近系沙一段为例. 石油勘探与开发, 41(4): 385-392.
[Dong Y X, Yang S, Chen L, Wang Q, Cao Z H. 2014. Braided river delta deposition and deep reservoir characteristics in Bohai Bay Basin: A case study of Paleogene Sha 1 Member in the south area of Nanpu Sag. Petroleum Exploration and Development, 41(4): 385-392] [文内引用:1]
2 付晶, 吴胜和, 罗安湘, 张立安, 李桢, 李继宏. 2013. 鄂尔多斯盆地陇东地区延长组纵向储集层质量差异及主控因素分析. 地学前缘, 20(2): 98-107.
[Fu J, Wu S H, Luo A X, Zhang L A, Li Z, Li J H. 2013. Reservoir quality and its controlling factors of Chang 8 and Chang 6, members in Longdong Area, Ordos Basin. Earth Science Frontiers, 20(2): 98-107] [文内引用:1]
3 傅强, 夏庆龙, 周心怀, 王根照, 李建平, 王清斌. 2010. 渤中凹陷古近系沙河街组相对高孔渗储集层成因分析: 以 QHD35-2-1井为例. 中国海上油气, 22(4): 221-224.
[Fu Q, Xia Q L, Zhou X H, Wang G Z, Li J P, Wang Q B. 2010. A genetic analysis of the reservior with relatively higher porosity and permeability in Paleogene Shahejie Formation, Bozhong sag: A case of Well QHD35-2-1. China Offshore Oil and Gas, 22(4): 221-224] [文内引用:1]
4 胡作维, 李云, 黄思静, 吕杰, 朱邴光. 2012. 砂岩储集层中原生孔隙的破坏与保存机制研究进展. 地球科学进展, 27(1): 14-25.
[Hu Z W, Li Y, Huang S J, Lü J, Zhu B G. 2012. Reviews of the destruction and preservation of primary porosity in the sand stone reservoirs. Advances in Earth Science, 27(1): 14-25] [文内引用:1]
5 金振奎, 刘春慧. 2008. 黄骅坳陷北大港构造带储集层成岩作用定量研究. 石油勘探与开发, 35(5): 581-587.
[Jin Z K, Liu C H. 2008. Quantitative study on reservoir diagenesis in northern Dagang structural belt, Huanghua depression. Petroleum Exploration and Development, 35(5): 581-587] [文内引用:1]
6 金振奎, 苏奎, 苏妮娜. 2011. 准噶尔盆地腹部侏罗系深部优质储集层成因. 石油学报, 32(1): 25-31.
[Jin Z K, Su K, Su N N. 2011. Origin of Jurassic deep burial high-quality reservoirs in the central Junggar Basin. Acta Petrolei Sinica, 32(1): 25-31] [文内引用:1]
7 石良, 金振奎, 闫伟, 李桂仔, 田玉昆. 2015 b. 异常高压对储集层溶蚀及成岩阶段的影响机理: 以渤中凹陷西北次凹为例. 中国矿业大学学报, 44(2): 262-270.
[Shi L, Jin Z K, Yan W, Li G Z, Tian Y K. 2015 b. Influence mechanism of abnormal high pressure on reservoir dissolution and diagenetic stage: An example from northwestern Bozhong sag. Journal of China University of Mining & Technology, 44(2): 262-270] [文内引用:1]
8 石良, 金振奎, 闫伟, 朱小二, 许新明, 彭飚. 2015 a. 异常高压对储集层压实和胶结作用的影响: 以渤海湾盆地渤中凹陷西北次凹为例. 石油勘探与开发, 42(3): 310-318.
[Shi L, Jin Z K, Yan W, Zhu X E, Xu X M, Peng B. 2015 a. Influences of overpressure on reservoir compaction and cementation: A case from northwestern subsag, Bozhong sag, Bohai Bay Basin, East China. Petroleum Exploration and Development, 42(3): 310-318] [文内引用:1]
9 谢润成, 周文, 晏宁平, 宁荣彩, 赵安坤, 王辛. 2010. 致密低渗砂岩储集层质量控制因素研究: 以靖边气田盒 8段为例. 石油实验地质, 32(2): 120-123.
[Xie R C, Zhou W, Yan N P, Ning R C, Zhao A K, Wang X. 2010. Study on control factors of quality of compact sand stone reservoir: Taking He8 formation of the Jingbian gas field as an example. Petroleum Geology & Experiment, 32(2): 120-123] [文内引用:1]
10 王京, 赵彦超, 刘琨, 王家豪. 2006. 鄂尔多斯盆地塔巴庙地区上古生界砂岩储集层 “酸性+碱性”叠加溶蚀作用与储集层质量主控因素. 地球科学, 31(2): 221-228.
[Wang J, Zhao Y C, Liu K, Wang J H. 2006. Superimposing controls of acidic and alkaline dissolutions on sand stone reservoir quality of the Paleozoic Xia Shihezi and Shanxi Formations in Tabamiao Area, Ordos Basin. Earth Science, 31(2): 221-228] [文内引用:1]
11 王瑞飞, 孙卫. 2009. 储集层沉积—成岩过程中物性演化的主控因素. 矿物学报, 29(3): 399-404.
[Wang R F, Sun W. 2009. Main factors controlling the evolution of physical properties during the process of reservoir sedimentation diagenesis. Acta Mineralogica Sinica, 29(3): 399-404] [文内引用:1]
12 严宗毅. 2002. 低雷诺数流理论. 北京: 北京大学出版社, 462-467.
[Yan Z Y. 2002. Low Renold Number Seepage Theory. Beijing: Peking University Press, 462-467] [文内引用:1]
13 杨玉卿, 潘福熙, 田洪, 徐晋, 陈力群. 2010. 渤中25-1油田沙河街组低孔低渗储集层特征及分类评价. 现代地质, 24(4): 685-693.
[Yang Y Q, Pan F X, Tian H, Xu J, Chen L Q. 2010. Characteristics and classification and evaluation of low porosity and permeability reservoir in Shahejie formation of BZ25-1 oil field. Geoscience, 24(4): 685-693] [文内引用:1]
14 郑占, 吴胜和, 许长福, 岳大力, 王伟, 张锋. 2010. 克拉玛依油田六区克下组冲积扇岩石相及储集层质量差异. 石油与天然气地质, 31(4): 463-471.
[Zheng Z, Wu S H, Xu C F, Yue D L, Wang W, Zhang F. 2010. Lithofacies and reservoirs of alluvial fan in the Lower Keramay Formation in the block-6 of Karamay oilfield, the Junggar Basin. Oil & Gas Geology, 31(4): 463-471] [文内引用:1]
15 朱红涛, 杨香华, 周心怀, 李建平, 王德英, 李敏. 2011. 基于层序地层学和地震沉积学的高精度三维沉积体系: 以渤中凹陷西斜坡BZ3-1区块东营组为例. 地球科学, 36(6): 1073-1084.
[Zhu H T, Yang X H, Zhou X H, Li J P, Wang D Y, Li M. 2011. High resolution three-dimensional facies architecture delineation using sequence straitigraphy, seismic sedimentology: Example from Dongying Formation in BZ3-1 block of western slope of Bozhong sag, Bohai Bay Basin. Earth Science, 36(6): 1073-1084] [文内引用:1]
16 Arnepalli D N, Shanthakumar S, Rao B H, Singh D N. 2008. Comparison of methods for determining specific-surface area of fine-grained soils. Geotechnical and Geological Engineering, 26(2): 121-132. [文内引用:1]
17 Blake F C. 1922. The resistance of packing to fluid flow. Transactions of the American Institute of Chemical Engineers, 14: 415-421. [文内引用:1]
18 Carman P C. 1937. Fluid flow through granular beds. Transactions-Institution of Chemical Engineeres, 15: 150-166. [文内引用:2]
19 Carrier Ⅲ W D. 2003. Goodbye, hazen;hello, kozeny-carman. Journal of Geotechnical and Geoenvironmental Engineering, 129(11): 1054-1056. [文内引用:3]
20 Childs E C, Collis-George N. 1950. The permeability of porous materials. Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, 201: 392-405. [文内引用:1]
21 Churchman G J, Burke C M. 1991. Properties of sub soils in relation to various measures of surface area and water content. Journal of Soil Science, 42(3): 463-478. [文内引用:2]
22 Ehrenberg S N. 1990. Relationship between diagenesis and reservoir quality in sand stones of the Garn Formation, Haltenbanken, Mid-Norwegian Continental Shelf. AAPG Bulletin, 74(10): 1538-1558. [文内引用:1]
23 Fair G M, Hatch L P, Hudson H E. 1933. Fundamental factors governing the streamline flow of water through sand [with discussion]. Journal of American Water Works Association, 25(11): 1551-1565. [文内引用:2]
24 Jong E. 1999. Comparison of three methods of measuring surface area of soils. Canadian Journal of Soil Science, 79(2): 345-351. [文内引用:1]
25 Loudon A G. 1952. The computation of permeability from simple soil tests. Geotechnique, 3(4): 165-183. [文内引用:1]
26 Metz V, Raanan H, Pieper H. 2005. Towards the establishment of a reliable proxy for the reactive surface area of smectite. Geochimica et Cosmochimica Acta, 69(10): 2581-2591. [文内引用:1]
27 Petersen L W, Moldrup P, Jacobsen O H, Rolston D E. 1996. Relations between specific surface area and soil physical and chemical properties. Soil Science, 161(1): 9-21. [文内引用:1]
28 Rossi C, Marfil R, Ramseyer K, Permanyer A. 2001. Facies-related diagenesis and multiphase siderite cementation and dissolution in the reservoir sand stones of the Khatatba Formation, Egypt's Western Desert. Journal of Sedimentary Research, 71(3): 459-472. [文内引用:1]
29 Salem A M. 2005. Diagenesis and reservoir-quality evolution of incised-valley sand stones: Evidence from the Abu Madi gas reservoirs(Upper Miocene), The Nile Delta Basin, Egypt. Journal of Sedimentary Research, 75(4): 572-584. [文内引用:1]
30 Salem A M, Morad S, Mato L F, Al-Aasm I S. 2000. Diagenesis and reservoir-quality evolution of fluvial sand stones during progressive burial and uplift: Evidence from the Upper Jurassic Boipeba Member, Reconcavo Basin, Northeastern Brazil. AAPG Bulletin, 84(7): 1015-1040. [文内引用:1]
31 Scherer M. 1987. Parameters influencing porosity in sand stones: A model for sand stone porosity prediction. AAPG Bulletin, 71(5): 485-491. [文内引用:1]
32 Yukselen Y, Kaya A. 2006. Comparison of methods for determining specific surface area of soils. Journal of Geotechnical and Geoenvironmental Engineering, 132(7): 931-936. [文内引用:1]