李向东. (2022)波—流相互作用机制与复合流的沉积构造鉴别标志* [J]. 古地理学报, 24(1): 45-60
Li Xiang-Dong. (2022)Mechanism of wave-current interaction and identification of sedimentary structures of combined-flow[J]. Journal Of Palaeogeography, 24(1): 45-60.   
Doi: 10.7605/gdlxb.2022.01.004
Permissions
Copyright©2022, 《古地理学报》编辑部
版权所有.《古地理学报》编辑部
波—流相互作用机制与复合流的沉积构造鉴别标志*
李向东
昆明理工大学国土资源工程学院,云南昆明 650093

作者简介:李向东,男,1973年生,毕业于长江大学,获博士学位,现为昆明理工大学国土资源工程学院副教授,主要从事沉积学研究。E-mail: lixiangdong614@163.com。

收稿日期:2021-05-14
基金资助:*自然资源部深地动力学重点实验室开放课题基金(编号: J1901-16)及国家自然科学基金项目(编号: 41272119)共同资助
摘要

波—流相互作用是复杂水动力条件下流体相互作用的主要方式之一,由波—流相互作用形成的复合流沉积是目前沉积学在流体相互作用这一领域研究较多的一种沉积类型。以已有的文献为基础,对波—流相互作用下细砂级颗粒的运动机制进行了综述,预测了波—流相互作用的沉积特征,总结了复合流的沉积构造鉴别标志。取得的主要认识有: ( 1)波—流相互作用总体上属于衰弱流( waning flow)悬浮沉积,其微观的沉积机制可分为 5种: 越过崩落点的喷射沉积( S1)、残余涡动沉积( S2)、未到崩落点的喷射沉积( S3)、背流面的崩落沉积( S4)、垂直降落沉积( S5);( 2)波—流相互作用的沉积过程总体上受悬砂量和沉积时间的控制, 5种微观沉积机制在不同的悬砂量和沉积时间条件下可形成不同的沉积机制组合,从而导致不同的底床形态;( 3)复合流沉积构造鉴别标志主要有: 复合流波痕、复合流层理、爬升型复合流层理、不对称丘状交错层理、准平行层理和频繁交替的不能充分发育的浪成波纹层理与流水层理等 6类。上述认识对于复杂水动力条件下的沉积学研究及对深水、浅水沉积环境的识别均具有重要的意义。

关键词: 波—流相互作用;; 复合流沉积; 丘状交错层理; 沉积构造; 沉积机制
中图分类号:P512.2 文献标志码:A 文章编号:1671-1505(2022)01-0045-16
Mechanism of wave-current interaction and identification of sedimentary structures of combined-flow
Li Xiang-Dong
School of Land Resource Engineering, Kunming University of Science and Technology, Kunming 650093,China
Fund:Fund：[Co-funded by the Key Laboratory of Deep-Earth Dynamics of Ministry of Natural Resources(No. J1901-16)and the National Natural Science Foundation of China(No.41272119)]
Abstract

Wave-current interaction is one of the main types of flow interaction under complex hydrodynamic system,and the deposits of combined flow affected by wave-current interaction is one of the common sedimentary types studied in this area. In this paper,the movement mechanism of fine-grained sand and the sedimentary features under the wave-current interaction are reviewed and predicted,and the identification characteristics of sedimentary structures of combined-flow are summarized. The main conclusions include: (1)wave-current interaction leads to the waning flow suspended deposits in general. The microsedimentary mechanism include: the spray deposit beyond brink point(S1),residual vortex deposit(S2),the spray deposit under brink point(S3),avalanching deposit in the lee side(S4),vertical falling deposit(S5);(2)deposition processes under wave-current interaction are mainly controlled by the suspended sand amount and the deposition time,and the five sedimentary mechanisms resulted in different deposition associations and different morphologies of sea bed;(3)the identification on sedimentary structures of combined flow include: combined-flow ripple,combined-flow-ripple lamination,climbing combined-flow-ripple lamination,asymmetry hummocky cross-bedding,quasi-planar lamination,and frequent alternation of wave-ripple and current-ripple bedding. The studies in this paper are significant for understanding the sedimentology under complex hydrodynamic conditions and the identification of deep-water and shallow water sedimentary environments.

Key words: wave-current interaction; combined-flow deposits; hummocky cross-bedding; sedimentary structure; deposition mechanism

开放科学(资源服务)标识码(OSID)：

波— 流相互作用是非线性科学的前沿课题。在海洋物理学中, 主要包括波浪在水流中的变形、波— 流相互作用对流场的影响、波和流与结构物的相互作用以及波流边界层等问题(王涛和李家春, 1999; Singh and Debnath, 2016)。在大气科学中, 常把一个物理量分解成基本态和被称为“ 波” 的扰动态, 两者之间的相互作用可以称为波— 流相互作用(徐祥德和冉令坤, 2007)。这2种研究方法的实质是相同的, 前者是从流体叠加的角度来研究, 后者是对复杂流动进行波、流分离。文中结合沉积学的研究现状, 从流体叠加的角度对波— 流作用在沉积学中的应用进行初步的探索。

从沉积学的角度讲, 波— 流相互作用主要存在于复杂水动力条件下, 其中复杂水动力条件是指由流动(如河流、异重流、浊流、地转流等)引起的单向流、由短周期波动(如风暴、海面波浪、随机内波、孤立内波等)引起的振荡流以及由长周期波动(如潮汐、内潮汐、海啸等)引起的双向交替流动等相互作用而形成的沉积水动力条件(Hill et al., 2003; 李向东等, 2010; Patacci et al., 2014; Felletti et al., 2016)。波— 流相互作用的基本作用方式(李向东, 2020a)主要有振荡流与单向流相互作用(波— 流作用)、振荡流与振荡流相互作用(波— 波作用)和单向流与单向流相互作用(流— 流作用)。目前在沉积学研究中, 波— 波作用和流— 流作用研究相对较少, 如对驻波沉积问题(Prave and Duke, 1990; 师庆民等, 2013)和浊流反射问题(Patacci et al., 2014; Tinterri et al., 2016)的研究, 而研究相对较多的则是由波— 流相互作用形成的复合流(combined-flow)沉积。

复合流是指2种或多种不同类型的流体在时间上和空间上的叠加, 但一般情况下, 将用于叠加的流体限定为单向流和振荡流(Dumas et al., 2005)。复合流的研究起源于对沉积物波痕形成水动力条件的水槽实验研究(Harms 1969), 在复合流水动力条件下, 观察到的波痕具有不对称且光滑的波峰及上凸或曲线型的纹层, 其厚度呈在波峰处变薄、在波谷处变厚的特征, 这既不同于流水波痕, 也不同于浪成波痕。在地层记录中, 首先基于对现代沉积物的观察, 提出了丘状交错层理的复合流成因机制(Greenwood, 1986; Nø ttvedt and Kreisa, 1987), 其后对与风暴沉积有关的丘状交错层理和与浊流沉积相关的似丘状交错层理成因进行了较深入的研究, 进一步确认了复合流参与的重要性(Dumas et al., 2005; Dumas and Arnott, 2006; Basilici et al., 2012; 李向东, 2020a), 并在近年来成为了研究热点(钟建华等, 2016; 王家豪等, 2017; 许安涛等, 2018; 张昊等, 2019)。目前, 复合流已成为流体相互作用的一种重要类型(李向东, 2020a), 已发现的复合流沉积就流体类型而言, 主要有风暴引起的波浪与地球自转科氏力引起的地转流及三角洲环境中的洪水、异重流等(Li and Amos, 1999; Hill et al., 2003; Bowman et al., 2014; Collins et al., 2017; Paz et al., 2019), 波浪与潮汐(Molgat and Arnott, 2001; Wu and Parsons, 2019), 波浪与浊流及富泥密度流等(Myrow et al., 2002; Plint et al., 2012; Harazim and Mcilroy, 2015), 短周期内波与低密度浊流(李向东等, 2010; Pomar et al., 2019)以及浊流反射形成的内波等(Tinterri et al., 2016; 李向东等, 2019)。

目前所研究的复合流沉积实质是在波— 流相互作用下形成的沉积, 而不是对已有沉积物的改造。复合流发育的环境主要为具有复杂水动力条件的潮坪、河口湾、三角洲前缘、海滩、陆棚及大洋(Dumas et al., 2005; Perillo et al., 2014; 李向东等, 2020a)。文中以振荡流和复合流水槽实验研究资料为基础, 结合有关复合流的沉积学研究, 着重探讨波— 流相互作用机制, 并总结复合流的沉积构造鉴别标志, 这对于复杂水动力条件下的沉积学研究及对深水、浅水沉积环境的识别均具有重要的意义。

图 1 波— 流相互作用框架图
a— 波— 流叠加形成的复合流分类; b— 波— 流相互作用方式Fig.1 Frame chart for interaction of wave and current

1 波— 流相互作用的沉积学分类

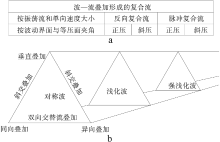
在波— 流作用中可能会有2种情况: 一是先存在单向流, 再叠加波动, 相当于海洋物理学中剪切流背景下的波动问题; 二是先有波动存在, 再叠加单向流。这2种情况可能会有所差别, 但在沉积学里可暂不考虑。波— 流相互作用形成的复合流按振荡流和单向流的相对速度大小可分为反向复合流和脉动复合流2大类(图 1-a), 反向复合流是指当波浪的轨迹速度大于单向流速度时, 在1个波动周期内, 复合流的流动方向会发生反转; 脉动复合流是指当波浪的轨迹速度小于单向流速度时, 在1个波动周期内, 复合流始终流向同一方向, 只是速度大小发生周期性的变化(Lamb et al., 2008)。此外, 在沉积学研究中, 特别是在深水环境下内波、内潮汐沉积的研究中, 波动的斜压问题也引起了关注(Davie et al., 1988; 李向东, 2013), 按照波动界面(即海水密度或温度界面)是否与海平面(在海洋学研究中可近似地将海平面看作等压面)存在夹角(界面波)或波动是否平行海平面传播(体波), 可进一步分为正压反向复合流、斜压反向复合流、正压脉动复合流和斜压脉动复合流4小类(图 1-a)。一般情况下表面波多为正压波, 内波多为斜压波, 但是当短周期内波的频率接近浮力频率(指在密度层结稳定的海洋中, 海水微团受到某种力的干扰后, 在铅直方向上自由振荡的频率)时, 内波的传播方向接近水平方向(方欣华和杜涛, 2004), 此种情况则可作为正压波来处理。

对每一种复合流类型, 还可进一步按单向流与振荡流的叠加方式和波动类型进行细分。在波— 流相互作用中, 单向流与振荡流的叠加方式有4种, 即与波动的传播方向相向叠加、异向叠加、垂直叠加和呈一定的角度叠加(Davies et al., 1988)。在4种叠加方式中, 取同向叠加、异向叠加、垂直叠加为3个端元组成三角形的3个顶点, 则与垂直叠加相邻的2条边可代表呈一定的角度叠加(斜交叠加), 同向叠加与异向叠加之间的边则可代表双向交替流与波动叠加的情形(图 1-b), 最后以参与波— 流叠加的波动类型分为与对称波叠加、与浅化波叠加和与强浅化波叠加3类(图 1-b)。

由于单向流对振荡流边界层的速度、剪切力和紊流能量的影响趋势一致, 只是在空间分布上有所差异, 在垂直叠加和斜交叠加中会出现沿一定方向的“ 蝴蝶” 状分布(非原路径的往返)。因此, 4种叠加方式中颗粒的剥蚀、悬浮和沉积机制基本一致, 差异只在叠加后的能量大小和运动方向上(Davies et al., 1988; Raushan et al., 2018; Wu and Parsons, 2019)。鉴于沉积学的研究现状, 文中只探讨相向叠加和异向叠加2种。

2 细砂级颗粒运动机制
2.1 复合流中砂粒的微观沉积机制

关于砂粒在振荡流和复合流中的运动研究已有不少文献, 包括理论探讨、实验和野外观测, 将这些文献的成果综合起来, 主要有以下几点: (1)在理想条件下(流体粘滞力足够小), 只要有振荡流存在(或含振荡流分量), 就会形成涡流, 并将侵蚀的砂粒卷入涡流, 形成“ 砂云” (Sand cloud)(Davie et al., 1988; Yokokawa et al., 1995; 林缅和袁志达, 2005; Ribberink et al., 2007)。(2)砂云在振荡流衰弱阶段(速度随时间变小)发生喷射(burst)沉积, 砂云发生喷射沉积时在垂向上的位置高低(是否高于崩落点)及在横向上的位置(底床的波峰、波谷、迎流面和背流面)则和振荡流的强度、周期、对称性(波浅化程度)及单向流的强度、方向性等因素有关(Dumas et al., 2005; 林缅和袁志达, 2005; Zedler and Street, 2006; Yamaguchi and Sekiguchi, 2010; Raushan and Singh, 2018)。(3)复合流中单向流的存在, 当振荡流强度足够弱时(如振荡流转向时段)可在背流面形成崩落沉积, 但单向流的崩落沉积能否保存下来, 则和振荡流的周期、强度等因素有关(Yokokawa et al., 1995; Perillo et al., 2014a, 2014b; Singh and Debnath, 2016; Wu and Parsons, 2019)。(4)沉积时间的长短, 则影响着砂粒的降落沉积和残余砂云沉积: 当沉积时间较短时, 残余砂云会被转向后的流体带到相邻波峰, 在转向后流体的迎流面沉积, 形成残余砂云沉积; 当沉积时间较长时, 涡动将悬浮砂带不到流体转向, 则会在波谷附近发生砂粒的降落沉积(Yamaguchi and Sekiguchi, 2010; Perillo et al., 2014a, 2014b; Lu et al., 2017)。

根据上述文献的研究成果, 可将振荡流和复合流中涡流的微观沉积机制概括为以下5种类型: 越过崩落点的喷射沉积(S1)、残余涡动沉积(S2)、未到崩落点的喷射沉积(S3)、背流面的崩落沉积(S4)和垂直降落沉积(S5)。其涡流的形成及相关的微观沉积机制主要受底床上流体速度和作用时间(剥蚀或沉积)的影响, 在一定范围内, 作用时间的延长可补偿速度上的不足, 因此, 对复合流条件下涡流的形成及其微观沉积机制可定性地总结如下(图 2): (1) 当流体速度较小时, 由于实际流体的黏性及悬浮其中的沉积物颗粒的阻碍, 可不形成涡流; 此时的沉积以垂直降落沉积(S5)为主, 在沉积作用时间较长时可形成背流面崩落沉积(S4)。

(2)随着速度的增大, 在迎流面形成涡流(A), 但上一周期的残余涡流无法运行到波谷, 故随着进一步发展, 由涡流A在波谷处形成涡流C, 涡流C剥蚀底床, 形成砂云; 此时的沉积由越过崩落点的喷射沉积(S1)、残余涡动沉积(S2)和未到崩落点的喷射沉积(S3)组成。(3)随着速度的进一步增大, 上一周期的残余涡流在背流面沉积之后, 仍可运行至波谷, 波谷涡流(C)由迎流面涡流(A)和波谷残余涡流(B)合并而成; 此时的沉积主要由越过崩落点的喷射沉积(S1)和残余涡动沉积(S2)组成。(4)当速度相当大时, 可形成立轴旋涡; 其沉积在悬浮物较多时为丘状交错层理, 在悬浮物较少时为洼状交错层理(Dumas and Arnott, 2006; 李向东, 2020b)。

由于单向流的叠加, 使得复合流的边界层厚度大于相应的纯振荡流的边界层厚度, 而边界层厚度的增大有利于对振荡流所产生的涡动的抑制。在叠加过程中, 流体速度、剪切力和紊流能量变化如下(Davies et al., 1988; Wu and Parsons, 2019): (1)单向流的叠加对振荡流边界层底部的速度分布影响不大, 仅使速度的绝对值有所减小, 对边界层上部速度的不对称性影响明显, 明显偏向单向流方向。(2)同流动方向叠加, 边界层剪切力增大, 相反则减小, 边界层下部受振荡流控制, 上部则受单向流控制。(3)同流动方向叠加, 边界层紊流能量增大, 相反则减小, 单向流会使得紊流能量的最大值和最小值分别靠近速度的最大值和最小值(即单向流抑制涡流上升, 从而使沉积时间变长)。

图 2 振荡流存在条件下底床上涡流的形成与微观沉积机制示意图
a— 底床上涡流的类型与演化: A为迎流面涡流, B为波谷残余涡流, C为波谷涡流; b— 微观沉积机制类型与演化, HCS为丘状交错层理, SCS为洼状交错层理, S1为越过崩落点的喷射沉积, S2为残余涡流沉积, S3为未到崩落点的喷射沉积, S4为背流面的崩落沉积, S5为垂直降落沉积Fig.2 Formation and microscopic sedimentary mechanism of vortex above bed under combined-flow

2.2 振荡流中细砂级颗粒的运动机制

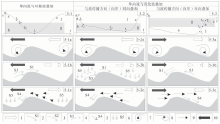
在探讨复合流砂粒运动之前, 先对砂粒在振荡流中的运动分析一下。振荡流是波浪与底床相互作用而产生的, 是海底床面附近的典型流动特征, 它是非定常的、空间结构复杂的流动, 包括流动边界层附近涡流的产生、脱落、合并及涡流强度的周期变化, 并在1个周期内出现涡流反向(林缅和袁志达, 2005), 可导致剥蚀与沉积的交替, 故可划分出剥蚀区(图 3中的Ⅰ )和沉积区(图 3中的Ⅱ )。在剥蚀区, 振荡流最大速度越大、剥蚀作用时间越长, 其剥蚀强度越大, 涡流的悬砂量越大; 在沉积区, 沉积作用强度主要受悬砂量和沉积作用时间的控制, 涡流中的悬砂量越大、沉积作用时间越长, 沉积作用强度就越大。此外, 剥蚀作用和沉积作用最强的时刻分别滞后于波峰时刻和波动转向时刻, 图 3中ta和tc为不同方向最大的剥蚀时刻, tb1和tb2分别为主要沉积时刻和剥蚀前沉积时刻(林缅和袁志达, 2005; Yamaguchi and Sekiguchi, 2010)。

图 3 纯振荡流在波状底床上1个波动周期内砂粒运动示意图
左边为向海岸方向; 右边为向海方向; v— 流体速度, 向岸为正, 向海为负; t— 时间; Ⅰ — 剥蚀区域, Ⅱ — 沉积区域; A— 迎流面涡流, B— 波谷残余涡流, C— 波谷涡流; ta— 为起动阶段最大剥蚀时刻, tc— 反向阶段最大剥蚀时刻, tb1— 沉积强度最大时刻, tb2— 剥蚀前沉积时刻。a— 起动阶段; b— 沉积阶段; c— 振荡流反向阶段(含剥蚀和沉积2个过程); 在沉积阶段(图 3-1b、3-2b和3-3b中): 实线为tb1时刻, 虚线为tb2时刻。图例中: 1— 振荡流方向与强度; 2— 越过崩落点的喷射沉积(S1); 3— 残余涡动沉积(S2); 4— 未到崩落点的喷射沉积(S3); 5— 背流面的崩落沉积(S4); 6— 垂直降落沉积(S5); 7— 强涡流; 8— 弱涡流; 9— 无涡流Fig.3 Schematics of sand movements on ripple surface during one wave period under pure oscillatory flow

由于波浪与海底相互作用可形成浅化波, 浅化波为尖的波峰且被宽的波谷分开, 在近底床产生不对称振荡流, 向岸为强的短程流动, 向海方向为弱的长程流动(Yamaguchi and Sekiguchi, 2010)。因此, 依据流速和流动时间的不对称性, 可将振荡流分为3种(图 3): 对称、弱浅化和强浅化(Zhang et al., 2011)。以下以水流方向由右向左(左边靠近海岸)为例, 其过程可分为起动阶段、沉积阶段和反向阶段, 反向之后的沉积阶段与起始阶段之后的沉积作用相似, 对于弱浅化波和强浅化波来说, 其沉积作用更弱。

在起动阶段, 对称型振荡流(图 3-1a)的水流会沿着底床迎水面“ 搓” 出一正涡A(逆时针方向), 而后A顺流迁移, 并逐渐增强, 到达下一波谷时, 与上半周期在该波谷处脱落的残余涡流B合并而形成波谷正涡C, 正涡C在波谷处侵蚀底床并将沙粒卷入涡流, 形成砂云(Zedler and Street, 2006); 弱浅化和强浅化振荡流与此类似(Yamaguchi and Sekiguchi, 2010), 只是在前1周期的反向阶段, 由于剥蚀速度较小, 没有形成强的涡流, 此时在波谷无残余涡流, 由涡流A独立发展成涡流C(图 3-2a, 3-3a), 涡流中的悬砂量也相对较少。随着水流速度的减小, 砂云随涡流上升, 并发生喷射沉积。

在波动转向前后的沉积阶段三者有所不同(图 3-1b, 3-2b, 3-3b): 对称波产生对称振荡流, 砂云随涡流上升, 在背流面近底床流场开始局部转向时(Ribberink et al., 2007), 下一波谷处(图 3-1b中迎流面左侧波谷)砂云越过崩落点(Yamaguchi and Sekiguchi, 2010), 在波顶及迎流面发生喷射沉积(林缅和袁志达, 2005; Zedler and Street, 2006), 在整个流场开始转向时(图 3-1中tb1时刻), 沉积作用最强(图 3-1b中S1); 此后, 随着近底床由上升流变为下降流(Zedler and Street, 2006; Ribberink et al., 2007), 上一波谷处(图 3-1b中迎流面右侧波谷)由原流形成的正涡开始在迎流面靠近该波谷处脱落也形成沉积(图 3-1b中S2)。对于弱浅化波(图 3-2b), 由于起动阶段时间变短, 反向后加速度变小, 即沉积时间变长(Yamaguchi and Sekiguchi, 2010), 部分砂粒会在未达到崩落点时在背流面发生喷射沉积(S3), 但大多数砂粒仍越过崩落点在波顶及迎流面形成沉积(S1), 同时也有上一波谷形成的残余涡流的脱落沉积(S2)。对于强浅化波(图 3-3b), 由于涡动剥蚀时间短, 而流体转向和加速需要的时间长, 涡动无法将悬浮的砂保持到流体变向, 多在背流面降落沉积(S5), 少数悬浮的砂也可在波顶沉积, 很少在迎流面沉积(Yamaguchi and Sekiguchi, 2010)。

在反向剥蚀阶段(图 3-1c, 3-2c, 3-3c): 对称波与起动阶段相同, 形成一个强的涡动(负涡), 其后沉积过程与前一过程类似(图 3-1c), 因此形成对称的底床形态; 又由于波峰附近为主要沉积场所(越过崩落点沉积S1), 而波谷附近以残余涡动沉积(S2)为主, 故纹层在波峰处变厚, 在波谷处变薄(Raaf et al., 1977; Dumas et al., 2005)。弱浅化波形成一个弱的负涡, 由于悬砂量的减少, 沉积时间又短(图 3-2c), 可能以未到崩落点的喷射沉积(S3)为主, 兼以越过崩落点沉积(S1), 故形成弱不对称的底床形态(Yamaguchi and Sekiguchi, 2010), 沉积物多沉积在波传播的反方向(波动未反转时的越过崩落点沉积和反转后的未到崩落点沉积), 即向海方向(图 3-2中向右), 但纹层倾角较大侧为波的传播方向(图 3-2中向左)。强浅化波由于转向后流速较小(Zhang et al., 2011)则不形成负涡(Yamaguchi and Sekiguchi, 2010), 其沉积为单向流背流面(向海方向)崩落沉积(图 3-3c), 但剥蚀量小, 沉积微弱, 其上一阶段的悬浮沉积多发生在向岸一侧, 故形成不对称(不对称程度大于复合流)且波峰光滑的底床形态(Yamaguchi and Sekiguchi, 2010), 纹层倾角大的一侧仍为波动传播方向(图 3-3中向左)。

2.3 复合流中细砂级颗粒运动机制

由于对称波与单向流叠加, 无论同向、异向(传播方向), 其过程相似(Lamb et al., 2008), 单向流在半个周期内和振荡流同向叠加, 在另半个周期内和振荡流异向叠加(振荡流流动方向), 因此笔者只考虑与波传播方向相向叠加的情况。对于浅化波, 弱浅化波的叠加介于对称波和强浅化波之间, 更接近于对称波(Christensen et al., 2019), 往往在1个周期内形成2次紊流和沉积物悬浮事件, 其强弱则与波的浅化程度(波歪度或不对称性)相关(Villard and Osborne, 2002), 强浅化波在1个周期内则往往只形成1次紊流和沉积物悬浮事件(Ruessink et al., 2011)。因此, 仅对单向流与强浅化波叠加的情况进行分析, 对于每一种复合流也分为3种情形: 与对称波传播方向同向叠加、与强浅化波传播方向同向叠加及与强浅化波传播方向异向叠加。

就微观机制来说, 振荡流与单向流的叠加是一个复杂的相互作用过程, 但就其宏观的作用效果来说, 依据现有的研究成果(Yokokawa et al., 1995; Li and Amos, 1999; Dumas et al., 2005; Yamaguchi and Sekiguchi, 2010; Perillo et al., 2014a; Lu et al., 2017; Raushan et al., 2018), 主要有以下3点: (1) 使边界层增厚, 抑制涡流发展, 从而影响剥蚀强度和涡流中的悬砂量; (2) 在不改变流速分布的情况下, 使叠加后的流速增大(同流动方向)或减小(异流动方向), 从而影响剥蚀强度和涡流的迁移速度(即沉积位置); (3)抛开复杂的流体质点微观作用机制, 叠加后的速度可通过平移横坐标的方法进行定性的分析(Davies et al., 1988; Lamb et al., 2008; Perillo et al., 2014b; Christensen et al., 2019)。基于上述3点, 对复合流中细砂级颗粒的运动机制作出定性的分析, 而在叠加过程中波长变大、波高变小及波峰区域变宽等现象(Wu and Parsons, 2019)暂不予考虑。

图 4 反向复合流在波状底床上1个波动周期内砂粒运动示意图
左边为向海岸方向; 右边为向海方向; v— 流体速度, 向岸为正, 向海为负; t— 时间; Ⅰ — 剥蚀区域, Ⅱ — 沉积区域; A— 迎流面涡流, B— 波谷残余涡流, C— 波谷涡流; ta— 为起动阶段最大剥蚀时刻, tc— 反向阶段最大剥蚀时刻, tb1— 沉积强度最大时刻, tb2— 剥蚀前沉积时刻。a— 起动阶段; b— 沉积阶段; c— 振荡流反向阶段(含剥蚀和沉积2个过程); 在沉积阶段(图 3-1b、3-2b和3-3b中): 实线为tb1时刻, 虚线为tb2时刻。图例中: 1— 振荡流方向与强度; 2— 越过崩落点的喷射沉积(S1); 3— 残余涡动沉积(S2); 4— 未到崩落点的喷射沉积(S3); 5— 背流面的崩落沉积(S4); 6— 垂直降落沉积(S5); 7— 强涡流; 8— 弱涡流; 9— 无涡流; 10— 单向流方向与强度Fig.4 Schematics of sand movements on ripple surface during one wave period under reversing combined-flow

2.3.1 反向复合流

在起动阶段, 对于和波动传播方向同向叠加(单向流从海向陆流动)而言(图 4-1, 4-2), 由于单向流与振荡流流动方向同向叠加会增加叠加后的速度(Davies et al., 1988), 但同时使边界层厚, 并造成悬浮颗粒的垂向浓度分层, 从而抑制涡流的发展(王涛和李家春, 1999), 因此在起始阶段水流先沿着底床迎水面“ 搓” 出一较强的正涡A(Yokokawa et al., 1995; Li and O’ Connor, 2007); 但反向阶段速度小、时间短, 形成的负涡不能保持到波谷(Li and O’ Connor, 2007), 故波谷不存在残余涡流, 波谷涡流C由涡流A独立发展而成(图 4-1a, 4-2a); 对称波剥蚀作用时间长, 涡流悬砂量较大(Lamb et al., 2008), 浅化波剥蚀作用时间短、速度小, 从而导致悬砂量较少(林缅和袁志达, 2005)。对于强浅化波异传播方向叠加而言(图 4-3), 在起始阶段形成的正涡A, 由于单向流与振荡流流动方向异向叠加, 使叠加后速度减小, 同时又抑制涡流的发展(Davies et al., 1988; 王涛和李家春, 1999), 故其强度较弱(图 4-3a); 但上半周期(单向流与振荡流流动方向相同)形成的负涡, 其形成时流体速度较大, 同时剥蚀作用时间长(图 4-3), 使得负涡强度较大, 再加之沉积时间较短, 残余涡流B会在波谷保存下来(Li and O’ Connor, 2007), 与正涡A合并, 形成相对较强的正涡C(图 4-3a); 涡流C在波谷处侵蚀底床并将沙粒卷入涡流, 形成砂云, 由于涡流的叠加, 其悬砂量较大(Yokokawa et al., 1995; Villard and Osborne, 2002)。

在沉积阶段(图 4-1b, 4-2b, 4-3b), 复合流沉积的5种沉积类型分布如下: (1)在对称波叠加中(图 4-1b), 由于单向流对涡流上升的抑制(Yokokawa et al., 1995), 主要由未到崩落点的喷射沉积(S3)、越过崩落点的喷射沉积(S1)和残余涡动沉积组成(S2), 在振荡流转向时, 由于单向流的作用, 会形成背流面的崩落沉积(S4), 但该沉积会被下一周期的涡流剥蚀而不能保存下来(Yokokawa et al., 1995); (2)在浅化波同向叠加中(图 4-2b), 由于受单向流向岸流动的影响, 剥蚀阶段同流向叠加, 剥蚀速度大, 转向后异流向叠加, 流体加速慢, 故在此阶段悬砂量较浅化波大, 沉积时间较浅化波长(图 3-3), 涡动无法将反向剥蚀阶段(见下文)悬浮的砂保持到流体转向, 因此不形成残余涡动沉积, 主要由未到崩落点的喷射沉积(S3)、越过崩落点的喷射沉积(S1)和波谷的垂直降落沉积(S5)组成, 同样, 波动转向时会在背流面形成崩落沉积(S4), 且由于反向阶段无涡流产生, 故有可能保存下来(图 4-2b); (3)在浅化波异向叠加中(图 4-3b), 由于受单向流向海流动的影响, 剥蚀阶段异流向叠加, 剥蚀速度小, 转向后同流向叠加, 流体加速快, 沉积时间较浅化波短(图 3-3; 图 4-3), 再加上单向流对振荡流在垂向上特别是边界层上部的抑制(Davies et al., 1988; Wu and Parsons, 2019), 主要在背流面形成未到崩落点的喷射沉积(S3), 并可在迎流面形成越过崩落点的喷射沉积(S1), 同时上半周期的残余涡动会部分保持到流体再次转向, 形成残余涡动沉积(S2)。

在反向剥蚀阶段(图 4-1c, 4-2c, 4-3c), 其涡动强度和剥蚀时间均有所变化。在与对称波叠加的反向复合流中, 此时单向流与振荡流方向相反, 形成一个弱的负涡(图 4-1c), 由于悬砂量的减少, 再沉积时将以未到崩落点沉积为主(Yokokawa et al., 1995), 故形成与弱浅化波类似的弱不对称的底床形态(Yokokawa et al., 1995; Li and O’ Connor, 2007), 纹层倾角较大侧为波的传播方向(图 4-1中向左)。在细砂级颗粒水槽实验中, 一般当单向流速度小于10 cm/s时才会形成对称底床(Arnott and Southard, 1990; Dumas et al., 2005; Perillo et al., 2014b)。但是当单向流速度超过颗粒的移动门限可产生剥蚀时, 也有可能形成对称底床(Perillo et al., 2014a), 故单向流的叠加对于反向剥蚀强度影响较大; 对于异向叠加, 即单向流从陆向海流动, 由于单向流的输运作用, 底床的不对称程度变大(Li and O’ Connor, 2007)。此外, 由于沉积时间短, 当振荡流速度变化较快时(短周期), 涡动悬起的砂未发生喷射沉积, 即会被转向后的流体“ 清扫” 到原迎流面(离岸方向)沉积, 形成大型反向交错层理(Dumas and Arnott, 2006)。

在与浅化波同向叠加的反向复合流中, 由于该阶段中单向流与振荡流方向相反, 且振荡流速度小, 再加上单向流在垂向上的抑制作用, 不形成涡流(图 4-2c, 也可参照图 3-3c), 又由于前一阶段大量悬浮砂粒在波谷降落沉积, 故可形成弱不对称的底床形态和厚度向波谷变厚的纹层(Dumas et al., 2005)。在接下来的沉积阶段, 其沉积则为背流面崩落沉积(S4), 故可形成单向交错层理, 当上一阶段的崩落沉积保存下来时, 也可发育双向交错层理, 与上一沉积阶段形成的浪成波纹层理一起可组成不能充分发育且频繁交替的复杂沉积构造(Meene et al., 1996)。在与对称波和浅化波同相叠加的情况下, 由于单向流对振荡流的抑制和在振荡流反向时对波峰的“ 清扫” , 一般均可形成波峰圆滑、弱显不对称的形态(Dumas et al., 2005; Perillo et al., 2014a)。在与浅化波异向叠加的反向复合流中, 尽管底床上的速度(剪切力)不是很大, 但其持续时间长(图 4-3c), 因此形成较强的涡流(Villard and Osborne, 2002; Christensen et al., 2019), 悬砂量也相对较多。在随后的沉积阶段, 会在背流面形成未到崩落点的喷射沉积(S3), 在迎流面形成越过崩落点的喷射沉积(S1), 又由于沉积时间也较短(图 4-3), 故和上半周期的沉积类似(图 4-3b), 也有可能形成残余涡动沉积(S2), 参照近底床流动特征与底床形态的关系(Yamaguchi and Sekiguchi, 2010; Perillo et al., 2014b), 最终有可能形成近于对称的底床形态。

图 5 脉动复合流在波状底床上一个波动周期内砂粒运动示意图
左边为向海岸方向; 右边为向海方向; v— 流体速度, 向岸为正, 向海为负; t— 时间; Ⅰ — 剥蚀区域, Ⅱ — 沉积区域; A— 迎流面涡流, B— 波谷残余涡流, C— 波谷涡流; ta— 为起动阶段最大剥蚀时刻, tc— 第2阶段沉积强度最大时刻, tb1— 第1阶段沉积强度最大时刻, tb2— 2个阶段沉积转换时刻。a— 剥蚀阶段; b— 第1沉积阶段; c— 第2沉积阶段; 在沉积阶段(图 3-1b、3-2b和3-3b中): 实线为tb1时刻, 虚线为tb2时刻。图例中: 1— 振荡流方向与强度; 2— 越过崩落点的喷射沉积(S1); 3— 残余涡动沉积(S2); 4— 未到崩落点的喷射沉积(S3); 5— 背流面的崩落沉积(S4); 6— 垂直降落沉积(S5); 7— 强涡流; 8— 弱涡流; 9— 无涡流; 10— 单向流方向与强度Fig.5 Schematics of sand movements on ripple surface during one wave period under pulsating types of flow

2.3.2 脉动复合流

脉动复合流研究程度较低, 在水槽实验中只有少数实验涉及脉动复合流(Perillo et al., 2014a, 2014b)。由于单向流速度大于振荡流速度, 故在1个周期内只发生1次沉积(图 5-1, 5-2, 5-3), 但仍可分为3个阶段, 即1个剥蚀阶段和2个沉积阶段(Lamb et al., 2008): 剥蚀阶段相当于前面的起动阶段; 第1沉积阶段为振荡流转向前后, 此时振荡流速度最小, 相当于前面的沉积阶段; 第2沉积阶段为振荡流反向速度达到最大值前后, 此时叠加速度最小, 相当于前面的反向剥蚀阶段, 会发生单向流的剥蚀与沉积作用(Wu and Parsons, 2019)。

在剥蚀阶段(图 5-1a, 5-2a, 5-3a)与振荡流和反向复合流的起动阶段类似, 在背流面形成涡动, 产生砂云, 随后砂云上升发生沉积。其中与浅化波异向叠加的脉动复合流, 剥蚀阶段在下半周期, 故形成负涡(图 5-3a)。

在第1沉积阶段, 与对称波叠加的脉动复合流(图 5-1b), 由于沉积时间短、振荡流转向快和单向流作用强, 在垂向上流体会迅速地由上升变为下降(Yokokawa et al., 1995), 故以未到崩落点的喷射沉积(S3)为主, 并伴有越过崩落点的喷射沉积(S1); 与浅化波同向叠加的脉动复合流(图 5-2b), 由于沉积时间长、振荡流转向慢和单向流作用强, 故以未到崩落点的喷射沉积(S3)和垂直降落沉积(S5)为主, 并伴有越过崩落点的喷射沉积(S1); 与浅化波异向叠加的脉动复合流, 由于沉积时间短、振荡流转向快和单向流沿砂粒喷射方向叠加, 故以越过崩落点的喷射沉积(S1)为主, 以未到崩落点的喷射沉积(S3)为辅(图 5-3b)。

在第2沉积阶段(图 5-1c, 5-2c, 5-3c), 由于单向流的作用, 会在其背流面形成崩落沉积(S5), 在与对称波和浅化波同向叠加的脉动复合流中, 由于沉积时间较长(图 5-1c, 5-2c), 崩落沉积则有可能保存, 只是不会充分发育(Meene et al., 1996); 在与浅化波异向叠加的脉动复合流中, 由于沉积时间短, 崩落沉积难以保存(图 5-3c)。此外, 在与对称波同向叠加的脉动复合流中, 由于悬砂量较大, 振荡流反向阶段沉积时间较长(图 5-1), 则有可能形成垂直降落沉积(S5)。就底床形态而言, 3种情形均易形成波峰圆滑且不对称的波痕(Perillo et al., 2014a, 2014b); 但就纹层厚度的变化, 与对称波和浅化波同向叠加的脉动复合流, 易形成向波峰变薄、向波谷变厚的纹层。

3 复合流沉积特征分析

根据已有的复合流研究成果和砂粒在复合流中的运动(Yokokawa et al., 1995; Dumas et al., 2005; Perillo et al., 2014a, 2014b), 并结合反向复合流在1个周期内的2次沉积(Davies et al., 1988; Lamb et al., 2008), 可初步概括出复合流所形成的沉积构造特征(表 1)。

表 1 复合流沉积特征分析 Table1 Analysis for sedimentary characteristics of combined flow

在与对称波叠加形成的反向复合流中, 尽管在半周期的沉积过程中形成近于对称的底床形态, 但在同振荡流方向叠加和反振荡流方向叠加的半周期中, 其对底床的剥蚀程度、流体中的悬砂量差别较大, 其沉积距崩落点的位置稍有差异, 故形成圆顶、弱不对称及丘状形态(Arnott and Southard, 1990; Dumas et al., 2005)。在与浅化波传播方向同向叠加形成的反向复合流中, 在同振荡流方向叠加的半周期中, 沉积时间变长, 剥蚀时间变短(图 4-2), 在波谷形成垂直降落沉积(图 4-2b), 在反振荡流方向叠加的半周期中, 悬砂量少, 沉积时间短(图 4-2), 故易形成具有弱不对称且光滑的波峰、上凸或曲线型的纹层, 同时纹层在波峰处变薄、在波谷处变厚, 这是目前总结的典型的复合流层理的特征。在与浅化波传播方向异向叠加形成的反向复合流中, 在同振荡流方向叠加的半周期中, 剥蚀强度大, 但剥蚀时间短, 在反振荡流方向叠加的半周期中, 剥蚀强度较小, 但剥蚀时间长, 同时2个半周期中沉积时间差不多(图 4-3), 故悬砂量、沉积类型和沉积位置都相近, 因而形成圆顶、近对称及丘状形态。这种近于对称的波痕及丘状交错层理在三角洲环境中洪水或风暴回流与风暴作用(与传播方向异向叠加)形成的复合流沉积中已有发现(Collins et al., 2017)。

对于脉动复合流, 在反振荡流方向叠加时, 不再形成涡流剥蚀悬砂(图 5-1c, 5-2c), 因此在1个周期内只出现1次剥蚀和沉积的转换(图 5-1, 5-2, 5-3)。当其与对称波叠加时, 在振荡流反向前, 由于单向流对涡流上升的抑制作用, 形成具有弱不对称的未到崩落点的喷射沉积和越过崩落点的喷射沉积(图 5-1b), 在振荡流反向后, 则会形成垂直降落沉积和背流面崩落沉积(图 5-1c), 故总体上形成典型的复合流层理, 同时可能保存极少量单向流沉积(Lamb et al., 2008; Christensen et al., 2019); 当其与浅化波传播方向同向叠加时, 剥蚀时间短而沉积时间长(图 5-2), 悬浮的颗粒有充足的时间沉积, 前期形成具有弱不对称的未到崩落点的喷射沉积和越过崩落点的喷射沉积, 后期形成垂直降落沉积(图 5-2b), 在沉积阶段即形成典型的复合流层理(Lamb et al., 2008); 当其与浅化波传播方向异向叠加时, 剥蚀时间长而沉积时间短(图 5-3), 悬浮的颗粒没有充足的时间沉积, 在下一剥蚀阶段会继续保持悬浮, 流体中会保持大量的悬浮颗粒(图 5-3c), 故易形成具有爬升特点的复合流层理(Myrow et al., 2002; Lamb et al., 2008)。

当复合流能量增强时, 在细砂中, 反向复合流先形成丘(洼)状交错层理, 脉动复合流先形成大型低角度(小于15° )交错层理, 此后能量进一步增强, 反向复合流和脉动复合流均形成准平行层理和平行层理(Nø ttvedt and Kreisa, 1987; Paz et al., 2019)。这种差别可分析如下: 当反向复合流能量增强时, 其平衡底床形态由对称和不对称小型3D波痕(三维波痕)变为对称和不对称大型波痕, 其波高增加, 在振荡流主控下, 小的复合流波痕通过合并形成较大的圆顶波痕(Doucette and O’ Donoghue, 2006), 当垂向加积速率较高时保存为丘状, 否则为洼状(Dumas and Arnott, 2006; Paz et al., 2019); 而脉动复合流以单向流主控, 其平衡底床形态可由不对称小型3D波痕、大型3D波痕和流水波痕等进入平行层理区(Perillo et al., 2014a, 2014b), 其中在经过大型3D波痕区时, 对细砂、粉砂而言, 由于振荡流分量使进入流体中的颗粒升高, 从而抑制颗粒的崩落沉积, 故形成低角度(Nø ttvedt and Kreisa, 1987)。

当复合流中振荡流的周期增大时, 其剥蚀时间和沉积时间都会相应增加, 有利于未到崩落点的喷射沉积和背流面的崩落沉积(两者为同一侧沉积), 而不利于越过崩落点的喷射沉积、残余涡动沉积和垂直降落沉积, 这和复合流水槽实验中当振荡流周期增大时(如从8 s到10.5 s), 对称波痕区域缩小而不对称波痕区域增大的结果一致(Dumas et al., 2005; Perillo et al., 2014a)。因此在较大周期振荡流形成的复合流中, 较难发育典型的复合流层理, 而会出现明显而频繁的剥蚀面、复合流层理和单向流层理的交替, 同时2种层理均不能充分发展(Wagoner de Meene et al., 1996)。此外, 除与浅化波异向叠加外, 当流体本身为负载流体时, 各种叠加方式形成的复合流均易出现爬升层理特征, 如低密度浊流和洪水形成的复合流(Jobe et al., 2012; Bowman et al., 2014; Collins et al., 2017; Pomar et al., 2019)。

综合反向复合流和脉动复合流的沉积特征, 主要有以下几点和已有研究成果相符: (1)以表 1为基础, 典型复合流层理在反向复合流沉积中占1/3, 在脉动复合流沉积中占2/3, 这和水槽实验的观察结果一致, 即复合流层理在以波动主控的复合流中发育少, 而在以单向流主控的复合流中发育得多(Yokokawa, 1995; Yokokawa et al., 1995); (2)不对称小型丘状交错层理和具有爬升特点的复合流层理已作为复合流的鉴别标志得到广泛的应用(Lamb et al., 2008; Basilici et al., 2012; Collins et al., 2017), 和上述反向复合流和脉动复合流的基本特征一致; (3)在细砂中, 丘状交错层理出现在向平行层理转化的过程中, 和有些学者认为丘状交错层理为非稳定状态下的产物的结论一致(Quin, 2011), 同时也和水槽实验结果一致, 在实验中, 丘状交错层理发育区域不稳定, 但都在反向复合流区并沿平行层理区域下边缘分布(Dumas et al., 2005; Perillo et al., 2014b); (4)在以浊流为单向流分量的复合流中普遍发育具有爬升特点的复合流层理(Myrow et al., 2002; Lamb et al., 2008)。

4 复合流沉积构造鉴别标志

复合流具有和单向流、振荡流及双向交替流不同的沉积机制(李向东, 2020a), 故可在粉砂和细砂中由悬浮砂粒形成特征性的沉积构造, 并可作为地层记录中复合流沉积的鉴别标志(Arnott, 1993; Myrow et al., 2002; Hill et al., 2003; Lamb et al., 2008; Harazim and Mcilroy, 2015)。依据水槽实验和沉积实例研究的成果, 目前总结出的复合流沉积构造鉴别标志主要有: 复合流波痕、复合流层理、爬升型复合流层理、不对称丘状交错层理、准平行层理和不能充分发育的浪成波纹层理与流水层理的频繁交替(图 6)。

复合流波痕是最早观察到的复合流沉积特征(Harms, 1969), 至今仍然是鉴别复合流沉积的最重要和最常用的标志之一。在形态上, 复合流波痕具有不对称且光滑的波峰(图 6-a), 可出现2D波痕向3D波痕的转化及波痕分叉现象(龚一鸣等, 2003; 李向东等, 2010)。在统计特征上, 主要有以下4点(Banerjee, 1996): (1) 波痕指数和不对称指数介于流水波痕和浪成波痕之间, 表现出过渡性质, 其不对称程度小于浅化波波痕(Yamaguchi and Sekiguchi, 2010); (2) 相同环境下形成的波痕, 其波长在统计上满足对数正态分布规律; (3)不同环境下形成的波痕, 其波长会随着波动的浅化而变长, 或因波动的周期性变化(如气候驱动的海平面升降或米兰柯维奇旋回)而出现有规律的增减; (4)波长、波高在对数图解上, 除波高小于1.3 cm的2D波痕外, 呈现线性变化趋势。

图 6 典型的复合流沉积构造
a— 复合流波痕(Basilici et al., 2012); b— 复合流层理(李向东等, 2010); c— 爬升型复合流层理(Lamb et al., 2008); d— 不对称丘状交错层理(McKie, 1994); e— 准平行层理(Arnott, 1993); f— 近水平或不规则侵蚀面(红线)和频繁交替出现的浪成波纹层理和流水层理, 且两者发育均不充分, 其中T为潮汐成因构造, W为波浪成因构造, f1至f7为沉积构造自下而上可分为7组(Meene et al., 1996)Fig.6 Representative sedimentary structures of combined-flow

复合流层理是复合流波痕在层内的表现, 具有复合流波痕不对称且光滑的波峰(图 6-b, 6-c)。典型的复合流层理纹层呈上凸或曲线型, 同时在波峰处变薄, 在波谷处变厚(图 6-b)。爬升层理为沉积物负载流体所形成, 爬升沙丘交错层理已见报道(Ghienne et al., 2010), 浊流沉积中的爬升层理则更为普遍(Jobe et al., 2012)。爬升型复合流层理兼具有爬升层理和复合流层理的特点, 但纹层上凸, 纹层向下往往渐变为近水平的形态(图 6-c), 多出现在与低密度浊流有关的高悬浮复合流沉积中(Myrow et al., 2002; Lamb et al., 2008; 李向东等, 2010)。复合流层理是目前应用最为广泛的复合流沉积鉴别标志(Myrow and Southard, 1991; Hill et al., 2003; Harazim and Mcilroy, 2015)。

丘状交错层理的成因一直争议很大(项立辉等, 2007; 李向东, 2020b), 但随着流体沉积机制研究的深入, 丘状交错层理除了纯振荡流形成机制外, 即强的纯振荡衰减流可在平的底床上形成大型丘状交错层理(Southard et al., 1990; 赖志云和赖庆伟, 2010), 其主要的形成机制为复合流的参与沉积, 具体可细分为3类: (1)振荡流本身会产生相应的单向流与之叠加, 主要包括衰减期风暴产生的振荡流与底摩擦主控回流形成的复合流产生丘状交错层理(McKie, 1994)和内波形成的丘状交错层理(Morsilli and Pomar, 2012); (2)叠加的振荡流和单向流均为牵引流, 主要包括风暴产生的原生振荡流和次生沿岸流形成的复合流产生丘状交错层理(Greenwood, 1986)及风暴产生的振荡流与地转流形成的复合流产生丘状交错层理(Midtgaard, 1996); (3)密度流与重力波产生的不稳定流体形成丘状交错层理(Quin, 2011), 主要包括浊流与驻波形成的复合流产生丘状交错层理(Prave and Duke, 1990; Mulder et al., 2009; 师庆民等, 2013)及低密度浊流与短周期内波产生的复合流形成的丘状交错层理(李向东等, 2010、2019; Tinterri et al., 2016), 此外与异重流相关的丘状交错层理也可归为此类(Basilici et al., 2012)。从宏观上讲, 丘状交错层理的形成多和风暴有关(项立辉等, 2007; 钟建华等, 2016; Paz et al., 2019), 其次为内波、浊流和异重流等(Mulder et al., 2009; Morsilli and Pomar, 2012; Pomar et al., 2019), 同时在长周期波动产生的双向流中也有发现(Greenwood, 1986); 从微观上讲则多和复合流相关, 其次才为纯振荡流。由于丘状交错层理的不对称性对单向流分量的作用非常敏感(Arnott and Southard, 1990; Dumas and Arnott, 2006), 故不对称丘状交错层理(图 6-d)可作为复合流存在的证据(Lamb et al., 2008; Morsilli and Pomar, 2012), 但若用于叠加的振荡流和单向流类型, 则需要根据沉积特征、沉积环境和古水流方向等做出具体分析。

准平行层理是指纹层显示出模糊但可辨的波状起伏的一种层理, 波长与波高之比一般大于100(Arnott and Southard, 1990; Arnott, 1993)。复合流形成的准平行层理序列可分为底部起伏的剥蚀面、中部准平行层理、上部小型的复合流波痕3个部分(图 6-e), 前人认为这是在高流态复合流条件下(Arnott, 1993; Lamb et al., 2008), 强振荡流与由弱变强的单向流复合而成的衰弱流沉积而成的(Arnott, 1993)。准平行层理介于丘状交错层理与平行层理之间, Arnott(1993)认为在开始阶段, 强振荡流主控的复合流可形成丘状交错层理, 但随着单向流分量的增强, 丘状交错层理被剥蚀, 而最终保存了准平行层理。李向东等(2010)在宁夏香山群徐家圈组深水钙质粉砂岩中发现准平行层理与小型不对称丘状交错层相互叠置, 两者之间存在明显的剥蚀面, 可作为此种观点的一个证据。

复合流沉积源于水槽实验, 此后才在地层记录中识别出来。在水槽实验中, 水动力条件都比较简单, 一般为正弦波与单向流的同向或异向叠加, 因此均得到典型的复合流沉积构造, 而在地层记录中主要是识别在水槽实验中得到的典型沉积构造, 用以鉴别复合流沉积的存在。但是在现代沉积物的研究中出现了复杂的沉积构造, Meene等(1996)在研究现代浅海复杂单向流(潮汐流、风驱沿岸流和风暴回流)条件下的复合流沉积时认为, 不规则低角度侵蚀面、浪成波纹层理和单向流沉积构造的频繁交替出现, 且均不能充分发育, 可作为复合流沉积的鉴别特征(图 6-f)。在图 6-f中, 沉积构造从下到上可分为7组(f1至f7): 在f1中, 从右向左为纹层倾角连续变化的浪成波纹层理转变为潮汐成因具有低角度层系界面的交错层理(砂粒降落形成); 在f2中, 从左向右依次为低角度交错层理(可能代表丘状交错层理)、潮汐束(T)和纹层倾角连续变化的浪成波纹层理(W); 在f3中, 从右向左, 水平或低角度浪成波纹层理侧向上变为不规则削截; 在f4、f5中多发育浪成波纹层理(W); 在f6、f7中多发育潮汐成因构造(T), 其中仅在f7中出现高起伏的波浪剥蚀面(W)。此外, 在地层记录中还发现了单向流交错层理顶部覆盖有对称的纹层, 作者解释为复合流成因(Plint et al., 2012), 也可作为复合流沉积中单向流沉积构造与振荡流沉积构造交替出现的证据。

5 结论

1)波— 流相互作用形成的复合流可分为正压反向复合流、斜压反向复合流、正压脉动复合流和斜压脉动复合流4类, 在每一类中可再以波动类型和波、流叠加方式进行细分。

2)复合流总体上属于衰弱流悬浮沉积。其微观的沉积机制可分为5种: 越过崩落点的喷射沉积(S1), 残余涡动沉积(S2), 未到崩落点的喷射沉积(S3), 背流面的崩落沉积(S4), 垂直降落沉积(S5)。其沉积过程总体上受悬砂量和沉积时间的控制, 可进一步细分为: 振荡流分量的周期、强度、对称性和转向快慢; 单向流分量强度和叠加方向; 颗粒剥蚀和沉积时间的长短及其比例关系。

3)目前总结出的可靠的复合流沉积构造(悬浮沉积机制)鉴别标志主要有: 复合流波痕、复合流层理、爬升型复合流层理、不对称丘状交错层理、准平行层理和不能充分发育的浪成波纹层理与流水层理的频繁交替等6类。

(责任编辑 张西娟; 英文审校 刘贺娟)

参考文献
[1] 方欣华, 杜涛. 2004. 海洋内波基础和中国海内波. 山东青岛: 中国海洋大学出版社, 16-52.
[Fang X H, Du T. 2004. Foundamentals of Oceanic Internal Waves and Internal Waves in the China Seas. Shand ong Qingdao: China Ocean University Press, 16-52] [文内引用:1]
[2] 龚一鸣, 徐冉, 李保华. 2003. 分叉波痕在广西上泥盆统钙质浊积岩中的发现及意义. 地质论评, 19(1): 379-382.
[Gong Y M, Xu R, Li B H. 2003. Ripple marks with bifurcation from the calcareous turbidite sequence of the Upper Devonian in Guangxi, South China. Geological Review, 19(1): 379-382] [文内引用:1]
[3] 赖志云, 赖庆伟. 2010. 丘状交错层理的成因探讨. 石油天然气学报(江汉石油学院学报), 32(5): 42-45.
[Lai Z Y, Lai Q W. 2010. Study on the genesis of moundy cross-stratification. Journal of Oil and Gas Technology, 32(5): 42-45] [文内引用:1]
[4] 李向东. 2013. 关于深水环境下内波、内潮汐沉积分类的探讨. 地质论评, 59(6): 1097-1109.
[Li X D. 2013. Proposed classification of internal-wave and internal-tide deposits in deep-water environment. Geological Review, 59(6): 1097-1109] [文内引用:1]
[5] 李向东. 2020 a. 浅议沉积学中的流体问题. 世界地质, 39(1): 45-55.
[Li X D. 2020 a. An overview of hydromechanics in sedi mentology. Global Geology, 39(1): 45-55] [文内引用:5]
[6] 李向东. 2020 b. 丘状和似丘状交错层理成因机制研究进展. 古地理学报, 22(6): 1065-1080.
[Li X D. 2020 b. Advances in genetic mechanism research on hummocky and hummocky-like cross-stratifications. Journal of Palaeogeography(Chinese Edition), 22(6): 1065-1080] [文内引用:2]
[7] 李向东, 何幼斌, 郑昭昌, 刘娜, 王丹, 罗进雄, 李华. 2010. 宁夏香山群徐家圈组发现深水复合流沉积构造. 地质学报, 84(2): 221-232.
[Li X D, He Y B, Zheng Z C, Liu N, Wang D, Luo J X, Li H. 2010. Deep-water combined-flow sedimentary structures in Xujiajuan Formation of Xiangshan Group, Ningxia. Acta Geologica Sinica, 84(2): 221-232] [文内引用:6]
[8] 李向东, 陈海燕, 陈洪达. 2019. 鄂尔多斯盆地西缘桌子山地区上奥陶统拉什仲组深水复合流沉积. 地球科学进展, 34(12): 1301-1305.
[Li X D, Chen H Y, Chen H D. 2019. Deep-water combined-flow deposits of the upper Ordovician Lashenzhong Formation in Zhuozishan area, western margin of Ordos Basin. Advances in Earth Science, 34(12): 1301-1305] [文内引用:2]
[9] 林缅, 袁志达. 2005. 振荡流作用下波状底床上流场特性的实验研究. 地球物理学报, 48(6): 1466-1474.
[Lin M, Yuan Z D. 2005. Investigation of characteristics of fluid field over wavy beds under oscillatory flow. Chinese Journal of Geophysics, 48(6): 1466-1474] [文内引用:6]
[10] 师庆民, 冯乐, 窦鲁星, 刘绍莉, 江煜波, 孙晓倩. 2013. 基于驻波理论解释丘状交错层理: 以徐州地区贾园组风暴沉积为例. 沉积学报, 31(6): 1008-1013.
[Shi Q M, Feng L, Dou L X, Liu S L, Jiang Y B, Sun X Q. 2013. Explaining hummocky cross-stratification based on the theory of stand ing wave: a case from Jiayuan Group storm deposits in Xuzhou. Acta Sedimentologica Sinica, 31(6): 1008-1013] [文内引用:2]
[11] 王家豪, 王华, 曾劲彪, 程海. 2017. 山东省中部上寒武统碳酸盐风暴沉积的综合模式. 地球科学, 42(1): 68-77.
[Wang J H, Wang H, Zeng J B, Cheng H. 2017. Integrative depositional model for carbonate tempestites in Upper Cambrian, central Shand ong Province. Earth Science, 42(1): 68-77] [文内引用:1]
[12] 王涛, 李家春. 1999. 波流相互作用研究进展. 力学进展, 29(3): 331-343.
[Wang T, Li J C. 1999. On wave-current interaction. Advances in Mechanics, 29(3): 331-343] [文内引用:3]
[13] 项立辉, 刘健, 曹志敏. 2007. 丘状交错层理研究述评. 海洋地质动态, 23(8): 19-24.
[Xiang L H, Liu J, Cao Z M. 2007. Review of hummocky cross-stratification research. Marine Geology Letter, 23(8): 19-24] [文内引用:2]
[14] 许安涛, 李凤杰, 刘奎, 向鹏飞, 赵晨圆, 胡鹏. 2018. 北川甘溪下泥盆统风暴岩沉积特征及其沉积模式. 中国地质, 45(5): 1049-1062.
[Xu A T, Li F J, Liu K, Xiang P F, Zhao C Y, Hu P. 2018. The characteristics and sedimentary model of storm deposits in the Lower Devonian strata of Beichuan. Geology in China, 45(5): 1049-1062] [文内引用:1]
[15] 徐祥德, 冉令坤. 2007. 波流相互作用与波动传播模态. 大气科学, 31(6): 1237-1250.
[Xu X D, Ran L K. 2007. Wave-flow interaction and wave-propagation modes. Chinese Journal of Atmospheric Sciences, 31(6): 1237-1250] [文内引用:1]
[16] 张昊, 李凤杰, 沈凡, 陈政安, 倪子尧. 2019. 四川盆地龙门山区甘溪石沟里泥盆系养马坝组风暴沉积特征及其地质意义. 古地理学报, 21(3): 441-450.
[Zhang H, Li F J, Shen F, Chen Z A, Ni Z Y. 2019. Storm deposits characteristics and its geological significance in the Devonian Yangmaba Formation from Shigouli section, Longmenshan area, Sichuan Basin. Journal of Palaeogeography(Chinese Edition), 21(3): 441-450] [文内引用:1]
[17] 钟建华, 倪良田, 邵珠福, 李勇, 刘选, 毛毳, 刘圣鑫, 孙宁亮, 陈彬, 王凯, 罗可, 王韶洁, 刘闯, 刘宝, 熊志强. 2016. 青岛灵山岛下白垩统风暴岩与风暴沉积的发现及意义. 古地理学报, 18(3): 381-398.
[Zhong J H, Ni L T, Shao Z F, Li Y, Liu X, Mao C, Liu S X, Sun N L, Chen B, Wang K, Luo K, Wang S J, Liu C, Liu B, Xiong Z Q. 2016. Tempestites and storm deposits in the Lower Cretaceous from Lingshan Island , Qingdao. Journal of Palaeogeography(Chinese Edition), 18(3): 381-398] [文内引用:2]
[18] Arnott R W C. 1993. Quasi-planar-laminated sand stone beds of the Lower Cretaceous Bootlegger Member, north-central Montana: evidence of combined-flow sedimentation. Journal of Sedimentary Research, 63(3): 488-494. [文内引用:5]
[19] Arnott R W, Southard J B. 1990. Exploratory flow-duct experiments on combined-flow bed configurations and some implications for interpreting storm-event stratification. Journal of Sedimentary Petrology, 60(2): 211-219. [文内引用:4]
[20] Basilici G, de Luca P H V, Poiré D G. 2012. Hummocky cross-stratification-like structures and combined-flow ripples in the Punta Negra Formation(Lower-Middle Devonian, Argentine Precordillera): a turbiditic deep-water or storm-dominated prodelta inner-shelf system? Sedimentary Geology, 267-268: 73-92. [文内引用:3]
[21] Banerjee I. 1996. Population, trand s, and cycles in combined-flow bedforms. Journal of Sedimentary Research, 66(5): 868-874. [文内引用:1]
[22] Bowman A P, Howard D, Johnson H D. 2014. Storm-dominated shelf-edge delta successions in a high accommodation setting: the palaeo-Orinoco Delta(Mayaro Formation), Columbus Basin, South-East Trinidad. Sedimentology, 61(3): 792-835. [文内引用:2]
[23] Christensen D F, Brinkkemper J, Ruessink G, Aagaard T. 2019. Field observations of intra-wave sediment suspension and transport in the intertidal and shallow subtidal zones. Marine Geology, 413: 10-26. [文内引用:4]
[24] Collins D S, Johnson H D, Allison P A, Guilpain P, Damit A R. 2017. Coupled ‘storm-flood’ depositional model: application to the Miocene-Modern Baram Delta Province, north-west Borneo. Sedimentology, 64(5): 1203-1235. [文内引用:4]
[25] Davies A G, Soulsby R L, King H L. 1988. A numerical model of the combined wave and current bottom boundary layer. Journal of Geophysical Research, 93(C1): 491-508. [文内引用:10]
[26] Doucette J S, O’Donoghue T. 2006. Response of sand ripples to change in oscillatory flow. Sedimentology, 53(3): 581-596. [文内引用:1]
[27] Dumas S, Arnott R W C, Southard J B. 2005. Experiments on oscillatory-flow and combined-flow bed forms: implications for interpreting parts of the shallow-marine sedimentary record. Journal of Sedimentary Research, 75(3): 501-513. [文内引用:13]
[28] Dumas S, Arnott R W C. 2006. Origin of hummocky and swaley cross-stratification: The controlling influence of unidirectional current strength and aggradation rate. Geology, 34(12): 1073-1076. [文内引用:5]
[29] Felletti F, Dall’olio E, Muttoni G. 2016. Determining flow directions in turbidites: an integrated sedimentological and magnetic fabric study of the Miocene Marnoso Arenacea Formation(northern Apennines, Ita ly). Sedimentary Geology, 335: 197-215. [文内引用:1]
[30] Harazim D, Mcilroy D. 2015. Mud-rich density-driven flows along an early Ordovician storm-dominated shoreline: implications for shallow-marine facies models. Journal of Sedimentary Research, 85(5): 509-528. [文内引用:3]
[31] Harms J C. 1969. Hydraulic significance of some sand ripples. Geological Society of America Bulletin, 80(3): 363-396. [文内引用:2]
[32] Hill P R, Meulé S, Longuépée H. 2003. Combined-flow processes and sedimentary structures on the shoreface of the wave-dominated grand e-riviére-de-la-baleine delta. Journal of Sedimentary Research, 73(2): 217-226. [文内引用:4]
[33] Ghienne J F, Girard F, Moreau J, Rubino J I. 2010. Late Ordovician climbing-dune cross-stratification: a signature of outburst floods in proglacial outwash environments? Sedimentology, 57(5): 1175-1198. [文内引用:1]
[34] Greenwood B. 1986. Hummocky cross-stratification in the surf zone: flow parameters and bedding genesis. Sedimentology, 33(1): 33-45. [文内引用:3]
[35] Jobe Z R, Lowe D R, Morris W R. 2012. Climbing-ripple successions in turbidite systems: depositional environments, sedimentation rates and accumulation times. Sedimentology, 59(3): 867-898. [文内引用:2]
[36] Lamb M P, Myrow P M, Lukens C, Houck K, Strauss J. 2008. Deposits from wave-influenced turbidity currents: Pennsylvanian Minturn Formation, Colorado, USA. Journal of Sedimentary Research, 78(7): 480-498. [文内引用:15]
[37] Li M Z, Amos C L. 1999. Sheet flow and large wave ripples under combined wave and currents: field observations, model predictions and effects on boundary layer dynamics. Continental Shelf Research, 19(5): 637-663. [文内引用:2]
[38] Li M, O’Connor B A. 2007. Numerical study of sediment transport above rippled beds under the action of combined waves and currents. Sedimentology, 54(6): 1345-1363. [文内引用:5]
[39] Lu J, Wang X H, Babanin A V, Aijaz S, Qiao F. 2017. Modeling of suspended sediment concentrations under combined wave-current flow over rippled bed. Estuarine, Coastal and Shelf Science, 199: 59-73. [文内引用:2]
[40] McKie T. 1994. Geostrophic versus friction-dominated storm flow: palaeo current evidence from the Late Permian Brotherton Formation, England . Sedimentary Geology, 93(1-2): 73-84. [文内引用:1]
[41] Meene J W H, Boersma J R, Terwindt J H J. 1996. Sedimentary structures of combined flow deposits from the shoreface-connected ridges along the central Dutch coast. Marine Geology, 131(3-4): 151-175. [文内引用:3]
[42] Midtgaard H. 1996. Inner-shelf to lower-shoreface hummocky sand stone bodies with evidence for geostrophic influenced combined flow, Lower Cretaceous, West Greenland . Journal of Sedimentary Research, 66(2): 343-353. [文内引用:1]
[43] Molgat M, Arnott R W C. 2001. Combined tide and wave influence on sedimentation patterns in the Upper Jurassic Swift Formation, south-eastern Alberta. Sedimentology, 48(6): 1353-1369. [文内引用:1]
[44] Morsilli M, Pomar L. 2012. Internal waves vs. surface storm waves: a review on the origin of hummocky cross-stratification. Terra Nova, 24(4): 273-282. [文内引用:3]
[45] Mulder T, Razin P, Faugeres J C. 2009. Hummocky cross-stratification-like structures in deep-sea turbidites: Upper Cretaceous Basque basins(Western Pyrenees, France). Sedimentology, 56(4): 997-1015. [文内引用:1]
[46] Myrow P M, Southard J B. 1991. Combined-flow model for vertical stratification sequences in shallow marine storm-deposited beds. Journal of Sedimentary Petrology, 61(2): 202-210. [文内引用:1]
[47] Myrow P M, Fischer W, Goodge J W. 2002. Wave-modified turbidites: combined-flow shoreline and shelf deposits, Cambrian, Antarctica. Journal of Sedimentary Research, 72(5): 641-656. [文内引用:5]
[48] Nøttvedt A, Kreisa R D. 1987. Model for the combined-flow origin of hummocky cross-stratification. Geology, 15(4): 357-361. [文内引用:3]
[49] Patacci M, Haughton P D W, Mccaffrey W D. 2014. Rheological com plexity in sediment gravity flows forced to decelerate against a confining slope, Braux, SE France. Journal of Sedimentary Research, 84(4): 270-277. [文内引用:2]
[50] Paz M, Ponce J J, Buatois L A, Móngano M G, Carmona N B, Pereira E, Desjardins P R. 2019. Bottomset and foreset sedimentary processes in the mixed carbonate-siliciclastic Upper Jurassic-Lower Cretaceous Vaca Muerta Formation, Picún Leufú Area, Argentina. Sedimentary Geology, 389: 161-185. [文内引用:4]
[51] Perillo M M, Best J L, Garcia M H. 2014 a. A new phase diagram for combined-flow bedforms. Journal of Sedimentary Research, 84(4): 301-313. [文内引用:11]
[52] Perillo M M, Best J L, Yokokawa M, Sekiguchi T, Takagawa T, Garcia M H. 2014 b. A unified model for bedform development and equilibrium under unidirectional, oscillatory and combined-flows. Sedimentology, 61(7): 2063-2085. [文内引用:10]
[53] Plint A G, Macquaker J H S, Varban B L. 2012. Bedload transport of mud across a wide, storm-influenced ramp: Cenomanian-Turonian Kaskapau Formation, Western Canada foreland basin. Journal of Sedimentary Research, 82(11): 801-822. [文内引用:2]
[54] Prave A R, Duke W L. 1990. Small-scale hummocky cross-stratification in turbidites: a form of antidune stratification? Sedimentology, 37(3): 531-539. [文内引用:2]
[55] Pomar L, Molina J M, Ruiz-Ortiz P A, Vera J A. 2019. Storms in the deep: tempestite- and beach-like deposits in pelagic sequences(Jurassic, Subbetic, South of Spain). Marine and Petroleum Geology, 107: 365-381. [文内引用:3]
[56] Quin J M. 2011. Is most hummocky cross-stratification formed by large-scale ripples? Sedimentology, 58(6): 1414-1433. [文内引用:2]
[57] Raaf de J F M, Boersma J R, Gelder V A. 1977. Wave-generated structures and sequences from a shallow marine succession, Lower Carboniferous, County Cork, Ireland . Sedimentology, 24(4): 451-483. [文内引用:1]
[58] Raushan P K, Singh S K, Debnath K, Mukherjee M, Mazumder B S. 2018. Distribution of turbulent energy in combined wave current flow. Ocean Engineering, 167: 310-316. [文内引用:3]
[59] Ribberink J S, Werf J J, O’Donoghue T. 2007. Sand motion induced by oscillatory flows: Sheet flow and vortex ripples. In: Geurts B J et al(eds). Particle Laden Flow: From Geophysical to Kolmogorov Scales. Springer, 3-14. [文内引用:3]
[60] Ruessink B G, Michallet H, Abreu T, Sancho F, van der A D A, van der Werf J J, Silva P A. 2011. Observations of velocities, sand concentrations, and fluxes under velocity-asymmetric oscillatory flows. Journal of Geophysical Research, 116: C03004. [文内引用:1]
[61] Singh S K, Debnath K. 2016. Combined effects of wave and current in free surface turbulent flow. Ocean Engineering, 127: 170-189. [文内引用:2]
[62] Southard J B, Lambie J M, Federico D C, Pile H T, Weidman C R. 1990. Experiments on bed configurations in fine sand s under bidirectional purely oscillatory flow, and the origin of hummocky cross-stratification. Journal of Sedimentary Petrology, 60(1): 1-17. [文内引用:1]
[63] Tinterri R, Magalhaes P M, Tagliaferri A, Cunha R S. 2016. Convolute laminations and load structures in turbidites as indicators of flow reflections and decelerations against bounding slopes: examples from the Marnoso-arenacea Formation(northern Italy)and Annot Sand stones(south eastern France). Sedimentary Geology, 344: 382-407. [文内引用:3]
[64] Villard P V, Osborne P D. 2002. Visualization of wave-induced suspension patterns over two-dimensional bedforms. Sedimentology, 49(2): 363-378. [文内引用:3]
[65] Wagoner de Meene J W H, Boersma J R, Terwindt J H J. 1996. Sedimentary structures of combined flow deposits from the shoreface-connected ridges along the central Dutch coast. Marine Geology, 131(3-4): 151-175. [文内引用:1]
[66] Wu X, Parsons D R. 2019. Field investigation of bedform morphodynamics under combined flow. Geomorphology, 339: 19-30. [文内引用:7]
[67] Yamaguchi N, Sekiguchi H. 2010. Effects of settling and preferential deposi tion of sediment on ripple roundness under shoaling waves. Journal of Sedimentary Research, 80(9): 781-790. [文内引用:14]
[68] Yokokawa M. 1995. Combined-flow ripples: genetic experiments and applications for geologic records. In: Memoirs from the Faculty of Science: Kyushu University, Series D. Earthand Planetary Sciences, Fukuoka, Japan, 29(1): 38. [文内引用:11]
[69] Yokokawa M, Masuda F, Endo N. 1995. Sand particle movement on migrating combined-flow ripples. Journal of Sedimentary Research, A65(1): 40-44. [文内引用:1]
[70] Zedler E A, Street R L. 2006. Sediment transport over ripples in oscillatory flow. Journal of Hydraulic Engineering, 132(2): 180-193. [文内引用:4]
[71] Zhang C, Zheng J H, Wang Y G, Demirbilek Z. 2011. Modeling wave-current bottom boundary layers beneath shoaling and breaking waves. Geo-Marine Letters, 31(1): 189-201. [文内引用:2]