引用本文
于兴河, 李顺利, 孙洪伟. (2022)碎屑岩沉积从源到汇的“物-坡”耦合效应* [J]. 古地理学报, 24(6): 1037-1057.
YU Xinghe, LI Shunli, SUN Hongwei. (2022)Coupling effect of “mass-slope”from source to sink in clastic rock deposition[J]. Journal Of Palaeogeography, 24(6): 1037-1057.  
doi: 10.7605/gdlxb.2022.06.075
Permissions
Copyright@2022, 《古地理学报》编辑部
版权所有.《古地理学报》编辑部
碎屑岩沉积从源到汇的“物-坡”耦合效应*
于兴河, 李顺利, 孙洪伟
中国地质大学(北京)能源学院,北京 100083

第一作者简介 于兴河,男,1958年生,教授,博士生导师,研究方向为储层沉积学与含油气盆地分析、油气储层表征与建模技术、海洋油气成藏条件分析及资源评价。E-mail: billyu@cugb.edu.cn。

收稿日期: 2022-08-31 修回日期: 2022-09-26
基金资助: *国家自然科学基金项目(编号: 42272124, 41472091)与国家“十三五”科技重大专项(编号: 2017ZX05001-002)联合资助
摘要

碎屑岩沉积体系的三维展布特征及其成因机制是建立沉积模式与预测其砂体分布的关键,更是沉积学研究的关键性科学问题。国内外绝大多数学者认为其平面形态和剖面充填型式均与其沉积的地形坡度、粒度粗细有密切的联系,但其定量关系并不清楚。建立不同类型沉积体中粒度和坡度之间的定量关系,对于预测沉积体中不同颗粒的运动方式及其分布至关重要。应用“源-汇”系统研究的思路,分析了供源区、搬运(输送)区及汇积区各自的地质特点,从单向水流对不同质量颗粒在静止/运动中的受力分析与沉积前总体地形斜坡设定2个角度,系统分析、推导并模拟了不同碎屑颗粒在纵向剖面上的运动轨迹,其表现为随着设定的坡型呈抛物线变化,反映出沉积物输送营力的变换及其随坡度变化的响应特征。建立了陆相碎屑岩沉积体系纵向剖面的流速与坡度的计算方程,明确指出沉积物的流速或流态决定其沉积方式,阐述了汇积区碎屑颗粒的加积型式与沉积物分布上的总体规律,由此提出碎屑岩沉积体系的“物-坡”耦合效应及其主要内涵,并从多个维度与源-汇的各区段,阐述了“物-坡”耦合效应在各种沉积体系的沉积物类型及其空间形态特征上的地质响应。

关键词: 粒度分布; 地形坡降; 沉积物输送营力; 加积型式; “物-坡”耦合效应
中图分类号:P512.2 文献标志码:A 文章编号:1671-1505(2022)06-1037-21
Coupling effect of “mass-slope”from source to sink in clastic rock deposition
YU Xinghe, LI Shunli, SUN Hongwei
School of Energy Resources, China University of Geosciences(Beijing),Beijing 100083,China

About the first author YU Xinghe,born in 1958,is a professor and supervisor of Ph.D. candidate. He is mainly engaged in reservoir sedimentology and analysis of petroliferous basins,hydrocarbon reservoir characterization and modeling techniques,analysis of marine hydrocarbon accumulation conditions and resource evaluation. E-mail: billyu@cugb.edu.cn.

Fund:Co-funded by the National Natural Science Foundation of China(Nos. 42272124, 41472091)and National Science and Technology Major Project for the 13th Five Year Plan(No.2017ZX05001-002)
Abstract

The three-dimensional spreading characteristics of clastic rock deposition and their genesis mechanisms are the key to establish the depositional models and predict sand distribution,which is a key scientific problem in sedimentology research. Most domestic and abroad scholars considered that the planar geometry and profile filling pattern were closely related to the slope gradient,and grain-size of their deposits. Their quantitative relationships have not been uniformly and clearly understood so far. However,establishing quantitative relationships between grain-size and slope in different types of depositional systems is essential for predicting the movement patterns and their distribution of different particles in sediment bodies. In this paper,the geological characteristics of the source,transport and sink areas were analyzed. Based on the force analysis of unidirectional water flow on different masses of particles at rest / in motion and the general topographic slope setting before deposition, the trajectories of different clastic particles in the longitudinal profile were systematically analyzed,deduced,and simulated,which shows a parabolic change with the set slope shape,reflecting the transformation of sediment-routing agent and its response characteristics with the change of slopes. The quantitative equations of flow velocity and slope of the longitudinal profile of the terrestrial clastic depositional systems were established. It is clearly pointed out that the flow velocity or regime of sediments defines their depositional mode, and general rule of the accretion pattern and sediment distribution in the sink area is clarified. In this paper,the “mass-slope”coupling effect of clastic depositional systems and its main connotation are proposed,and the geological response of the “mass-slope”coupling effect on the distribution of sediment types and their spatial morphological characteristics of various depositional systems is described from various dimensions and source-to-sink segments.

Keyword: grain-size distribution; slope gradient; sediment-routing agent; accreting pattern; “mass-slope”coupling effect
1 概述

陆源碎屑岩沉积体系中砂体的平面展布与垂向上厚薄交互演变的成因机制, 不仅是碎屑岩沉积学的重要科学问题之一, 同时也是油气地质学界与矿产行业长期以来一直关注的重点内容(叶连俊等, 1988; 孙龙德等, 2010; 朱筱敏等, 2016; 于兴河等, 2018), 这是因为其成因的揭示直接影响着不同沉积物分布规律的预测。因此, 建立陆源碎屑沉积体中粒度和坡度之间的定量关系, 对预测沉积体中不同颗粒的运动方式及其分布至关重要。这需要明确控制其沉积过程的内部与外部因素, 尤其是汇积区与地形坡度变化(坡降)对沉积物输送体系的控制机理(徐长贵等, 2017; 王成善和林畅松, 2021; 龚承林等, 2022)。如何预测沉积体系各相带中砂体的空间分布, 或者说要明确控制碎屑岩沉积体系中不同类型沉积物分布上的核心因素?传统的认识是: 不同搬运方式与沉积作用下, 砂体的垂向序列、剖面充填结构与N/G(含砂率)(粒径大于4φ碎屑颗粒含量占总沉积体的比值)变化, 以及平面分布特征明显不同(Reading and Richards, 1994)。近半个多世纪以来, 关于沉积体宏观展布规律、尤其是砂体分布预测的研究着重在3个方面: 沉积体系的成因(Anderton, 1985; Reading, 2009)、层序地层学(Catuneanu, 2006; Catuneanu et al., 2009)以及近年来的“源-汇”系统(Allen, 2008; Sømme and Jackson, 2013; 邵龙义等, 2019), 三者之间既相互联系又各有侧重与补充。然而, 从沉积体系的命名来看, 沉积学自形成以来绝大多数都是从形态特征出发, 以沉积成因为核心来命名(Bull, 1977; Kenyon and Turcotte, 1985; Church, 2006); 而层序地层学则是从各沉积发育在盆地斜坡或地层格架中的位置进行定名(Emery and Myers, 2009; Catuneanu, 2022), 更关注其形成的地形地貌; 如低位扇或斜坡扇, 是三角洲还是水下扇或浊积扇?这就要看其形成的地质背景与沉积成因, 尤其是扇体的垂向沉积成因序列, 才能明确其成因机制与砂体展布的基本特征(于兴河等, 1994, 2018); 从层序地层的角度来看, 明确盆地的斜坡区发育有扇体, 是砂体的主要分布区域, 或者说低位体系域多发育扇体, 有助于厘清层序格架的叠加样式或剖面充填结构, 就已达到了其主要研究目的。但对预测该沉积体系中砂体的分布而言, 则需要进一步明确沉积体的成因、N/G的大小及其空间展布的特征(Shanmugam, 2013; 于兴河等, 2013; Allen, 2017)。这就是说层序地层学的四大因素(构造、物源、基准面(海/湖平面)及气候变化)是控制沉积体系的必要条件(Catuneanu et al., 2009), 而沉积成因则是其充分条件。由此说明层序地层的四要素并非沉积学对应的控制因素(Hoy and Ridgway, 2003; Nichols, 2009), 两者之间为互相补充、相互支撑印证的关系, 或者说层序地层学是地层学与沉积学相结合在石油勘探过程发展起来的一门新兴学科。

Allen(2017)强调了沉积物输送体系是重塑各区段侵蚀和沉积地貌以及长期地质历史记录的关键, 乃沉积学研究的重中之重, 将它们联系起来则需要综合能力和独创性。纵观近十余年来关于源-汇系统的研究成果与认识, 可以发现这一理论性认识具有4个突出的特点: (1)强调沉积体系形成的完整过程, 聚焦于构造与气候的驱动机制、古物源区与古地形的演化以及古水系的重建(Armitage et al., 2011; Bentley et al., 2016); (2)重点分析沉积物输送体系对供源区与汇积区所产生的纽带作用(Allen, 2017; Caracciolo, 2020); (3)注重沉积动力学机制及碎屑物质分布的研究(Lajeunesse et al., 2010; Cai and Zhu, 2011); (4)突显沉积过程的量化表征, 核心在于构建物质通量或沉积过程动力机制的定量模型(Brenna et al., 2021)。可以看出, 沉积物输送体系是“源-汇”系统研究的核心内容, 其动力学过程受控于供源区构造、气候背景及搬运过程等因素。然而, 碎屑岩沉积体系的形成是地球表面侵蚀、搬运及沉积的一个完整势能均衡作用的体现, 具有高部位削截、低部位充填的趋势。从物理学角度而言, 沉积物的搬运应符合能量最低原理, 即碎屑物质沉积后, 处于最稳定的状态, 其势能最低。沉积颗粒在搬运过程中受到各种流体的作用, 其流体按照流动方向可以划分为3种类型, 即单向(河流)、双向(潮汐)和多向(波浪、底流和等深流)流体(Hayes, 1980; Ashton and Giosan, 2011; Geleynse et al., 2011)。McLaren等(2007)认为沉积物粒度作为搬运过程最为敏感的响应因素, 其在河流、滨岸—三角洲以及陆架—深水沉积中与坡度具有较好的响应关系。Yu等(2012, 2013)利用内蒙古岱海湖30多年的研究与Cogan和Gratchev(2019)利用大量水槽实验研究, 认为地形坡度及其坡型是控制碎屑物质沉积过程及其空间分布的主要因素。虽然不同流体形成的沉积体系, 其碎屑颗粒与坡降耦合效应的表现形式不尽相同, 但是总体规律是粒度随着能量或坡度的变化而变化的。

作者着重讨论陆源碎屑沉积体系的粒度与坡度之间的响应关系, 由此揭示碎屑岩沉积体系中, 流速变化情况下碎屑颗粒质量与坡度的定量关系, 这是因为当碎屑颗粒的密度基本不变的情况下, 其大小与其质量呈正比(质量=密度×体积)。碎屑沉积物在不同坡降下, 随着流速或流态与负载方式的变化, 形成沉积体系的相带(或河流的不同河段)发生变迁, 并在其三维空间产生不同的地质响应, 尤其是粒度随坡降的沉积分异作用、垂向结构或沉积序列、剖面叠加样式以及平面展布形态等。碎屑物质分布是随地形坡降变化的这些地质响应的总和, 作者将其定义为“物-坡”耦合效应, 因不同粒度在沉积物中的占比构成了沉积物类型的差异, 因此, 作者用碎屑颗粒的大小(粒度)来表征物质质量, 用地形变化的梯度来反映坡度与坡型的变化。故将“物-坡”耦合效应定义为“不同质量的碎屑颗粒在其搬运过程中随着地形坡降的变化, 经流速或流态与负载方式的转变, 最终在沉积区形成具有特定碎屑颗粒组成(N/G)及其三维空间展布特征的各种沉积地质体响应”。

2 自然沉积现象与问题思考
2.1 沉积现象及其解析

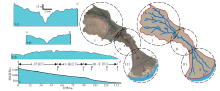
从大自然沉积现象来看, 陡坡主砾、缓坡多砂、湾者为泥, 可以说这就是碎屑物质质量与地形坡度耦合效应的选择性沉积结果, 即“物-坡耦合”效应的动力机制与碎屑物质经机械分异作用的具体表现。从现代沉积的实例就可以发现, 当地形坡度(降)较大时, 无论何种粒径, 近源沉积体的平面形态均以扇形为主(图1-a, 1-b)。此外, 当坡降中等时, 则沉积体以中粗粒的碎屑物质为主, 且形态多为扇形—帚状, 多具有限制性地貌, 惯性作用向摩擦作用快速转换, 并趋向呈帚状(图1-c, 1-d)。而当物源供给以砂砾为主且流速较大时, 尽管宏观形态基本上为扇形, 但辫流坝则相对发育, 由于粒度相对较粗, 因而以摩擦作用为主(图1-c)。当坡降较小时, 即使供源存在粗粒组分, 因流速不足以使其搬运, 粗粒沉积物在上游就已选择性沉积, 此时较为顺直的干流水道已分散成弯曲的支流, 以摩擦作用为主, 在下游则形成以细粒为主的沉积物(图1-e, 1-f); 当下游地形近于平缓且粒级小于4φ(<0.0625 mm)时, 碎屑物质由底负载转换为悬移负载, 致使前端朵叶体更发育, 并形成舌形体(图1-f)(Dade and Friend, 1998)。

图1 不同地形坡降下碎屑物质平面展布样式的野外自然景观实例
a和b—陡坡降(坡度>10°)的沉积体, 分别为富砾与富泥质沉积体的平面形态, 沉积营力主要为惯性; c和d—坡降中等(10°~5°)的沉积体, 分别为富砂与砂砾质沉积体展布样式, 沉积营力以惯性向摩擦力过渡; e和f—坡降较小(<5°)的缓坡沉积体, 分别为砂泥与富泥质沉积体平面样式, 沉积营力为摩擦向浮力过渡; g—左侧坡降较小, 为曲流河, 右侧坡降较大为辫状河; h—对应坡降由小变大, 上游为山间河流, 下游为冲积扇, 展示不同坡降背景下河流沉积的差异, 扇上发育辫状河, 而扇下则形成横向曲流河Fig.1 Examples of natural landscapes in the plane distribution pattern of clastic materials under different slopes

这些现象反映出, 由于碎屑物质颗粒的质量不同, 其搬运所需要的能量大小与类型各异。碎屑物质在某种坡降下, 经过侵蚀、搬运及沉积三大过程, 最终会形成对(相)应或特定碎屑物质组成(粒级分区)在三维空间的分布。但当坡降、可容纳空间及沉积环境均相同时, 由于物源供给的碎屑粒径不同, 其沉积结果则也可完全不同。这种碎屑沉积的总体分布规律反映出沉积物粒度的粗细与地形坡度大小呈正相关。需要指出的是, 当供源为细粒富泥的碎屑物质时, 无论坡度多陡和何种运动方式, 都不可能形成富砾与富砂的沉积体(图1-b), 如泥流; 但其形态仍与陡度有较好的对应关系。就山麓沉积而言, 当地形由缓变陡时, 山间河流进入盆地的山前则多形成各类扇体或扇三角洲沉积体系, 由此构成上游先陡后缓的古地形, 多发育(限制性)山间河流; 而下游发育各种扇体沉积并形成先缓后陡的地质景观(图1-f)。

从宏观上来讲, 河流沉积同样受到坡度的影响, 相同宏观背景, 坡降不同则河流的性质也不同。图1-g右侧河道坡降较大时, 河道以辫状沉积为主, 粒度以细砾和粗砂为主, 河道弯曲度较小, 各种沙坝占主体; 而左侧地形坡降明显小于右侧, 河道以曲流河或曲—辫转换沉积为特点, 粒度以中粗砂为主, 河道弯曲度较大。此外, 地形由缓变陡, 输送体系从相对较缓的山间或泛滥平原进入汇水盆地时, 则多形成各类扇体与三角洲沉积体系。就山麓沉积而言, 上游发育限制性山间河流, 下游发育冲积扇沉积, 对应不同坡降背景下河流沉积的差异很大, 扇上坡度陡发育辫状河, 而扇外缓坡则发育方向相差90°的曲流河(图1-h)。这些大自然的沉积景观, 诠释了碎屑岩沉积体系具有“陡坡惯性多扇帚, 水道偏直主粗粒; 缓坡摩擦道弯曲, 细粒悬浮端朵体”的特征以及粒径随坡降由大变小演化的基本沉积规律与沉积分异作用, 这些现象很难用水槽实验进行全面的模拟(Allen, 2017)。

2.2 问题的提出

为了预测碎屑沉积物的粒度分布规律, Sternberg(1875)就提出了颗粒的粒径随搬运距离增加而减小, 并建立了基于指数关系的距离与粒度方程(D=D0e-ax, 其中D为粒径, D0为初始粒径, x为搬运距离), 这一规律应存在2种成因解释: (1)较大的颗粒随着搬运距离的增加会逐渐磨蚀成细小的颗粒, 即颗粒间的碰撞会使碎屑物质的分选变好; (2)随着搬运距离的增加, 水流能量与地形坡度的降低, 会伴随着沉积物发生机械分异作用, 这是由于物质质量的大小差异而造成先后有序的选择性沉积。从公式来看, 距离x的起点是沉积中任意一点, 主要是计算一段距离内粒度的变化。Sternberg只是考虑了单向水流, 而没有考虑沉积物后期陆上风力与汇水盆地中波浪或潮汐等对沉积物的改造, 为此后人对其公式进行改进, 认为基底(底床)摩擦、负载方式及沉降速率均可以影响碎屑颗粒的搬运过程与粒度的分异。其研究也均是从单向水流实验观测的经验公式出发, 对颗粒的运动过程进行分析。

尽管Sternberg提出的观点已有一个半世纪, 但其数理方程仍是至今在力求破解的焦点(Ashworth and Ferguson, 1989; Wilcock and Crowe, 2003)。其原因有: (1)碎屑颗粒随着搬运距离的增加而粒度变细是一个总体规律, 当物源供给存在差异或有多物源供给, 如大型河流由多条支流汇聚而成时, 这个规律是无法或不能从整体上得到充分体现, 也就是说不能从源到汇笼统而论, 因供源区与汇积区沉积物输送体系(河道的作用)有所不同, 其表现形式各异。(2)碎屑物质在搬运过程中总体是从高向低的运动, 但不同坡降下的流速不同, 颗粒受到的基底摩擦、负载方式及沉降速率也不同, 加上碎屑物质在流体中的运动是矢量, 颗粒除受到的基底摩擦与负载方式的影响外, 还会发生相互碰撞, 其结果是颗粒变细的速度与机械分异作用产生的粒度分选特征也随之发生变化, 致使在汇积区形成具有特定粒度组成(粒度分布)及其三维空间展布特征的沉积体系(Reading and Richards, 1994; Ferrer et al., 2015; Boudet et al., 2017)。这一过程十分复杂, 难以给出具体的数学方程解。

为了进一步简化, 作者将从单向水流碎屑物质原始搬运与沉积动力所造成的结果入手, 来推导碎屑颗粒随坡度变化的运动规律。为此, 提出“物-坡”耦合效应的概念与相应的基本原理, 即沉积体系内部(汇积区)碎屑颗粒的质量随坡度与流速变化所产生的机械分异作用与地质响应。

3 “物-坡”耦合的理论基础与数理推导

机械沉积作用的基本组成因子是碎屑颗粒, 其粒度与结构不仅是区别于其他岩石的最基本特征之一, 更是沉积动力学研究的主要对象。沉积物的搬运和沉积, 是碎屑颗粒组分在流体介质(水或空气)的驱动下发生在某种对应地形坡降下的一种动力学过程。根据沉积物的颗粒性质与成因标志, 定量地重建或恢复沉积环境的动力学, 是多少代沉积学家的梦想(何起祥, 2010)。

3.1 理论基础

如何用数理的方法来诠释上述“物-坡”耦合效应的地质规律与成因机制, 一直是沉积学不断追求的目标。然而, 目前国内外的研究文献可证明的是, 碎屑岩沉积体系的平面形态大多受控于地形地貌特征, 尤其是地形坡降或变化方式的控制; 而剖面加积型式则是碎屑颗粒组成与坡度的相互耦合结果(于兴河, 2002; Mclaren et al., 2007; Patruno et al., 2015; 蒋恕等, 2022)。

3.1.1 水流能量与粒度 沉积动力学研究先驱者之一的巴格诺尔德(Bagnold, 1986), 从风砂沉积动力学研究入手, 再通过水槽实验和实地泥沙运动的调查, 于1941年提出了“水流能量”(Stream Power, 即水流速度与底床剪切力的乘积)的概念, 界定了床沙载荷(推移质与悬移质)的沉积动力学特性及其差异, 为古代沉积环境边界条件的定量描述奠定了当代沉积动力学的基础(何起祥, 2010)。大量的研究发现, 沉积物的粒度分布是水流能量的函数, 二者通常呈现正相关, 但具体而言是一个复杂的多变量函数。人们通过数理统计的方法研究沉积物的粒度分布, 用一些统计学参数来限定和描述沉积物的特征, 如特拉斯克分选系数(Trask, 1959)与维希尔的粒度概率曲线(Visher, 1969)等, 由此形成了描述沉积物粒度特征的一系列参数和粒度分布图版, 用来帮助人们分析它们与沉积环境之间的动力学联系, 这就说明碎屑岩沉积体系研究的核心指标之一是粒度分布。

然而, 在单向水流作用下碎屑物质的沉积行为同时受到2种力的制约:一种是颗粒自身的重力, 取决于颗粒的质量; 另一种是介质对颗粒的拖拽力(牵引力)或运动介质的惯性力, 取决于地形坡度、介质的密度、黏度、流速、水流深度及颗粒形态。而惯性力是物质质量的函数, 当系统存在加速度a时, 则惯性力的大小遵从: F=-ma(m为物体质量)这一基本原理。当颗粒所受的重力(或摩擦力)大于介质的拖拽力时, 发生沉积; 反之就发生搬运。这就是从牛顿第一定律引伸出来的斯托克斯定律(Stokes, 1851), 也是沉积学家最早用来探索粒度的沉积动力学意义的理论依据。正因如此, 重力与拖曳力的相互作用, 表现在颗粒质量与流体密度。碎屑颗粒质量的大小, 是决定其运动方式的关键所在(韩其为和何明民, 1979)。

3.1.2 沉积物的组成及分类 碎屑颗粒的质量或粒径大小不仅决定了其运动方式, 也是沉积物类型划分的核心依据。Reading和Richards(1994)在研究海底扇时就将碎屑沉积物划分为4种: 富砾、砂砾、富砂以及富泥型, 由此展现了各类海底扇平面形态与沉积物类型的相应关系。由于他们研究的是深海沉积, 故将砂泥质与富泥质划归为同一类型, 但这2种沉积物类型, 无论是搬运机制还是在平面的展布形态, 都有着明显的差异(图1-e, 1-f)。为了全面反映陆源碎屑沉积体系的碎屑颗粒组成的展布特点, 作者将碎屑物质按其主要粒径分布及其占比分为富砾、砂砾、富砂、砂泥以及富泥型5类(表1)。作者认为碎屑物质划分的依据应更多关注其搬运方式, 由于细粒(<0.0625 mm)的颗粒在水流作用下以悬浮搬运为主, 其沉积过程与中、粗粒明显不同, 其沉降速率差异较大(Udden, 1914; Wentworth, 1922)。因此, 限于篇幅, 在文中重点讨论富砾型—砂泥型沉积体的沉积过程。从自然沉积现象不难发现(图1), 不同坡降下碎屑沉积物的类型各异, 但总体是坡降越大沉积物的粒度越粗, 反之亦然。

表1 碎屑沉积物的分类、依据及其物理参数 Table 1 Classification of clastic sediments and its physical parameters

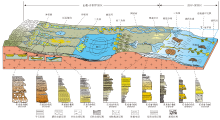
3.1.3 “源-汇”的输送系统及其地形地貌特点 沉积物输送系统从源到汇的地形变化可视为一个从供源区到汇积区的“天然沙漏”(Allen, 2017), 该“沙漏”具有明显的不对称性, 以侵蚀作用为主的上半部与以沉积作用为主的下半部的比例范围通常为30︰1到3︰1。大量的“源-汇”体系沉积地质实践研究可以发现(Wood, 1942; Sømme and Jackson, 2013; Lin et al., 2015; 操应长等, 2018), 在典型“源-汇”系统中, 上游流域(供源区)多表现为树枝状支流水系, 沉积物及水通过这些支流体系汇入干流, 即输送区(图2); 然后, 再通过这些干流直接进入下游流域(汇积区), 则呈现相反的树枝状分支水系。

图2 “源-汇”体系中供源、输送及汇积3个区域的基本形态特征与地质景观(以新疆克拉玛依柳树沟为例)Fig.2 Basic morphological characteristics and geological landscape of the three areas of source, transport and sink in “source-to-sink”system(taking Liushugou in Karamay, Xinjiang as an example)

由此可见, “源-汇”体系的纵向地形与横向地貌特征存在着明显的差异: (1)供源区纵向坡型为下凹型, 坡度由陡变缓(图2-L的A-B段), 横向地貌为负向单元-V型(图2-T-①), 排水支流逐渐汇聚, 以侵蚀作用为主并产生大量碎屑物。 (2)输送区的纵向剖面可以多种, 但主要为线型或下凹型(图2-L的A-B段), 横向剖面结构与供源区类似呈较浅V型(图2-T-②), 主干水道携带碎屑物向下游搬运。(3)汇积区纵向坡型则为上凸型, 坡度先缓后陡(图2-L的B-D或B-F段), 横向剖面的特征为正向单元(图2-T-③), 沉积物进行大量的卸载, 使干流水道向分支水道转变。正是由于横向地貌单元的不同, 才造成了水流或输送系统的分叉与合并(Parsons et al., 2010), 供源区因负向地貌而使支流合并成干流; 反之, 汇积区则因沉积物的堆积构成正向地貌单元或地势突然开阔而干流分叉成支流, 这就构成了“源-汇”系统中地貌对沉积物输送方式(子系统)的控制作用与分区(表2)。为此, 作者依据其输送方式, 将其划分为3个子系统, 分别为: 汇聚—补给、路过—搬运以及分散—卸载输送系统。

表2 沉积物输送系统的划分及其各自的特点 Table 2 Division of sediment routing systems and their respective characteristics

1)纵向斜坡型式

总体上讲, “源-汇”纵向剖面的古地形可以简化为3种基本型式的斜坡(Wood, 1942; Fryirs and Brierley, 2012): 线型(Liner: 角度总体不变)、下凹型(Concave up: 坡角逐渐变小)及上凸型(Convex up: 多为线型与下凹型的组合), 也称反“S”型。

早在1942年Wood就将地形斜坡划分为4种基本类型: 其区别就是他将线形斜坡进一步划分成顺直型(Straight)与陡崖型(Cliff)(Wood, 1942)。就线型斜坡而言, 自然界并不存在角度绝对不变的单斜—线型斜坡, 而多为角度变化较小的下凹型斜坡, 是一种近似的概念。

2)横向地貌单元

当分析横向剖面时, 通常描述的重点是其地形的形态特征, 即地貌单元。因此, 可将其划分为2种基本单元: 负向单元(下凹)和正向单元(上凸); 前者又可进一步划分为: V型、对称与不对称U型以及W型; 而后者则可划分为: Λ 型、对称与不对称上凸型以及M型。横向地貌的基本形态决定了水流的方向与沉积物的输送形式(表2)。负向单元多为断层与侵蚀作用的结果, 为沉积物的输送通道; 而正向单元则通常为沉积作用所形成的地貌单元。

除地貌对水流合并与分支具有控制作用外, 流速的高低, 即搬运能量强弱也是输送体系的控制因素。供源区流速逐渐加快, 能量增强, 侵蚀支流向低势能点汇聚成干流。而汇积区则相反, 流速逐渐减小, 能量变弱, 沉积物卸载造成阻碍, 干流分散成支流(图2)。流速的变化, 究其根源, 也是地形坡度变化所致, 从源到汇呈现出先加速再减速的过程。因此, 从源到汇横剖面的结构与地貌单元特征均具有明显的规律, 从供源区的W型→U型或V型→上凸型→M型的过渡(图2; 表2)。

3.1.4 坡度的定义与类型 纵观国内外近年来关于沉积体系水槽实验的文献不难发现, 大多采用的是沉积体系沉积前的底床坡角, 作者将其定义为沉积前坡角(即古地形坡角); 而现代沉积的研究则多为沉积后的地表坡角, 定义为沉积(后)坡角(于兴河等, 2018)。两者之间存在明显的差异, 前者是构造因素由风化侵蚀作用所造成, 在进行沉积学研究时需要进行古地形的恢复, 才可以得到; 而后者是由沉积物的堆积结果所形成, 反映沉积方式, 通常可以从其沉积构造或纵向剖面结构得到。然而, 沉积前的地形坡角才是控制因素, 需要指出的是坡角的大小随着地形的变化而改变, 文中坡度则是某一段距离的平均坡角; 此外, 沉积体系的形成通常存在多个期次, 前一期形成的沉积体表面是后一期沉积的古地形, 即前一期的沉积后坡角是后一期的沉积前(古地形)坡角, 这不仅对分析沉积体系的剖面结构, 即沉积物的叠加样式至关重要, 而且也是层序地层划分级次的核心判别依据。为此, 就沉积成因分析而言, 作者主要讨论的是顺水流方向(纵向剖面)的沉积前坡角, 着重分析纵向剖面一期沉积的加积型式, 而非多期的叠加样式。

关于坡度陡、缓在沉积学中并没有一个公认的确定性界线, 实际应用中多是地质上的描述性语言, 而非严格的数学—物理学概念。其具体的划分标准, 因不同沉积体系所处的位置不同而存在差异。其中以山麓段沉积为例, 经Reitz 和Jerolmack(2012)利用水槽实验对冲积扇体系的沉积休止角研究, 提出10°为其划分缓坡和陡坡的临界角度; 同样Prior等(1989)对环墨西哥湾三角洲进行研究时则提出5°为其划分陡坡和缓坡的边界。从大量的现代沉积事件的稳定性来看, 实际野外地形坡度通常在1.5°~25°之间, 坡度系数(高差与水平距离差的比值: 纵横比)最大约为50%(李树芳, 1993)。而从环境学对地质灾害可能发生不稳定的环境与大量野外考察的经验出发, 是将坡度系数(纵横比)为25%作为划分界线, 在沉积学中人们通常将坡度划分成陡坡与缓坡两大类, 陡坡进一步分为陡峭、极陡及较陡, 而缓坡则可分成较缓、平缓及平坦。以上都是依据具体的实例所得出的某个地区的认识, 并没有严格的界线或具体数值。这就可以看出, 从“源-汇”的角度而言, 不同区段或沉积体系不能用同一个划分标准, 而应给出相应的划分方案以体现各区段的特色。

3.2 数理分析与模拟结果

3.2.1 数理分析 从内部因素而言, 单向水流碎屑物质的沉积实质上就是一定的坡度与流速下, 某种质量的碎屑颗粒从无法被搬运的静止状态到被搬运的运动状态, 再到搬运不动的沉积状态。因碎屑物的流速变化决定其静止状态, 为了表征前述汇积区沉积体系内“物-坡”耦合的效应, 首先要推算或判定何种流速与坡度下不同质量颗粒的静止与被搬运的临界点。通常碎屑沉积的流动或搬运过程将颗粒与水视为整体, 从重力势能向动能的转换角度建立了流速公式。但要建立碎屑颗粒质量与坡度开始运动前的静态平衡关系, 则需要将流体中的颗粒与水分开来考虑, 以便更好地对斜坡上静止的颗粒进行受力分析并建立相应的推导过程, 在颗粒依然保持静止的临界条件下, 探讨坡度、水流速度对不同粒径颗粒的搬运与沉积的控制作用(图3)。

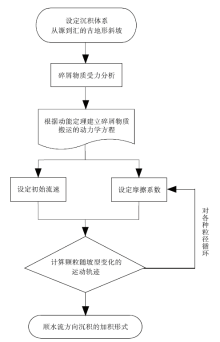图3 “物-坡”耦合效应沉积正演模拟流程图Fig.3 Flow chart of the depositional forward simulation of “mass-slope”coupling effect

静态受力平衡与动态能量转换是沉积物运动的2个阶段, 静态平衡的核心就是界定不同质量或粒径的碎屑颗粒被搬运的初始坡度与流速, 能量转换的响应则是一定地形坡度下流体搬运过程中的速度变化, 主要体现不同碎屑颗粒的搬运方式(滚动、跳跃及悬浮)与沉积物输送营力或动力的转换方式上(惯性、摩擦及浮力), 随着流速或能量的加大与变化, 碎屑颗粒依次从静止状态转变成被搬运状态, 在搬运过程中, 随着搬运距离的增加与地形高程的降低, 流速随之减小且势能逐渐降低, 当流速降低到无法搬运某种质量大小的颗粒时, 该类颗粒变为沉积状态, 这就是机械分异与选择性沉积的实质, 即沉积物形成的物理过程。

陆源碎屑沉积体系形成的地形坡降与碎屑物质之间的耦合效应在自然界普遍存在, 沉积物粒度的粗细通常与其地形坡度的大小呈正相关; 在一定的流速与地形坡度下, 不同质量的颗粒其沉积先后存在差异—沉积分异作用。它们符合能量(势能)随坡度减小而变化的基本原理。但其定量数学关系极为复杂, 碎屑物质的粒度分布特征(Ds)是颗粒与流水在重力(G)以及摩擦力(F)作用下的机械能损失及转换的结果, 是颗粒密度( ρs)、颗粒的大小(d)、水流密度( ρw)、颗粒运动速度( vs)、水流速度( u)、地形坡降( θ)、流态( Fr、Re)以及滑动摩擦系数( μ)、水流剪切摩擦系数(f)随搬运距离(x)的函数。

Ds=∫0x(ρs, d, ρw, vs, u, θ, Fr, Re, μ, f)dx(1)

无论是内容还是形式, 公式(1)都十分复杂, 可以说是学术界长期致力解决的焦点, 尤其是泥沙动动力学的研究与沉积计算模拟(齐亚林等, 2018)。作者为了简化计算过程, 将沉积物分解成不同大小的颗粒, 来分析某种颗粒搬运时流体的受力, 计算其速度的变化, 这样就可以忽略层流与紊流、亚临界流与超临界流的问题。由此可以忽略流态(Fr、Re)变化所引起的沉积物搬运方式的改变以及沉积物侵蚀或卸载过程所引起的流体密度( ρw)的变化; 而为了表征含有不同粒径沉积物的流体之间的差异, 需要考虑其所搬运颗粒的大小(d)、颗粒的密度( ρs)、颗粒与床底的滑动摩擦( μ)以及流水与床底的剪切摩擦( f)。模拟实际流体运动则需要考虑地形坡度( θ)和流体速度( u)。由于滑动摩擦系数( μ)是物体表面粗糙程度的函数, 碎屑颗粒的粗糙程度通常是磨圆度的函数(Alberto et al., 2018)。就正常碎屑颗粒(-8 φ~4 φ)而言, 磨圆度随着粒度的变细而变好。因此, 粒径越大的颗粒其滑动摩擦系数越大, 滑动摩擦系数的大小可以表征流体所搬运颗粒的大小。为了体现流体运动速度与地形斜坡变化之间关系的总体规律, 公式(1)可简化为:

Ds=∫0x(ρs, u, θ, μ, f)dx(2)

由此可以说明“物-坡”之间的物理关系, 体现了碎屑颗粒质量( ρs, μ, f)、坡度( θ)以及速度( u)三者之间的关系。

3.2.2 正演模拟过程 采用沉积物搬运-沉积正演的思路, 模拟计算单向水流碎屑颗粒的运动过程, 设定步骤如下(图3): 尽管文章重在模拟汇积区的运动速度, 但需要从沉积物的输送区开始计算, 因上游流速的大小与变化直接影响下游流速的变化规律。

1)设定一个反映“源-汇”全过程的总体地形斜坡, 用6次一元方程的数学函数表征其地形的变化: h=a1x6+a2x5+a3x4+a4x3+a5x2+a6x+a7, h为高程;

2)在设定的总体地形斜坡上, 对碎屑颗粒作受力分析: 重力G=mg, 摩擦力F=μ mgcos θ + 18·ρ fu2S, 依牛顿第二定律得到:mgsin θ -μ mgcos θ - 18ρ fu2S=ma, 取单位体积(体积为1, 截面积S为1)进行分析得到gsin θ -μ gcos θ - 18fu2=a; 其中m为流体质量, g为重力加速度, μ 为流动过程中颗粒与底床的滑动摩擦系数, ρ 为流体密度, u为流体速度, f为剪切摩擦系数(Fanning, 1877), S为截面积。

3)搬运过程能量守恒, 依据动能定理, 建立速度公式:

∫ugsinθ-μgcosθ-18fu2du=∫dx(3)

其中, g为重力加速度, μ 为流动过程中颗粒与底床的滑动摩擦系数, u为流体速度, f为剪切摩擦系数(Fanning, 1877), x为位移。

4)设定初始流速u与摩擦系数μ 、f。初始流速的设定应反映该沉积体的供源区的流量, 不同地区的沉积体应设定不同的数值, 本次设为1 m/s。滑动摩擦系数的计算, 根据恩格隆(Engelund)的对数阻力公式建立(Engelund and Fredsoe, 1982): 滑动摩擦系数与粒径的对数值呈正线性相关。对搬运不同粒径颗粒的流体设定不同的摩擦系数, 分别依次进行计算, 最终叠合得到沉积物的顺流加积特征。因不考虑流态的变化, 剪切摩擦系数f可以设为常数, 本文取0.06。

5)依据速度公式模拟计算地形坡度变化不同质量(粒径)颗粒对应的运动速度; 最后依据能量与颗粒质量的静态平衡, 判定不同质量颗粒在相应地形下开始沉积的位置与区域, 进而确定碎屑颗粒质量与地形坡度的耦合定量关系。

将边界条件设定为: u=u0, x=0, 带入式(3)得到:

u=e-fx4u02+8g(sinθ-μcosθ)f1-e-fx4(4)

该方程表达了地形坡度控制下碎屑颗粒运动速度随搬运距离的量化关系。初速度 u0, 滑动摩擦系数(μ )以及剪切摩擦系数(f)为可调节参数。

3.2.3 速度模拟计算 为了便于从沉积动力学上来分析陆源碎屑岩沉积体系从源到汇的全过程, “源-汇”体系从的总体特点来分析前述3种基本地形斜坡组合的地质特征, 由此便可构成一个由陡到缓—由缓变陡再变缓的总体地形斜坡(图4-a), 该地形可以涵盖陆源碎屑主要沉积体系(冲积扇、河流及三角洲)形成的古地形斜坡变化特征。其地形变化可以划分为5个区段:

图4 从源到汇纵向剖面总体斜坡特征及其流速模拟结果
a—自然界中斜坡样式的总体特征, 根据粒度分异可以将其从近源至远源依次划分为富砾、砂砾、富砂、砂泥及富泥型。沉积物与底床的接触关系也由下截向下切型转化; b和c—分别表示沉积/侵蚀能力以及坡度随着沉积物搬运距离的增加而变化, 横坐标为相对距离, 以输送体系起点为原点(干流的初始点), 以沉积体搬运最远距离为基准点(设为1)进行计算, 超出部分为悬浮沉降部分; d—曲线为分别计算不同粒径速度后叠合的结果, 并非多种颗粒混合流动, 因此不需要考虑颗粒之间的相互作用。图中的断开符号表示供源区的范围通常更大Fig.4 General slope characteristics from source to sink and its flow velocity simulation results in the longitudinal profile

A-B段为供源区, 通常为由陡变缓的地形斜坡(图4); 主要发育限制性水道, 多为山间溪流(stream)或支流(tributary), 这些河流的间歇性或季节性特征很强, 此段沉积物输送系统的核心作用, 是通过各个方向的支流将碎屑物质聚集到主干水道之中, 在空间上表现出支流汇聚成干流(trunk)的地质景观(图2-I)。然而B点为供源区支流聚集成干流的陡—缓转折点, 通常是干流的起点, 由于大量支流的汇聚, 流量增加其流体开始加速; 因此, B-C段为沉积物的主要输送区, 通常为线形斜坡, 坡度的陡缓不同地区存在较大的差异, 通常可形成下切谷, 侵蚀略大于沉积, 多数情况下基本处于平衡状态。而C点为坡折点, 是沉积物或流体再次加速的位置, 也是搬运过程中最不稳定的位置(图4-b), 因此, 此点通常并不发生沉积, 只是路过。C-D段由于坡度在逐渐增加(图4-c), 所以大多数情况中细粒碎屑颗粒在此并不发生沉积, 主要为水道的侵蚀区, 以侵蚀/路过为主; 就大陆架而言此段称为坡折带; 就山麓区而言, 此段通常易发生碎屑流(或泥石流), 因其下部往往是巨型颗粒停滞的区段。

因而, A-B段是一个从地表遭受侵蚀到碎屑物质加速搬运的补给区段(图2; 图4-b), 从能量上来讲, 此段是能量聚集的过程。D点为坡角最大的转换点, 其上为坡角的增加, 而其下为坡角的减小(图4-c), 是以由侵蚀为主转变为沉积为主的转换点(图4-b)。所以, D-E段是沉积物快速沉积的主要区域, 并以惯性作用为主; 就冲积扇与三角洲而言, 是由河流作用所形成的冲积平原或三角洲前缘发育的地形背景, 但就河流来讲, 则是辫状河发育的主要区域。 而E-F段为相对缓慢的沉积区域, 其地形反映了各种非限制性中—高弯度水道发育的地质特点, 以摩擦作用为主, 若进入汇水盆地, 则为前三角洲形成区, 则以浮力作用为辅。因此, D-F段(由陡变缓的下凹型斜坡)是沉积物的主要卸载—沉积区, 即汇积区的核心区, 是能量散失的过程。其沉积物输送系统的主要作用是将碎屑物质分散到各处沉积下来, 表现出从干流向多方向转变成支流(分流河道)的地质景观。再向下游的区域则通常为水流作用下难以波及的汇水区(图4-E-F段), 也可以说是扩散作用造成悬浮物质沉积的主要区域, 或地形再次变陡, 而在远端的水下发生沉积物重力流沉积的区域。

3.2.4 模拟结果

1)“物-坡”耦合的加积型式

基于方程(4)计算得到不同颗粒速度曲线(图4-d), 由此揭示出, B-D段随着地形坡度的逐渐增加, 能够搬运的颗粒粒径逐渐增大, 同时颗粒的运动速度也逐渐加快; D-F段速度在D点下游短暂增加(惯性的原因)后, 随着地形坡度的逐渐变小而逐渐降低, 最终不同粒径的碎屑颗粒沉积在特定的位置, 从粗到细其速度曲线表现出先密后疏的特点, 反映了细粒的物质较粗粒搬运的距离更远, 速度曲线呈现出明显的抛物线型, 与底床的接触关系由高角度下截逐渐转换为截切转换、高角度下切及低角度下切, 直至平行, 其沉积物相应的由富砾型—富砂型直至富泥型的逐渐变化, 且单层厚度逐渐减薄, 这一规律反映了陆源碎屑沉积体系在纵向剖面碎屑物质顺流加积的主体加积型式。

2)粒径与坡度耦合关系

速度曲线的计算本质是一种数值计算, 误差主要取决于计算采用的距离步长。该步长决定了最终读取颗粒沉积位置的精度, 步长越小计算精度越高, 计算步长采用0.002时, 计算得到的散点图拟合程度高达99.88%以上, 达到了地质解释的计算要求。

根据模拟计算结果, 从数理上论证了沉积物类型与地形坡度之间的“物-坡”耦合关系(图4; 表3), 陡坡、缓坡可以用坡度系数(纵横比)15%为界来划分; 陡坡可进一步划分为陡峭(坡度系数>40%)、极陡(40%~25%)与较陡(25%~15%)3种, 缓坡进一步分成较缓(15%~10%)、平缓(10%~2%)及平坦(<2%)3种, 坡度系数是根据大量研究的统计得到的宏观概念, 强调的是范围, 其对应的坡度值并非整数值(表3)。因此, 正常流水情况下, 沉积物类型与地形坡度之间具有较好的对应关系。为了便于今后的讨论, 提出按沉积物类型并用坡度系数对坡度进行划分, 即粗粒沉积物的坡度系数多大于15%, 以此作为划分其坡度的依据与范围, 而中粒与细粒沉积体则分别以10%与2%作为划分依据。

表3 沉积物类型与坡度(坡度系数)的关系 Table 3 The relationship between sediment type to slope (slope coefficient)

统计颗粒粒度与其沉积位置处的坡度(图4-d), 得到了粒度的平面分布特征函数, 粒度与坡度呈现出明显的指数函数关系, 其“物-坡”耦合的数学表达形式为:

D=aebθ(5)

其中, D为颗粒的粒径(mm); θ为坡度(°); a为粒度参数(坡度为0时, 对应的粒度), 反映了沉积体发育的最小粒度; a值的大小反映了沉积体在惯性作用下向前推进的强弱, 也反映了沉积体整体的粒度粗细特征, 是受力结果的物质表现。b为地形参数, 代表了地形坡降的快慢, 以及单位坡降下粒度变化的差异大小。b值越大, 地形坡降变化越快, 沉积体延伸范围越小; b值越小, 地形坡降变化越慢, 沉积体延伸范围越大。a与b分别代表了沉积体的物质层面与地形层面特征, 是“物-坡”耦合作用的表征参数。该公式(5)是Sternberg(1875)观点与假设的修正与发展。

4 “物-坡”耦合效应在三维空间的地质响应

McLaren 和 Bowles(1985)认为沉积物粒度是搬运过程最为敏感的响应因素, 其在河流、滨岸—三角洲以及陆架—深水沉积中与坡度具有较好的响应。针对一个完整“源-汇”体系提出的碎屑岩沉积体系的“物-坡”耦合效应的规律与认识, 可用于各个级次, 旨在探讨“物-坡”耦合的地质响应及其沉积地质特征的表现。作者从点(垂向粒序)、线(剖面结构)、面(平面展布)3个维度来阐述碎屑岩沉积的“物-坡”耦合关系, 并从沉积物搬运原理与输送营力的角度对其沉积成因与空间展布特征进行解释。

4.1 垂向沉积序列特征

通过对大量的研究不难发现, 无论何种沉积体系, 都是由多个垂向沉积序列所构成, 这就是沉积旋回, 它反映的是沉积体系本身或相带的变迁规律与演化。而垂向序列则是由不同的粒序所组成, 因此, 粒序通常指某一期沉积在某一点形成的垂向基本单元, 即粒度在垂向上的变化, 是沉积物输送动能变化的产物, 由此造成粒度与沉积速率的变化, 而岩心与野外分析的重点就是垂向沉积序列, 也称相序, 是同一沉积环境下沉积(微)相变迁所形成的岩相组合, 通常有5个要素: 岩性(粒度)、厚度规模、沉积构造、生物及颜色。广义上讲, 这些要素反映的是水动力条件的变化; 严格来说, 则是地形坡降变化所造成搬运能量与水深的变迁, 致使碎屑物质产生选择性沉积。总之, 垂向沉积序列是多种沉积营力(河流、波流及潮汐)作用下沉积环境变迁的结果; 在不考虑气候的情况下, 上述要素都是“物-坡”耦合作用的结果。

因此, 垂向粒序或相序是不同沉积作用与加积方式的响应, 就一次性沉积而言, 主要受坡型样式的控制。从沉积学上讲, 垂向粒序实质上主要有3种基本形式: 即向上变细的正粒序、向上变粗的反粒序以及粒度无明显变化的均质粒序。由陡变缓(下凹型斜坡)通常造成水体加深形成退覆式沉积, 水道正切则形成具有正粒序结构的负向地貌(例如河道等)单元; 而由缓变陡(上凸型斜坡)过程正好相反, 水体变浅通常形成具反粒序的正向地貌(坝体或扇体等)单元; 层序地层学的观点是水体的进退(海平面的升降)为主因, 但下凹型斜坡水进表现比上凸型更为明显, 反之亦然。而地形样式不变的缓慢沉积, 则主要表现为似均质粒序(图5)。这就是用垂向沉积序列或测井相来分析沉积相类型的基本原理。然而, 从地质描述或测井相分析而言, 则将垂向粒序划分为4种基本的型式: 即钟型(正粒序)、漏斗型(反粒序)及箱型或指状, 箱型与指状均为似均质粒序, 前者是坡度较陡背景下快速沉积的结果, 分层不明显; 而后者则是坡度较缓背景下缓慢沉积的产物, 分层明显, 多为粉细砂与泥的间互。钟型为水道的沉积产物, 而漏斗型则为各种沙坝的形成结果。

图5 碎屑岩沉积体系粒序和坡度变化之间的关系Fig.5 Relationships between grain order and slope variation in clastic depositional systems

4.2 剖面叠加样式

从宏观角度上讲, 沉积物在剖面上的叠加样式存在2个截然不同的方向: (1)顺水流方向的纵向剖面, 不仅呈现出沉积坡型样式的转变(即由陡变缓或由缓变陡), 还可表现出进积、退积及加积的方式, 反映出沉积与沉降、水进与水退以及物源供给方式(如持续性或间歇性增加与减少, 以及稳定等)间的变化; (2)横切水流方向的横向剖面, 着重反映了沉积体形成前、后的地貌特征与沉积体系横向展布的对称性。

4.2.1 纵剖面的响应特征 主要表现为顺流加积(进积或退积)样式的差异。就单期沉积而言, 在纵向剖面上, 随着坡度的由陡变缓, 沉积体不同粒径的碎屑颗粒与底床的接触关系依次表现出下截、截切转换、高角度下切—低角度下切, 直至平行(图4-d; 图6)。这种关系同时也反映出从富砾型到富泥型5种沉积物类型的依次变化, 各类型的范围大小与坡度呈负相关。当坡度较大且沉积物持续供给时, 近源沉积为快速加积, 与底床的接触关系以下截型为主的特征(地震剖面上表现的更为明显), 以滚动搬运的富砾或砂砾型沉积物为主; 中部表现出由下截型向下切型的转换, 则以跳跃搬运富砂型沉积物为主; 而沉积体系的端部, 加积型式表现出叠瓦状或平行, 反映出以悬浮搬运的细粒砂泥型或富泥型沉积为主。

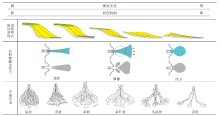图6 碎屑岩沉积体系“物-坡”耦合效应在空间上的表现特征与规律Fig.6 Spatial characteristics and patterns of “mass-slope”coupling effects in clastic depositional systems

对多期沉积而言, 则是以进积或退积的方式进行重复性叠加, 这取决于沉积速率与沉降速率的对应关系。需要指出的是, 三角洲沉积体系在坡陡时, 易形成吉尔伯特型三角洲, 通常具有三层结构, 即顶积层、前积层及底积层, 而坡缓时则底积层通常不发育, 地形极缓或平坦时, 则可能只发育前积层(图6)(于兴河等, 2013)。基于此, Vail等(1977)提出的海相经典大陆边缘层序划分方法: 低位体系域、海侵体系域、高位体系域, 以及Cross(1988)提出的高分辨率层序地层的基准面变化, 同样是坡型变化的地质响应, 其实质也是“物-坡”耦合效应在沉积演化过程不同时期的表现形式与沉积响应。

4.2.2 横剖面的响应特征 横剖面有正向与负向2种地貌, 正向地貌为上凸型, 主要表现2个方面: 在宏观上是沉积体系(各种扇体与三角洲等)横断面表面形态; 微观上则是各种沙坝的形态。它们大多是地形由缓变陡背景下由沉积物的不断顺流加积所致; 其对称性则主要取决于古地形横向的高低差异。然而, 负向地貌单元的形态为下凹型, 其形成主要受控于构造或水道的侵蚀作用; 地形越陡, 河道/谷越窄, 反之亦然。河谷或水道的宽窄与弯曲段的大小则受控于地形坡度、碎屑粒度组成以及流水能量。通常表现出辫状河粒度粗, 水道宽, 以沉积为主; 曲流河地形越缓弯曲度越大, 粒度与坡度呈正相关, 表现出沉积与侵蚀的平衡; 负向地貌(水道或河谷)的对称性通常取决于其弯曲度的大小, 弯曲度越大其对称性越差, 河谷或水道越直对称性越好。总之, 负向地貌的规模大小主要受地形坡降与物源供给量的控制, 而正向地貌规模则主要受流速与侵蚀能力的控制。

4.3 平面展布形态

沉积体系的平面展布形态通常反映了各类碎屑物质(含砂率N/G)与颗粒在平面上的聚散过程, 其几何形态主要有扇状、帚状、朵状、朵叶状、鸟足状及舌状等(Reading and Richards, 1994; 于兴河等, 2013, 2018)(图6)。平面形态和顺水流纵向剖面的地形坡度通常有良好的对应关系, 平面形态明显受沉积背景的古地形控制。地形越陡、粒度越粗, 平面形态越呈扇形; 随着地形的变缓, 上游的沙坝从菱形向舌形变化, 水道分叉, 弯曲度增加; 随着搬运距离的增加与地形进一步变缓, 水道切割加深, 堤岸更加明显; 洪水期水道下切速率低且流量大则可在水道弯曲处发生决口, 随之分支水道增多, 平面呈现出朵叶状, 就三角洲而言, 在其前端(前缘外侧)因地形进一步变缓, 则出现鸟足状或舌状, 前者为水道的进一步分叉, 后者为悬浮物的扩散。

5 “源-汇”体系中各区段“物-坡”耦合的地质响应特征

从宏观沉积来看, 从山麓的源头到湖盆或洋盆的深水区, 碎屑沉积物的特征均与各区段地形坡降变化有着密切的关系, Allen(2017)将“源-汇”体系划分成山麓、河流、滨岸(滨海)或三角洲以及陆架—深水4个沉积区段, 即各段可形成独立的沉积体系, 通常上游区段沉积体系的产物是下游区段沉积体系的供源区, 也就是说“源-汇”体系同样存在着级次。总体规律是每个沉积区段(体系)内, 碎屑粒度、垂向序列、剖面加积型式以及平面形态随着坡降的变化而呈规律性的分布(图7), 具体表现就是随着坡度的降低粒度变细。为了突显“物-坡”耦合效应的地质特点, 按照陆相与海相两大区分别进行论述, 即山麓—冲积平原区与滨岸—深水区。

图7 从源到汇不同碎屑岩沉积体系的地形坡降及其对应的垂向序列与平、剖展布特征Fig.7 Slape geodiet f diferemt clsic derositinal sysems from sure to sink and ther coresyonling vertiral seqyene, profle acretiom patlem and panar sreazing chanacterisces

5.1 山麓—冲积平原区

山麓段的“物-坡”耦合效应可以说是所有区段中最为突出的区域, 碎屑物在这一过程产生“物-坡”耦合效应并发生选择性沉积。然而, 其平面形态受地形坡度与沉积物的侵蚀/加积作用影响, 扇体大小不仅与供源区面积具有较强的正相关性, 而与坡度陡缓呈负相关。(1)从纵剖面和垂向序列上来看, 坡度越大, 碎屑流对扇体的控制作用越强, 其沉积在垂向序列中占比越高(图7①; 表4), 沉积构造特征越不明显, 粗碎屑物质的含量越高; 反之, 坡度越小, 细粒占比增加, 河道牵引流作用增强, 演化的期次性增多, 沉积构造的多样性增加。(2)从平面形态特征上看, 坡度越大, 表现出较规则的扇形沉积(图7; 表4), 且发育规模相对较小, 扇体表面河道特征越不明显, 反之, 扇体平面规模越大, 表面的河道越发育。随着坡度变缓、碎屑物质的粒度变细, 平面形态上冲积扇由扇帚状向朵体演化, 扇体的规模增大, 河道发育增强, 沉积前的古地形多为下凹型, 而沉积后的地形则多呈上凸型。

表4 各沉积体系中不同沉积物输送营力的“物-坡”耦合特征与粒序的基本关系 Table 4 Mass-slope coupling characteristics of different sediment-routing agent in various depositional systems

河流段的“物-坡”耦合效应表现为: (1)从剖面和垂向序列上讲, 坡度越大, 沉积物以惯性营力输送为主, 河流通常表现出砂砾组合的特点, 箱型的正粒序较为发育(图7②), 河道具有较大的宽深比, 细粒物质占比较低。随着坡度降低, 惯性营力全面向摩擦营力转化, 沉积物由富砾型向富砂型与砂泥型转化, 河流二元结构特征增强(图7③), 细粒沉积的空间占比增大, 反映低流态的各类沉积构造明显增加(图7③, 7④), 生物作用也显著增强。(2)而从平面形态特征来看, 局部的陡缓变化是造成河道分叉与合并的主要原因, 由缓变陡多分叉, 由陡变缓则趋于合并; 坡度越大, 河道越直, 河道横断面的对称性越好(图7), 由通常表现出辫状形态, 具有多条活跃水道和长条形心滩坝; 随着坡度降低, 河道的弯曲度增加, 截弯取直的过程使废弃河道的分布增多, 其断面的对称性越差。地形平缓或平坦时, 则可形成网状河, 因河道相对较为固定, 通常窄而深, 具明显的泥包砂特点。

尽管Allen没有将湖盆(泊)在其“源-汇”体系单独作为一个沉积区, 但它有着与海盆不同的地质特点。其分类方案很多, 但从其剖面上来讲, 尤其是短轴方向, 总是存在相对陡、缓差异的2种特征不同的地形斜坡(图7)。湖盆与海盆一样可发育多种沉积体系, 各沉积体系“物-坡”耦合的地质响应特征在其他区段均已论述, 不再赘述。但沉积有一个总体的规律: “陡坡小而多、缓坡大而少; 陡坡扇形水道少, 缓坡朵叶河弯多; 陡坡富砾快沉积, 缓坡多砂侧迁移, 湾者平缓沼坪泥”。

5.2 滨岸—深水区

滨岸带的陡缓与沉积结构具有紧密联系, 表现为: (1)从剖面和垂向序列上来看, 坡度越大的情况下, 前滨的沉积物以砾石及中粗粒为主; 淘洗作用使反粒序发育(图7⑥)。随着坡度降低, 粗粒沉积物质逐渐减少, 砂泥质、富泥质开始增加, 在近滨形成正粒序为主的沙滩。需要指出的是, 通常潮下带的能量比潮上带要强, 这多是地形下陡上缓的原因, 当存在障壁—潟湖时更是如此。总之, 坡度越陡, 波浪与潮汐对滨岸改造的作用越强, 沉积物的粒度越粗, 反之亦然; 一般来说坡度越小, 生物构造特征明显增强; 而在浪基面之下的深水区, 波浪与潮汐作用很难涉及, 沉积物泥质含量增多。(2)从平面形态特征上讲, 滨岸的宽窄、长短及弯曲度是坡度的函数, 陡窄、长、直, 缓宽、短、弯。当滨岸带坡度较缓且沿海平原越宽时, 沉积物越细, 分选越好, 反之沉积物越粗, 分选越差。

三角洲体系的发育受控于地形坡度, 表现为: (1)三角洲的纵向剖面和垂向序列可以说是所有沉积体系中地质特征最为明显的区域, 通常可以发育三层结构、具有明显的前积(或退积)叠加样式以及多具有正、反粒序交替的垂向序列(图7⑥—图7⑧)。前述的模拟计算结果已论述了其加积型式与三层结构发育与陡度的关系, 不再赘述。(2)从平面形态来看, 三角洲明显受沉积背景的古地形控制(图7)。地形越陡, 粒度越粗, 平面形态越呈扇形; 随着地形的变缓, 搬运距离的增大, 粒度逐渐变细, 三角洲的分流现象就越强。随着沉积坡度由陡变缓三角洲的平面形态由扇形、朵状向朵叶状或鸟足状转变; 分流河道的分叉频率增加, 河口坝的规模逐渐变小并消失, 这就是浅水三角洲因坡度过缓河口坝不易发育的原因。

陆架—深水段地形坡降的变化形式控制着沉积物输送的方式与粒度的粗细, 而物源供给的程度通常决定了深水水道沉积的规模大小。主要表现为: 从深水沉积体系的剖面和垂向序列上来看, 坡度越大的情况下, 粒度越粗, 深水扇通常表现出富砾或富砂的特点。砾石主要由碎屑流沉积, 砂质由高密度浊流快速沉积。富砂海底扇因海浪、风暴及潮汐作用可使碎屑物质分选变好, 去除大部分泥, 留下被浊流改造的富含砂质沉积物(图7⑨~⑩)。富砂质浊流搬运距离不远, 所以扇体很可能较小, 半径通常小于50 km(Reading and Richards, 1994)。沉积主要是由高密度的浊流所形成。砂泥型海底扇的直径为数十至数百千米, 由发达的河道—天然堤系统和沉积朵体组成。富泥海底扇, 由大型海底峡谷水道提供物源。坡度越低, 浊积水道弯曲度越大, 水道沉积多为粉砂质泥, 天然堤发育良好, 当地形突然再次变缓时, 则多易形成溢岸沉积。

6 讨论及展望

地形坡降类型(即坡型的变化)是“源-汇”系统中沉积物输送体系的核心要素, 尤其是对于具有近源快速堆积、粒度变化快、水动力复杂特征的粗粒沉积体系(Nemec and Steel, 1984; Nemec et al., 1984; 于兴河等, 2018)。坡型的变化, 既可以是空间上的转变(上游到下游的变化), 也可以是时间上的演化(早期到后期的变化), 对于绝大多数沉积体系而言, 早期的古地形为下凹型斜坡(由陡变缓), 沉积一段时间后则变成上凸型斜坡; 坡型的演变控制着沉积体系中不同沉积物在三维空间的变化与分布。同时, 它们也影响汇积区的范围与边界的位置(如沉积体系与岸线的划分), 沉积体内部的非均质性(如相带与粒度分布的划分), 在各种扇体、块体密度流及三角洲体系中尤其体现出坡型变化的重要性(Bhattacharya et al., 2016)。坡降类型的划分(由陡变缓与由缓变陡的变化), 也可进一步分成快速、缓慢及逐渐变缓与变陡, 对应的地质响应则可能是今后努力的方向。

Harvey等(2005)指出地形坡降可以表征可容纳空间的变化, 影响沉积物的供给量, 进而控制各类扇体表面的坡降与平面形态。因此, 古地形坡度(沉积前坡度)的计算是研究冲积扇、河流、三角洲等体系的主要沉积动力学参数(Bhattacharya et al., 2016; 于兴河等, 2018; Long, 2021)。古坡型特征的恢复对解释沉积体系的展布、内部构型以及重力流的发育均具有重要意义。如何在野外确定现代沉积的古地形坡度的变化, 以及古代沉积的古地形则成了沉积学长期以来的一个难点与瓶颈, 现代沉积可以通过古河道、探槽及探地雷达等方法得到, 但这些手段对其初始沉积的古地形研究往往存在的问题是其垂向深度不够, 这是未来需要解决的重点。而对古代沉积而言, 地震剖面的分辨率只是一个总体的概况, 对于不同级次沉积的坡型研究往往存在精度不够, 还有极大的提升空间。这些问题的解决将有利于解决“源-汇”研究中沉积物输送系统的变化与成因。

作者提出的“物-坡”耦合效应主要是指单水流作用下“汇积区”坡型变化或不同类型坡降下沉积物类型的总体响应规律, 而非具体坡度大小与粒度的绝对对应关系, 主要关注不同粒径颗粒之间的相对位置, 而与其沉积的绝对位置(距离大小)无关。然而, 不同沉积体系的“物-坡”效应相差甚大, 影响因素也较多, 也就是说在“源-汇”体系中各区段之间的坡度陡、缓的划分则不能用一个标准, 而应具有针对性, 这也是未来需要深入研究的重点内容。此外, 对沉积体系而言, 通常是多期沉积演化的结果, 加之水上与水下的沉积动力存在着较大的差异, 这方面的问题还有很多需要系统攻关, 同样是未来需要关注与攻克的方向。总之, 作者只是提出“物-坡”耦合效应的相关理论基础与探索性研究认识, 希望各位同行批评指正, 并将这种规律与认识进一步完善与发展, 作者相信它将是沉积古地理未来研究的核心与方向。

7 结束语

“物-坡”耦合的观点深化了原有的“源-汇”过程, 从内部因素不同质量颗粒在静止与运动中的受力分析与外部条件古地形斜坡的型式与总体特征地质响应2个角度, 系统分析、推导并模拟了不同碎屑颗粒运动轨迹随着坡型的变化, 由此提出“物-坡”耦合效应的观点。主要认识与观点如下:

1)在Reading的基础上将沉积物划分成5种类型, 并给出了各种粒径的占比范围。同时, 对全球主要沉积斜坡样式进行调研, 结合多年的野外地质研究, 提出线型、下凹型及上凸型3种基本地形斜坡; 依据颗粒模拟计算的结果提出了坡度陡、缓的划分方案及界线, 它们与沉积物类型的分布具有较好的对应关系, 并建议按沉积物的主要类型, 对坡度进行分类, 以体现“源-汇”各区段沉积体系的特色。

2)速度曲线计算结果与Sternberg的结论总体规律一致, 证明了坡型设定与受力分析的合理性。由此可以探讨不同的坡型以及受力背景下沉积物的加积型式。拓展了Sternberg的指数函数结论, 明确了“物-坡”耦合的数理规律, 为后续同行们模拟陆源碎屑沉积物的空间分布提供了理论依据与计算方法。

3)阐明了供源区与汇积区地质观景特征的地形特点与不同级次输送体系(支流与干流)的控制因素与分布规律, 供源区地形斜坡以下凹型为主, 输送体系的表现为支流聚合成干流, 而汇积区多为上凸型, 输送体系表现为干流分散成支流(三角洲称分流河道); 连接两者之间的搬运(主干输送)区通常为线型斜坡, 沉积物主要为过路搬运为主。由此可见沉积物输送体系作用贯穿于“源-汇”的系统全过程中。

4)通过碎屑颗粒的受力分析, 明确指出碎屑物质搬运能量的转换是一定地形坡度下流体搬运过程中速度变化, 体现出不同碎屑颗粒的搬运方式(滚动、跳跃及悬浮)与沉积物输送营力或动力方式的转换(惯性、摩擦及浮力), 不同质量碎屑颗粒的搬运与沉积主要受搬运(水流)能量(流速与流域大小)的控制, 而搬运能量则主要受坡型变化的制约。纵向剖面的速度模拟结果表明, 不同粒径颗粒的运动轨迹随着地形呈抛物线型, 与底床的接触关系由高角度下截逐渐转换为截切转换、高角度下切及低角度下切, 直至平行, 其沉积物相应的由富砾、砂砾、富砂、砂泥直至富泥型的逐渐分布, 且单层厚度逐渐减薄, 各自的分布范围(宽窄)及地形或坡度大小与变化速度的控制, 这种规律反映了顺流加积的主体加积型式。由此说明, 碎屑物质的运动速度决定了其最后的沉积方式。

5)从点-线-面3个维度探讨了“物-坡”耦合效应在垂向序列、剖面加积型式以及平面展布形态的沉积地质响应特征。明确了沉积物输送系统的营力表现形式, 惯性因素为主时坡度陡, 反之坡度缓时摩擦为主, 而流体密度决定了浮力的不同作用机制。高密度流时, 粗粒物质受浮力控制; 而低密度流时, 细粒物质受浮力控制, 同样是坡度的函数。总体是古地形的变化, 控制着流速的能量与变化, 由此影响沉积相带的分布, 而坡度的大小直接控制颗粒的粗细、流体密度、剖面加积型式、平面范围及其形态的分布。总之, 地形坡降与流体密度的变化是造成的沉积物输送3种营力与动力方式相互转换的根本原因, 这就是“物-坡”耦合的相互作用结果。

致谢 感谢本团队的付超博士, 彭子霄、高明轩等博士研究生, 高琦、刘明慷、李苏磊及谢林烨硕士研究生, 他们在文章撰写中参与数理计算、图件绘制以及大量的国内外文献查找核实工作; 长庆油田研究院的高级工程师刘小亮在碎屑颗粒随坡的速度模拟过程, 编制了相关程序。可以说此文章的撰写与成形离不开大家的付出, 在此表示感谢!同时, 也要感谢中国石油大学(北京)朱筱敏教授与中国矿业大学(北京)邵龙义教授提出的宝贵建议!

(责任编辑 郑秀娟)

参考文献
[1] 操应长, 徐琦松, 王健. 2018. 沉积盆地“源-汇”系统研究进展. 地学前缘, 25(4): 116-131.
[Cao Y C, Xu Q S, Wang J. 2018. Progress in “Source-to-Sink”system research. Earth Science Frontiers, 25(4): 116-131] [文内引用:1]
[2] 龚承林, 刘力, 邵大力, 郭荣涛, 朱一杰, 齐昆. 2022. 晚中新世以来孟加拉—尼科巴扇跷跷板式沉积转换及其源-汇成因机制. 地学前缘, 29(4): 25-41.
[Gong C L, Liu L, Shao D L, Guo R T, Zhu Y J, Qi K. 2022. Epositional patterns of the Bengal-Nicobar Fan system since the Late Miocene: seesaw-like stepwise changes and the source-sink model. Earth Science Frontiers, 29(4): 25-41] [文内引用:1]
[3] 韩其为, 何明民. 1979. 单颗泥沙运动力学及统计规律. 力学与实践, 1(4): 35.
[Han Q W, He M M. 1979. Mechanics and statistical law of single sediment movement. Mechanics and Practice, 1(4): 35] [文内引用:1]
[4] 何起祥. 2010. 沉积动力学若干问题的讨论. 海洋地质与第四纪地质, 30(4): 1-10.
[He Q X. 2010. A discussion on sediment dynamics. Marine Geology & Quaternary Geology, 30(4): 1-10] [文内引用:2]
[5] 蒋恕, 王浩, 郭涛, 张如才, 杜晓峰, 张钰莹, 刘恩豪, 王华. 2022. 渤海湾盆地辽东湾坳陷盆中隆起缓坡带重力流沉积形态及其控制因素. 石油与天然气地质, 43(4): 823-832.
[Jiang S, Wang H, Guo T, Zhang R C, Du X F, Zhang Y Y, Liu E H, Wang H. 2022. Geomorphology of gravity flow deposits in the gentle slope zone of intra-basinal high in the Liaodong Bay Depression, Bohai Bay Basin and its controlling factors. Oil & Gas Geology, 43(4): 823-832] [文内引用:1]
[6] 李树芳. 1993. 坡度系数计算法. 建筑工人, (6): 15-16.
[Li S F. 1993. Slope coefficient calculation method. Construction Workers, (6): 15-16] [文内引用:1]
[7] 齐亚林, 赵彦德, 李元昊, 王克. 2018. 泥沙动力学研究方法、技术、进展及沉积学意义. 地球科学前沿(汉斯), 8(1): 7.
[Qi Y L, Zhao Y D, Li Y H, Wang K. 2018. Sedimentology significance from sediment dynamics of research method, technology, progress. Frontiers in Earth Sciences(Hans), 8(1): 7] [文内引用:1]
[8] 邵龙义, 王学天, 李雅楠, 刘炳强. 2019. 深时源-汇系统古地理重建方法评述. 古地理学报, 21(1): 67-81.
[Shao L Y, Wang X T, Li Y N, Liu B Q. 2019. Review on palaeogeographic reconstruction of deep-time source-to-sink systems. Journal of Palaeogeography(Chinese Edition), 21(1): 67-81] [文内引用:1]
[9] 孙龙德, 方朝亮, 李峰, 朱如凯, 何东博. 2010. 中国沉积盆地油气勘探开发实践与沉积学研究进展. 石油勘探与开发, 37(4): 385-396.
[Sun L D, Fang C L, Li F, Zhu R K, He D B. 2010. Petroleum exploration and development practices of sedimentary basins in China and research progress of sedimentology. Petroleum Exploration and Development, 37(4): 385-396] [文内引用:1]
[10] 王成善, 林畅松. 2021. 中国沉积学近十年来的发展现状与趋势. 矿物岩石地球化学通报, 40(6): 1217-1229, 1448-1449.
[Wang C S, Lin C S. 2021. Development status and trend of sedimentology in China in recent ten years. Bulletin of Mineralogy, Petrology and Geochemistry, 40(6): 1217-1229, 1448-1449] [文内引用:1]
[11] 徐长贵, 杜晓峰, 徐伟, 赵梦. 2017. 沉积盆地“源-汇”系统研究新进展. 石油与天然气地质, 38(1): 1-11.
[Xu C G, Du X F, Xu W, Zhao M. 2017. New advances of the “Source-to-Sink”system research in sedimentary basin. Oil & Gas Geology, 38(1): 1-11] [文内引用:1]
[12] 叶连俊, 孙枢, 李继亮. 1988. 中国的沉积学进展与展望. 矿物岩石地球化学通讯, (2): 77-80.
[Ye L J, Sun S, Li J L. 1988. Progress and prospect of sedimentology in China. Bulletin of Mineralogy, Petrology and Geochemistry, (2): 77-80] [文内引用:1]
[13] 于兴河. 2002. 碎屑岩系油气储层沉积学. 北京: 石油工业出版社.
[Yu X H. 2002. Sedimentology of Oil and Gas Reservoirs in Clastic Rocks. Beijing: Petroleum Industry Press] [文内引用:1]
[14] 于兴河, 王德发, 郑浚茂, 孙志华. 1994. 辫状河三角洲砂体特征及砂体展布模型: 内蒙古岱海湖现代三角洲沉积考察. 石油学报, 15(1): 26-37.
[Yu X H, Wang D F, Zheng J M, Sun Z H. 1994. Braided river delta sand body characteristics and sand body distribution model: investigation of modern delta deposits in Daihai Lake, Inner Mongolia. Acta Petrolei Sinica, 15(1): 26-37] [文内引用:1]
[15] 于兴河, 李胜利, 李顺利. 2013. 三角洲沉积的结构: 成因分类与编图方法. 沉积学报, 31(5): 782-797.
[Yu X H, Li S L, Li S L. 2013. Texture-genetic classifications and mapping methods for deltaic deposits. Acta Sedimentologica Sinica, 31(5): 782-797] [文内引用:3]
[16] 于兴河, 李顺利, 谭程鹏, 瞿建华, 张驰, 赵晨帆. 2018. 粗粒沉积及其储层表征的发展历程与热点问题探讨. 古地理学报, 20(5): 713-736.
[Yu X H, Li S L, Tan C P, Qu J H, Zhang C, Zhao C F. 2018. Coarse-grained deposits and their reservoir characterizations: a look back to see forward and hot issues. Journal of Palaeogeography(Chinese Edition), 20(5): 713-736] [文内引用:6]
[17] 朱筱敏, 钟大康, 袁选俊, 张惠良, 朱世发, 孙海涛, 高志勇, 鲜本忠. 2016. 中国含油气盆地沉积地质学进展. 石油勘探与开发, 43(5): 820-829.
[Zhu X M, Zhong D K, Yuan X J, Zhang H L, Zhu S F, Sun H T, Gao Z Y, Xian B Z. 2016. Development of sedimentary geology of petroliferous basins in China. Petroleum Exploration and Development, 43(5): 820-829] [文内引用:1]
[18] Alberto R, Sergio A, Eduardo G. 2018. Quantifying roundness of detrital minerals by image analysis: sediment transport, shape effects, and provenance implications. Journal of Sedimentary Research, 88(2): 276-289. doi: https://doi.org/10.2110/jsr.2018.12. [文内引用:1]
[19] Allen P A. 2008. Time scales of tectonic land scapes and their sediment routing systems. Geological Society, London, Special Publications, 296(1): 7-28. [文内引用:1]
[20] Allen P A. 2017. Sediment Routing Systems: The Fate of Sediment from Source-to-Sink. Cambridge University Press. [文内引用:6]
[21] Anderton R. 1985. Clastic facies models and facies analysis. Geological Society, London, Special Publications, 18(1): 31-47. [文内引用:1]
[22] Armitage J J, Duller R A, Whittaker A C, Allen P A. 2011. Transformation of tectonic and climatic signals from source to sedimentary archive. Nature Geoscience, 4(4): 231-235. [文内引用:1]
[23] Ashton A D, Giosan L. 2011. Wave-angle control of delta evolution. Geophysical Research Letters, 38(13): 1-6. [文内引用:1]
[24] Ashworth P J, Ferguson R I. 1989. Size-selective entrainment of bed load in gravel bed streams. Water Resources Research, 25(4): 627-634. [文内引用:1]
[25] Bagnold R A. 1986. Transport of solids by natural water flow: evidence for a worldwide correlation. Proceedings of the Royal Society of London. Mathematical and Physical Sciences, 405(1829): 369-374. [文内引用:1]
[26] Bentley Sr S J, Blum M D, Maloney J, Pond L, Paulsell R. 2016. The Mississippi River source-to-sink system: perspectives on tectonic, climatic, and anthropogenic influences, Miocene to Anthropocene. Earth-Science Reviews, 153: 139-174. [文内引用:1]
[27] Bhattacharya J P, Copeland P, Lawton T F, Holbrook J. 2016. Estimation of source area, river paleo-discharge, paleoslope, and sediment budgets of linked deep-time depositional systems and implications for hydrocarbon potential. Earth-Science Reviews, 153: 77-110. [文内引用:2]
[28] Boudet L, Sabatier F, Radakovitch O. 2017. Modelling of sediment transport pattern in the mouth of the Rhone delta: role of storm and flood events. Estuarine, Coastal and Shelf Science, 198: 568-582. [文内引用:1]
[29] Brenna A, Marchi L, Borga M, Ghinassi M, Zaramella M, Surian N. 2021. Sediment-water flows in mountain catchments: insights into transport mechanisms as responses to high-magnitude hydrological events. Journal of Hydrology, 602: 126716. [文内引用:1]
[30] Bull W B. 1977. The alluvial-fan environment. Progress in Physical Geography, 1(2): 222-270. [文内引用:1]
[31] Cai X Y, Zhu R. 2011. Cretaceous sand body characters at shallow-water lake delta front and the sedimentary dynamic process analysis in Songliao Basin, China. Acta Geologica Sinica-English Edition, 85(6): 1478-1494. [文内引用:1]
[32] Caracciolo L. 2020. Sediment generation and sediment routing systems from a quantitative provenance analysis perspective: review, application and future development. Earth-Science Reviews, 209: 103226. [文内引用:1]
[33] Catuneanu O. 2006. Principles of Sequence Stratigraphy. Trevor Elliott. [文内引用:1]
[34] Catuneanu O, Abreu V, Bhattacharya J P, Blum M D, Dalrymple R W, Eriksson P G, Winker C. 2009. Towards the stand ardization of sequence stratigraphy. Earth-Science Reviews, 92(1-2): 1-33. [文内引用:1]
[35] Church M. 2006. Bed material transport and the morphology of alluvial river channels. Annual Review of Earth Planetary Sciences, 34: 325-354. [文内引用:1]
[36] Cogan J, Gratchev I. 2019. A study on the effect of rainfall and slope characteristics on land slide initiation by means of flume tests. Land slides, 16(12): 2369-2379. [文内引用:1]
[37] Cross T. 1988. Controls on coal distribution in transgressive-regressive cycles, Upper Cretaceous, Western Interior, USA. In: Wilgus C K, Hastings B S, Posamentier H, van Wagoner J, Ross C A S, Kendal C G St C(eds). Sea-level changes: an integrated approach. Society for Sedimentary Geology, Special Publication, 42: 371-389. https://doi.org/10.2110/pec.88.01.0371. [文内引用:1]
[38] Dade W B, Friend P F. 1998. Grain-size, sediment-transport regime, and channel slope in alluvial rivers. The Journal of Geology, 106(6): 661-676. [文内引用:1]
[39] Emery D, Myers K. 2009. Sequence Stratigraphy. USA: John Wiley & Sons, 11-45. [文内引用:1]
[40] Fanning J T. 1877. A Practical Treatise on Water-Supply Engineering: Relating to the Hydrology, Hydrodynamics, and Practical Construction of Water-Works, in North America. With Numerous Tables and Illustrations. USA: Wagoner Nostrand , 1-714. [文内引用:2]
[41] Ferrer-Boix C, Martín-Vide J P, Parker G. 2015. Sorting of a sand -gravel mixture in a Gilbert-type delta. Sedimentology, 62(5): 1446-1465. [文内引用:1]
[42] Fryirs K A, Brierley G J. 2012. Geomorphic Analysis of River Systems: An Approach to Reading the Land scape. USA, John Wiley & Sons. [文内引用:1]
[43] Geleynse N, Storms J E, Walstra D J R, Jagers H A, Wang Z B, Stive M J. 2011. Controls on river delta formation: insights from numerical modelling. Earth and Planetary Science Letters, 302(1-2): 217-226. [文内引用:1]
[44] Harvey A M, Mather A E, Stokes M. 2005. Alluvial fans: geomorphology, sedimentology, dynamics. Geological Society of London, Special Publications, 251: 1-7. [文内引用:1]
[45] Hayes M O. 1980. General morphology and sediment patterns in tidal inlets. Sedimentary Geology, 26(1-3): 139-156. [文内引用:1]
[46] Hoy R G, Ridgway K D. 2003. Sedimentology and sequence stratigraphy of fan-delta and river-delta deposystems, Pennsylvanian Minturn Formation, Colorado. AAPG Bulletin, 87(7): 1169-1191. [文内引用:1]
[47] Kenyon P M, Turcotte D L. 1985. Morphology of a delta prograding by bulk sediment transport. Geological Society of America Bulletin, 96(11): 1457-1465. [文内引用:1]
[48] Lajeunesse E, Malverti L, Charru F. 2010. Bed load transport in turbulent flow at the grain scale: experiments and modeling. Journal of Geophysical Research: Earth Surface, 115(F04001): 1-16. [文内引用:1]
[49] Lin C S, Xia Q L, Shi H S, Zhou X H. 2015. Geomorphological evolution, source to sink system and basin analysis. Earth Science Frontiers, 22(1): 9-20. [文内引用:1]
[50] Long D G F. 2021. Trickling down the paleoslope: an empirical approach to paleohydrology. Earth-Science Reviews, 220: 103740. [文内引用:1]
[51] McLaren P, Bowles D. 1985. The effects of sediment transport on grain-size distributions. Journal of Sedimentary Research, 55: 457-470. [文内引用:1]
[52] McLaren P, Hill S H, Bowles D. 2007. Deriving transport pathways in a sediment trend analysis(STA). Sedimentary Geology, 202(3): 489-498. [文内引用:2]
[53] Nemec W, Steel R J. 1984. Alluvial and coastal conglomerates: their significant features and some comments on gravelly mass-flow deposits. In: Sedimentology of Gravel and Conglomerates. Canada: Canadian Society of Petroleum Geologists, 1-31. [文内引用:1]
[54] Nemec W, Steel R J, Poreebski S J, Spinnangr Å. 1984. Domba Conglomerate, Devonian, Norway: process and lateral variability in a mass flow-dominated, lacustrine fan-delta. In: Canadian Society of Petroleum Geologists(ed). Sedimentology of Gravels and Conglomerates. Calgary Alta, Canada: Canadian Society of Petroleum Geologists, 295-320. [文内引用:1]
[55] Nichols G. 2009. Sedimentology and Stratigraphy. USA: John Wiley & Sons, 5-35. [文内引用:1]
[56] Parsons D R, Best J L, Lane S N, Orfeo O, Hardy R J, Kostaschuk R. 2010. Form roughness and the absence of secondary flow in a large confluence-diffluence, Rio Paraná, Argentina. Earth Surface Processes & Land forms, 32(1): 155-162. [文内引用:1]
[57] Patruno S, Hampson G J, Jackson C A L, Dreyer T. 2015. Clinoform geometry, geomorphology, facies character and stratigraphic architecture of a sand -rich subaqueous delta: Jurassic Sognefjord Formation, offshore Norway. Sedimentology, 62(1): 350-388. [文内引用:1]
[58] Prior D B, Doyle E H, Kaluza M J. 1989. Evidence for sediment eruption on deep sea floor, Gulf of Mexico. Science, 243(4890): 517-519. [文内引用:1]
[59] Reading H G, Richards M. 1994. Turbidite systems in deep-water basin margins classified by grain size and feeder system. AAPG Bulletin, 78(5): 792-822. [文内引用:5]
[60] Reading H G. 2009. Sedimentary Environments: Processes, Facies and Stratigraphy. USA: John Wiley & Sons, 5-25. [文内引用:1]
[61] Reitz M D, Jerolmack D J. 2012. Experimental alluvial fan evolution: channel dynamics, slope controls, and shoreline growth. Journal of Geophysical Research: Earth Surface, 117(F02021): 1-19. [文内引用:1]
[62] Shanmugam G. 2013. New perspectives on deep-water sand stones: implications. Petroleum Exploration and Development, 40(3): 294-301. [文内引用:1]
[63] Sømme T O, Jackson C A L. 2013. Source-to-sink analysis of ancient sedimentary systems using a subsurface case study from the Møre-Trøndelag area of southern Norway: part 2-sediment dispersal and forcing mechanisms. Basin Research, 25(5): 512-531. [文内引用:2]
[64] Sternberg H. 1875. Untersuchungen uber Langen-und Querprofil geschiebefuhrender Flusse. Zeitshrift fur Bauwesen, 25: 483-506. [文内引用:2]
[65] Stokes G G. 1851. On the effect of the internal friction of fluids on the motion of pendulums. Oxford England : University Press, 8-106. [文内引用:1]
[66] Trask P D. 1959. Effect of grain size on strength of mixtures of clay, sand , and water. Geological Society of America Bulletin, 70(5): 569-580. [文内引用:1]
[67] Udden J A. 1914. Mechanical composition of clastic sediments. Geological Society of America Bulletin, 25: 655-744. [文内引用:1]
[68] Vail P R, Mitchum Jr R M, Thompson III S. 1977. Seismic stratigraphy and global changes of sea level: Part 3. Relative changes of sea level from Coastal Onlap: section 2. Application of Seismic Reflection Configuration to Stratigrapic Interpretation: 63-81. [文内引用:1]
[69] Visher G S. 1969. Grain size distributions and depositional processes. Journal of Sedimentary Research, 39(3): 1074-1106. [文内引用:1]
[70] Wentworth C K. 1922. A scale of grade and class terms for clastic sediments. The Journal of Geology, 30: 377-392. [文内引用:1]
[71] Wilcock P R, Crowe J C. 2003. Surface-based transport model for mixed-size sediment. Journal of Hydraulic Engineering, 129(2): 120-128. [文内引用:1]
[72] Wood A. 1942. The development of hillside slopes. Proceedings of the Geologists' Association, 53(3-4): 128-IN3. [文内引用:3]
[73] Yu X H, Li S L, Chen B T, Tan C P, Xie J, Hu X N. 2012. Interaction between downslope and along slope processes on the margins of Daihai lake, north China: implication for deltaic sedimentation models of lacustrine rift basin. Acta Geologica Sinica-English Edition, 86(4): 932-948. [文内引用:1]
[74] Yu X H, Li S L, Tan C P, Xie J, Chen B T, Yang F, Liu L. 2013. The response of deltaic systems to climatic and hydrological changes in Daihai Lake rift basin, Inner Mongolia, northern China. Journal of Palaeogeography, 2(1): 41-55. [文内引用:1]