王俊辉, 鲜本忠. (2023). 冲积河流平衡的再认识* [J]. 古地理学报, 25(5): 1011-1031.
WANG Junhui, XIAN Benzhong. (2023). Revisiting the concept of alluvial river grade[J]. Journal Of Palaeogeography, 25(5): 1011-1031.   
Doi: 10.7605/gdlxb.2023.05.085
Permissions
Copyright©2023, 《古地理学报》编辑部
版权所有.《古地理学报》编辑部
冲积河流平衡的再认识*
王俊辉1,2, 鲜本忠1,2
1 油气资源与工程全国重点实验室,中国石油大学(北京),北京 102249
2 中国石油大学(北京)地球科学学院,北京 102249

第一作者简介 王俊辉,男,1988年生,中国石油大学(北京)地球科学学院副教授、博士生导师,主要从事沉积学研究。E-mail: wangjunhui@cup.edu.cn。

收稿日期:2023-01-18 修回日期:2023-04-26
基金资助:*国家自然科学基金项目(编号: 42172108)和中国石油大学(北京)科研基金项目(编号: 2462020BJRC002,2462020YXZZ020)联合资助
摘要

河流平衡是指河流在输送沉积物的过程中达到了无净沉积、无净侵蚀、沉积物过路不留的平衡状态。它代表了沉积物加积与侵蚀的临界状态,因此是地貌学、地质学和地层学的基本概念。传统观点认为,在基准面、物源供给等外部条件保持不变的情况下,河流总会自发地向理论平衡剖面去逼近,最终达到平衡状态。这种传统观点适用于河流的局部平衡,并不适用于冲积河流的整体平衡。这是因为传统观点并未充分考虑源汇系统尺度下的冲积河流整体具有自由边界的特性(河流上游与下游端可以自由延长)。如在冲积河流系统的末端,三角洲的进积使得河流剖面延长,这一过程必然伴随着河流的加积。这表明在自由边界条件下,冲积河流实现整体平衡的必要条件是基准面下降,而非稳定。物理与数值模拟实验进一步证明了冲积河流达到系统整体平衡的 3种情形: ( 1)强制平衡。发生于河流末端无法延长的固定边界条件下(如蓄水盆地坡度很陡、水深很大等情形),河流平衡于稳定基准面。( 2)自成因平衡。发生于自由边界条件、河流剖面的坡度与河流末端下超面坡度(盆地坡度)相等的条件下,河流平衡于稳定下降的基准面。( 3)他成因平衡。发生于自由边界条件、河流剖面的坡度小于河流末端下超面坡度的条件下,河流平衡于以特定方式减速下降的基准面。注重地层叠置过程的成因地层学理论应当充分考虑这 3种河流平衡的方式,才能更为准确解释地层叠置的成因。

关键词: 河流平衡; 基准面; 自成因与他成因; 层序地层学; 成因地层学
中图分类号:P532 文献标志码:A 文章编号:1671-1505(2023)05-1011-21
Revisiting the concept of alluvial river grade
WANG Junhui1,2, XIAN Benzhong1,2
1 National Key Laboratory of Petroleum Resources and Engineering,China University of Petroleum(Beijing),Beijing 102249,China
2 College of Geosciences,China University of Petroleum(Beijing),Beijing 102249,China

About the first author WANG Junhui,born in 1988,is an associate professor from China University of Petroleum(Beijing). He is mainly engaged in sedimentology. E-mail: wangjunhui@cup.edu.cn.

Fund:Co-funded by the National Natural Science Foundation of China(No.42172108)and Science Foundation of China University of Petroleum(Beijing)(Nos. 2462020BJRC002,2462020YXZZ020)
Abstract

Grade refers to the state of a river where sediment is conveyed without net deposition or net erosion but completely bypassed through the river. The concept of grade is fundamental to geomorphology,geology and stratigraphy,because it represents the critical condition between river aggradation and degradation. According to conventional views,rivers will spontaneously approach the theoretical graded profile and finally reach it,given constant external forcings such as stable base level and steady sediment supply. The conventional notion of grade is valid for local scale of the alluvial system,but not for system scale of the whole alluvial system from a source-to-sink perspective. This is because the conventional notion seldom considers the free boundary condition of the alluvial system( i.e.,the upper and lower boundary of the alluvial system can move freely). For example,extension of the alluvial system by delta progradation at the downstream end of the river is inevitably accompanied by alluvial aggradation. This indicates that in moving boundary conditions,the necessary condition for the alluvial river to attain the state of grade at system scale is base level fall rather than base level standstill. Physical and numerical experiments further verified that the alluvial river can reach system-scale grade by three ways. (1)Forced grade,which can be realized in fixed downstream boundary conditions,for example,the downstream end of the alluvial river cannot extend freely by extreme deep basin water depth. In this case,the alluvial river grades to stationary base level. (2)Autogenic grade,which is realized in full moving boundary conditions and the basin floor slope equals that of the alluvial system. In this case,constant rate of base level fall is necessary. (3)Allogenic grade,which is realized in full moving boundary conditions and the basin floor slope is steeper than that of the alluvial system. In this case,slowing down of the base level fall in a particular pattern is necessary. Genetic stratigraphy which highlights the stacking process of strata should fully take the three ways of grade into account,by which the interpretation of stacking of strata will be clearer.

Key words: alluvial grade; base level; autogenesis and allogenesis; sequence stratigraphy; genetic stratigraphy
1 概述

河流是沟通源-汇系统的重要纽带, 由上游的基岩段和下游的冲积段组成。河流平衡是指在冲积段, 河流在搬运沉积物的过程中, 从上游供给的沉积物数量与自下游流出的数量相当, 沉积作用与侵蚀作用达到动态平衡, 在河流剖面中既不发生净沉积作用、也不发生净侵蚀作用。因为它表示了地层加积与侵蚀的临界状态, 是冲积体系地貌学、地质学、地层学极其重要的基础概念。这一点通过了解河流平衡的英文表达可以直观地体会出来。表达河流平衡的英文单词是“ grade” 。该单词作为日常单词含义众多, 其中有“ 标准” 之意, 在工程学中有“ 地平面” 、“ 参考水准面” 之意, 在地球科学领域指地貌的“ 均夷状态” 、“ 夷平状态” 。1902年, 在“ grade” 已被学者多次用于河流沉积的背景下, 美国地理学家、地质学家和气象学家William Morris Davis提倡用“ grade” 指作“ 河流侵蚀与沉积的平衡” 之意, 这一用法随后被传播开来。在地层学中, 围绕“ grade” , 进一步派生出“ aggrade” (加积)、“ degrade” (侵蚀)、“ prograde” (进积)、“ retrograde” (退积)(Davis, 1902; Catuneanu, 2019), 代表了地层叠置的4种基本过程。

河流平衡尽管在概念上容易理解, 但对河流达到平衡的条件的认识并不清楚。传统观点是通过假想河流存在一条理论的纵剖面— — 平衡剖面来理解河流的平衡(Mackin, 1948; Bolla Pittaluga et al., 2014; Blom et al., 2016): 在平衡剖面上, 河流搬运沉积物的能力与上游供给沉积物的数量恰好相当; 而大部分河流剖面实际上是偏离于平衡剖面的, 河流会通过侵蚀作用(实际剖面高于平衡剖面)或堆积作用(实际剖面低于平衡剖面)不断向理论平衡剖面逼近。传统观点也认为, 假定所有的外部条件保持不变, 平衡将是河流达到的最终状态(Kesseli, 1941; Mackin, 1948; Chang, 1986; Posamentier and Vail, 1988; Schumm, 1993; Wescott, 1993)。

近年, 基于正演的模拟和理论研究对传统河流平衡的观点提出了质疑, 指出传统观点对于理解冲积河流在局部的平衡可能有效(Bolla Pittaluga et al., 2014; 邓彩云等, 2015), 但在考虑冲积河流全河段的平衡时存在缺陷(Muto and Swenson, 2005, 2006a; Bijkerk et al., 2016)。随着源汇体系(Allen, 2008; Sø mme et al., 2009; 林畅松等, 2015; 徐长贵等, 2017; 朱红涛等, 2017; 操应长等, 2018; 邵龙义等, 2019; 朱筱敏等, 2019; 陈星渝等, 2023)、以及以层序地层学(Posamentier et al., 1988; Catuneanu, 2006; 纪友亮和周勇, 2020; 龚承林等, 2021; 朱筱敏, 2023)、过程地层学(Allen and Allen, 2005; Karamitopoulos et al., 2021)、自成因地层学(Muto et al., 2007; Muto et al., 2016b)等为代表的成因地层学的兴起, 在大尺度上研究河流的侵蚀、加积与平衡状态逐渐深入, 对河流平衡、尤其是冲积河流全河段平衡的正确认识显得尤为重要。这是因为冲积河流的整体平衡涉及地质学、地层学的理论基础, 不少相关的理论和概念建立在河流平衡的基础之上。例如, 层序地层学的基础理论和概念如A/S(A为可容空间变化速率、S为沉积物供给速率)、基准面等均建立在对冲积河流整体平衡的理解上(Jervey, 1988; Posamentier and Vail, 1988; Shanley and McCabe, 1994)。

作者首先回顾河流平衡的概念, 解释冲积河流平衡的必要条件及表现特征, 通过梳理河流达到平衡的3种情况, 阐述对河流平衡的新的理解。文中讨论的对象是源汇尺度下的冲积河流系统, 所讨论的河流平衡是指冲积河流全河段的平衡(从冲积区的上游端开始至海岸线, 与源汇的尺度相当, 但不包括基岩区)。

2 河流平衡的含义与传统认识
2.1 河流平衡与平衡剖面

2.1.1 河流平衡

河流平衡(grade)的概念可以追溯到19世纪(Gilbert, 1877), 随后被多次使用(Davis, 1902; Barell, 1912; Kesseli, 1941), 直至20世纪40年代, Mackin(1948)对其做了广为接受的定义后, 被采用至今: 在持续稳定的水流量和沉积物供给以及河道特征保持稳定的条件下, 河流经过一定时间的自我调整, 河道的坡度将使得河水的流速恰好足够搬运自上游流入的全部沉积物(A graded stream is one in which, over a period of years, slope is delicately adjusted to provide, with available discharge and with prevailing channel characteristics, just the velocity required for the transportation of the load supplied from the drainage basin)。

河流达到平衡状态后, 河道中既不发生净沉积、也不发生净侵蚀, 达到侵蚀与沉积的平衡。这是一种动态平衡: 对于某一河段在某一时间段内, 尽管有沉积物的流入和流出, 但流入与流出的沉积物数量相当, 在该时段内存在于该河段中的沉积物总量保持不变。根据上述河流平衡的定义和理解, 从时间上讲, 河流的平衡只是暂时的。这是因为, 外部条件如上游来水流量、上游来砂流量、河床坡度、海平面等很难保持持续稳定, 即使河流达到平衡, 如果这些外界条件发生了改变(而这是经常且普遍发生的), 河流的平衡将被打破, 并将向新的平衡演变。此外, 从空间上来看, 河流平衡的定义也并没有强调河流在全河段平衡, 而更多地关注某一河段的平衡。

2.1.2 河流平衡剖面与基准面

在理论上, 河流也可能达到全河段的平衡, 这时, 河流的纵剖面称作平衡剖面(Mackin, 1948; Bolla Pittaluga et al., 2014; Blom et al., 2016)。由于河流自上游到下游, 众多自然因素(气候、水文、岩性、地壳运动等)均可能不同, 这些因素都能影响河床纵剖面发展, 从而控制河流平衡剖面。受多种因素影响, 如分异作用使得沉积物自上游至下游粒度逐渐变细(Paola et al., 1992; Blom et al., 2016; Nones et al., 2019; 马字发等, 2022), 支流的汇入使得下游流量增大(Sinha and Parker, 1996), 河道沿程宽度的变化(Li et al., 2014; Ferrer-Boix et al., 2016)等, 河流平衡剖面通常认为是一条下凹的曲线(图 1)。

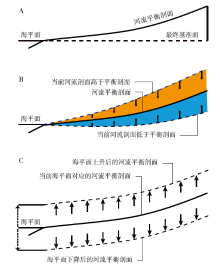图 1 河流平衡的传统认识
A— 河流平衡剖面表现为一条上游陡、下游缓的下凹曲线。海平面对应于最终基准面(或称侵蚀基准面、地貌基准面); B— 如果实际河流的剖面低于平衡剖面, 河流将通过加积作用向其逼近; 反之, 河流将通过侵蚀作用向其逼近; C— 基准面上升将带动平衡剖面上升, 河床加积抬升; 基准面下降带动平衡剖面下降, 河床遭受侵蚀(改自Muto and Swenson, 2006b)Fig.1 Conventional view on alluvial grade

与平衡剖面相关的另一个概念是基准面。在地层学中, 基准面是控制沉积与侵蚀作用的临界面。从定义上看, 其与平衡剖面有相似之处。但在实际工作中, 地质学工作者对基准面的理解不尽相同, 如: 有的将海平面作为基准面(均夷作用的终极基准面, 也称作“ 侵蚀基准面” 或“ 地貌基准面” , Bates and Jackson, 1987; 邬金华等, 1997); 有的将陆地与海洋(或湖泊)分别对待, 将海平面作为洋(或湖)区的基准面、将河流平衡剖面作为陆区的基准面(Catuneanu, 2019); 也有将“ 地层基准面” 抽象作存在于地球表面任何位置的、区分侵蚀与沉积作用的、相对于地球表面波状起伏的连续抽象曲面(Wheeler, 1964; Shanley and McCabe, 1994; Cross and Homewood, 1997; Cross and Lessenger, 1998; 邓宏文等, 2000; 王嗣敏和刘招君, 2001)。这些对基准面的不同理解在各自的语义背景中都是适用的, 文中不予以评述。在文中, 将基准面等同于河流入海(湖)口的水平面(海平面或湖平面), 与Schumm对基准面词义的剖析一致(Schumm, 1993), 与“ 侵蚀基准面” (Bates and Jackson, 1987)相当(图 1-A)。经典层序地层学也多采用这种方案(Posamentier and Vail, 1988; Posamentier and Allen, 1999)。在这种背景下, 海/湖平面(或基准面)升降对河流体系的沉积与侵蚀作用的控制更便于讨论, 因为基准面的上升与下降, 将带动基准面与河流平衡剖面的交点(均衡点)上下运动, 从而可能(并非一定)引起河流平衡剖面的变化, 以此控制沉积或者侵蚀作用的发生。

2.2 关于河流平衡的传统推论

2.2.1 平衡是河流试图达到的最终状态

普遍认为, 河流具有自我调节的机能。当外界条件保持稳定的状态下, 河流总是通过调整相关参数, 如河床坡度、截面形态、河床沉积物的粒径等, 自发性地向平衡状态发展(Chang, 1986; Schumm, 1993; Wescott, 1993)。这些外界条件包括但不限于大地构造背景、气候条件、沉积物供给量、水流量、相对海平面等。当这些外界条件保持稳定不变, 河流的平衡剖面也默认是固定的。如果实际河流的剖面低于平衡剖面, 河流将通过加积作用向其逼近; 如果实际河流的剖面高于平衡剖面, 河流将通过侵蚀作用向其逼近(图 1-B)。当河流达到了平衡状态, 则认为河流达到了成熟期或老年期(Davis, 1902; Kesseli, 1941; Schumm, 1993), 即平衡是河流试图达到的最终状态。

2.2.2 河流平衡于稳定的基准面

假设气候条件、沉积物供给量、水流量等外部条件保持不变, 而只考虑河流平衡与基准面的关系, 则稳定的基准面是河流实现平衡的必要条件(Davis, 1902; Green, 1936; Kesseli, 1941; Leopold and Bull, 1979; Posamentier and Vail, 1988; Thorne and Swift, 1991; Johnson and Beaumont, 1995; Holbrook et al., 2006)。这种认识的一个推论是, 当基准面上升, 将带动平衡剖面上升, 为达到最新的平衡剖面河床将加积抬升, 基准面上升相当于创造了可容空间; 基准面下降, 将带动平衡剖面下降, 为达到最新的平衡剖面河流倾向于侵蚀下切, 相当于可容空间遭到破坏(Jervey, 1988; Posamentier et al. 1988; Posamentier and Vail, 1988; Van Wagoner et al., 1990; Shanley and McCabe, 1994; Posamentier and Allen, 1999; Catuneanu et al., 2009)(图 1-C)。

这一推论进一步构成了层序地层学的理论基础之一, 即A/S理论(Jervey, 1988; Shanley and McCabe, 1994)。对于可容空间增加(A> 0), 如果自上游供给而来的沉积物在补偿了新增的可容空间之后仍有剩余, 则发生海退进积(即A/S< 1); 如果上游供给而来的沉积物恰好补偿新增的可容空间, 则表现为持续加积(即A/S=1); 如果上游供给而来的沉积物不足以补偿新增的可容空间, 则表现为海侵退积(即A/S> 1)。对于可容空间零增加, 河流最终将达到平衡状态。对于可容空间减少(A< 0)的情况, 河流侵蚀下切。

3 冲积河流全河段的平衡

近年的理论研究与模拟实验对上述传统认识进行了补充和修正。其中一个主要的认识是: 在河流末端可以自由进积的情况下, 河流不是平衡于稳定的基准面, 而是下降的基准面(Nummedal et al., 1993; Leeder and Stewart, 1996; Muto and Swenson, 2005, 2006a, 2006b)。这是因为, 在稳定的基准面条件下, 河口处沉积作用的发生必然使得河流及其平衡剖面延长, 这就不可避免地使平衡剖面抬升(图 2)。因此, 在稳定的基准面条件下, 河流必然发生持续的加积作用。传统的“ 河流平衡于稳定基准面” 的认识, 忽略了冲积河流系统伴随三角洲进积作用的发生必然使其下游边界延长(Muto and Steel, 2000; Swenson et al., 2000, 2005; Muto and Swenson, 2005; Bijkerk et al., 2016), 即冲积河流系统的边界具有自由移动的特征。

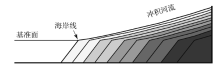图 2 河流末端进积必然引起河流剖面延长和河床加积, 冲积河流无法达到平衡(据Muto and Swenson, 2005; Bijkerk et al., 2016; 有修改)Fig.2 Progradation inevitably results in extension of the longitudinal river profile and riverbed aggradation, and thus alluvial river cannot achieve grade(modified from Muto and Swenson, 2005; Bijkerk et al., 2016)

3.1 冲积河流系统的特点— — 自由边界

从物源区到入海口, 河流由上游的基岩段和下游的冲积段组成。从河流平衡的定义来看, 河流的平衡是指冲积河流(即下游段)的平衡, 而非基岩段(上游段)的平衡, 因为只有冲积河流才涉及河水与河底的沉积物交换问题。

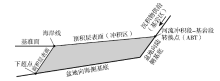
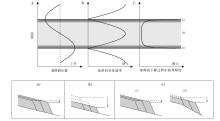
在顺物源方向的二维剖面上, 冲积河流系统主要由3个边界限定, 它们在侵蚀、沉积作用下具有自由移动的特点。这3个边界是: (1)在上游方向, 冲积河流的起点在与基岩河流相接处, 即河流的冲积段— 基岩段转换点(alluvial-bedrock transition, 简称ABT; 相当于上超点); (2)在下游方向, 以基准面为界, 沉积物流出河流系统, 即海岸线(shoreline); (3)多数情况下冲积体系末端发育三角洲, 三角洲前积层的下超点可抽象为整个河流— 三角洲冲积体系的终点。这3个边界具有自由移动的特点, 称作自由边界(图 3)。

图 3 河流— 三角洲体系自由边界示意图(注意河流的冲积段— 基岩段转换点(ABT)、海岸线、下超点在河流— 三角洲体系的发育过程中是可以自由移动的)Fig.3 Schematic of the free boundary condition of the fluvial-deltaic system(Note that the alluvial-basement transition, shoreline, and delta toe are moving boundaries during the development of the fluvial-deltaic system)

地层的4种基本响应方式(加积、侵蚀、进积、退积)均可以通过自由边界的移动特征反映出来。例如, ABT沿基岩河床向上游方向移动, 表明冲积河流发生加积, 向下游方向移动, 表明河流发生侵蚀作用; 海岸线垂直向上运动, 代表加积作用, 垂直向下移动, 代表侵蚀作用, 水平向前(海洋方向)运动, 表明进积(海退), 水平向后(陆地方向)运动, 表明退积(海侵); 下超点向前移动表明前积和下超, 向后移动则表明退积。

3.2 冲积河流全河段平衡的特征

对于全河段达到平衡的冲积河流, 主要有以下3个特点:

1)沉积物过路不留, 河床剖面稳定不变。由于没有净沉积作用和净侵蚀作用的发生, 整个河床的加积速率为0(即Ragg=0; Ragg> 0表示加积, Ragg< 0表示下切侵蚀), 河床剖面没有垂直向上或向下的变化。

2)由于河床剖面没有上升和下降, 与此相关的另外一个显著的特征就是ABT的位置固定不变。

3)河流达到平衡, 也意味着河水中的沉积物数量不再变化, 沉积物流量(qs)与河水流量(qw)之比也成为定值(qs/qw为定值)。另一方面, qs/qw又决定了沉积物扩散和河床坡度。因此, 对于河流平衡, 其剖面有可能表现为一条直线(Parker and Anderson, 1977), 而非传统观点认为的总是呈现向下凹的曲面。

需要说明的是, 冲积河流达到平衡后, 并不意味着侵蚀或沉积作用不再发生。河水中的沉积物仍然可以与河床的沉积物进行物质交换。从空间上来看, 河流可能在局地发生侵蚀(或加积), 但这种局部的侵蚀(或加积)将在另一处通过加积(或侵蚀)得以补偿, 只要在整个冲积河流系统内, 侵蚀与加积达到平衡即可。同理, 从时间上来看, 河流可能发生短暂的侵蚀(或加积), 只要这种侵蚀(或加积)在另一时刻通过加积(或侵蚀)得以补偿, 从而在适当长的时间内观察(取决于研究的时间尺度), 侵蚀与加积达到平衡即可。

以下关于河流的平衡, 主要探讨河流平衡与基准面两者的关系。所有其他来自上游的外部条件, 如沉积物供给、沉积物分配、水流量、气候变化等对此过程的影响均不考虑在内, 即假定这些其他的外部条件均保持稳定。将基准面与其他控制因素分开讨论, 能够有效讨论基准面与河流平衡的关系。

4 冲积河流平衡的3种方式
4.1 强制平衡

只有忽略河流下游端点自由边界的属性, 传统的“ 河流平衡于稳定基准面” 的观点才能成立。在一些特殊的背景下, 自上游供给而来的沉积物, 一旦到达河流的末端便离开了河流系统。类似的情形包括但不限于: 河道注入水深无穷大的蓄水盆地; 蓄水盆地的波浪、潮汐、沿岸流能够有效地疏浚河口区沉积物等。在这种情况下, 尽管上游沉积物持续供给, 但河流末端的位置保持固定不变, 使得河流无法延长。因此, 河流末端不会发生净沉积或净侵蚀作用, 而仅仅是沉积物的流出。当自河流末端流出的沉积物与自上游而来的沉积物数量相当, 河流便达到了平衡。这种通过强制性地抑制河床的延长而达到的河流平衡, 称作强制平衡(forced grade; Muto et al., 2016a)。

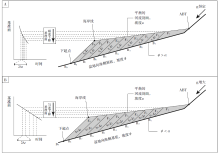
强制平衡在实验室很容易实现。Parker和Anderson(1977)曾提出这样的模型: 在一个单斜的二维水槽中, 放置一个挡板, 起到堰的作用(图 4-A)。在堰的上游区域, 形成一个水位由堰高决定的蓄水体; 携砂水流自上游供给。携砂水流到达蓄水体后, 便开始形成三角洲(图 4-A; 在堰的右侧, 前积层发育, 表明沉积体系末端达到堰之前处于三角洲的发育阶段)。在持续的物源供给条件下, 岸线持续向堰的方向进积, 在同时发生的加积作用下, ABT向上游方向迁移, 这一过程持续至蓄水体被沉积物填满、岸线抵达堰顶, 前积层随之消失, 沉积体系演变为单一的河流体系。此后, 到达岸线的沉积物无法继续沉积在由堰限定的冲积区域, 而是越过堰, 流出冲积区, 进积作用停止; 另一方面, 没有抵达堰顶的沉积物使得加积作用继续进行, ABT持续向上游方向迁移(上超)。在这种作用下, 河流不断改变其坡度, 直至所有自上游流入冲积体系的沉积物全部自堰顶流出, 加积作用停止, ABT也不再迁移, 河流达到平衡状态。此时, 河流的剖面表现为一条直线, 在不改变物源供给(供砂量、供水量)的条件下将维持下去而不再改变。上述二维模型也在水槽实验中得到了验证(图 4-B)。

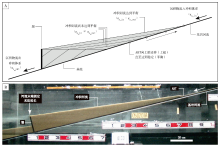图 4 二维强制平衡模型与水槽实验(据Parker and Anderson, 1977; Muto and Swenson, 2005, 2006b)
A— 河流末端到达堰顶之前, 表现为加积。河流末端到达堰顶后无法继续延长, 所有自上游供给的沉积物全部经堰顶流出冲积体系, 冲积河流经过一段时间的加积后达到平衡(ABT继续向上游方向移动一段距离后保持静止)(Parker and Anderson, 1977); B— 二维水槽实验实现强制平衡(Muto and Swenson, 2006b)。与传统认识中河流的平衡剖面表现为下凹的曲线不同, 该实验实现的河流平衡剖面表现为一条直线。ABT: 河流的冲积段— 基岩段转换点Fig.4 Illustration of forced grade model and flume experiment in 2-dimension(after Parker and Anderson, 1977; Muto and Swenson, 2005, 2006b)

在上述模型中, 由于堰的存在, 沉积物无法继续沉积在河流末端, 堰强迫性地终止了冲积河流的延长。如果河流末端的沉积物能够得到有效的疏浚, 也能起到与上述模型中堰类似的作用。在Clarke等(2010)的实验中, 通过在冲积扇的末端开挖壕沟疏浚沉积物抑制扇体的扩张, 使得冲积扇表面的河道保持稳定状态, 这暗示河流达到或接近了平衡状态。在Kim等(2013)、Muto等(2016a)、Wang等(2019a)等的实验中, 也通过在河流的末端设置一个水下陡崖(河口区水深梯度无穷大)的方式模拟了强制平衡的河流(图 5)。在这些实验中, 沉积物一旦抵达水下陡崖边缘, 冲积体系无法延长, 所有自上游搬运而来的沉积物全部搬离冲积体系。理论上, 在不考虑蓄水体作用的情况下, 盆地坡度(ϕ )陡于前积层坡度(β ), 即ϕ > β , 便可达到强制平衡的坡度条件。

图 5 三维水槽实验模拟河流的强制平衡(据Wang et al., 2019a)
A— 河流末端为水下“ 悬崖” 从而无法延长, 当前河口相对冲积体系顶点的方位约为20° ~30° ; B— 全实验段的河口方位表明主河道及次级分支河道均表现出稳定性, 河流接近平衡状态Fig.5 A forced graded alluvial river in 3D flume experiment(after Wang et al., 2019a)

4.2 自成因平衡(自动平衡)

4.2.1 自由边界与河流平衡

对于河流末端可以自由延伸的完全自由边界情况, 河流在进积过程中, 若要维持原有的剖面, 一个必要的条件是基准面下降, 且下降的速度与河流剖面的延伸速度(或海岸线的进积速率)成正比。在图 6-A所示的模型中, 海岸线的进积速率(Rpro)与海平面的下降速率(|Rbl|, Rbl> 0为基准面上升, Rbl< 0为基准面下降)存在如下的关系:

|Rbl|=αRpro(1)

其中, α为该河流— 三角洲体系顶积层的坡度。

图 6 稳定沉积物供给、稳定基准面下降背景下, 盆地形态对地层学响应(平衡、侵蚀、加积)的控制作用示意图(据Wang and Muto, 2021)
A— 盆地向海侧基底(下超面)坡度( ϕ)与冲积表面坡度( α)相等( ϕ=α), 河流最终达到平衡。前积层的真实厚度(hset)恰好与临界厚度(hset_crt)相等并且能够维持下去; B— ϕ> α时, hset会持续增大直至hset> hset_crt, 河流最终会侵蚀下切; C— ϕ< α时, hset会持续减小直至hset< hset_crt, 河流加积。直至hset=0, 河流— 三 角洲体系演化为冲积扇。ABT: 河流的冲积段— 基岩段转换点Fig.6 Control of basin configuration to stratigraphic responses(including alluvial grade, degradation and aggradation)with steady sediment supply and base level fall(after Wang and Muto, 2021)

反过来, 冲积体系前积(或进积)也是基准面下降的一个必然结果, 即自上游供给而来的沉积物将优先满足前积的需要。由此可以分为3种情形: (1)如果沉积物的供给量多于前积所需要的, 将有剩余沉积物沉积于河道中, 发生加积; (2)如果上游供给而来的沉积物数量不足以满足前积的需要, 则河流将下切侵蚀以补充新的沉积物; (3)如果前积所需要的沉积物与上游供给量相当, 就实现了平衡。一个有效的度量前积所需沉积物的量是前积层的厚度(hset), 河流实现平衡时的厚度称为临界厚度(hset_crt)。

Muto等(2016a)、Wang和Muto(2021)等人推导并验证了临界厚度的理论解:

二维系统:hset_crt=qs|Rbl|1+α-2(2a)

三维系统:hset_crt≈Qs|Rbl|11+α-2(2b)

其中, qs为单位宽度的沉积物(体积)供给速率(二维); Qs为满宽沉积物(体积)供给速率(三维)。qs=Qs/W(W为河流— 三角洲体系的宽度)。

临界厚度hset_crt反映了单位时间系统前积所需沉积物数量与从上游供给的沉积物数量恰好相等, 无需通过河流侵蚀以产生新的沉积物补充前积, 也没有剩余沉积物使顶积层加积。根据公式(2), 对于恒定的qs(或Qs)和|Rbl|, hset_crt也是确定的。在这种情况下, 如果河流下游三角洲前积层的真实厚度(hset)恰好与hset_crt相等、并且能够维持下去, 则河流就实现了平衡。

另一方面, 三角洲前积层的真实厚度(hset)能否维持一个稳定值取决于蓄水盆地的坡度(或下超面的坡度, ϕ)。如果蓄水盆地的坡度大于冲积表面坡度( ϕ> α), 随着前积的持续进行, hset将不可避免地持续增大(图 6-B); 如果 ϕ< α, 随着前积的持续进行, hset将不可避免地持续减小(图 6-C); 只有 ϕ=α, hset才能维持一个恒定值并保持下去(图 6-A)。

4.2.2 河流的自动平衡(盆地坡度等于冲积表面坡度)

在 ϕ=α的条件下, 同时保证物源供给速率、基准面下降速率恒定, 经过充足的时间, hset=hset_crt的平衡状态总会实现: 如果hset< hset_crt, 则河流— 三角洲体系会通过加积使hset向hset_crt逼近; 如果hset> hset_crt, 则河流— 三角洲体系会通过侵蚀使hset向hset_crt逼近(Wang and Muto, 2021)。在这种(速率)稳定的外部条件下, 河流通过自我调节作用实现平衡状态, 称作自动平衡(autogenic grade; Muto and Swenson, 2006a, 2006b)。如果外界条件如物源供给速率或基准面下降速率发生了改变, 但 ϕ=α的条件仍然能够维持, 则河流会向新的平衡剖面逼近(hset向新的hset_crt逼近)。

Muto和Swenson(2006b)从几何模型的角度论证了这一过程, 并发现: (1)基准面下降速率和沉积物供给速率决定了hset_crt的大小; (2)基准面下降速率和沉积物供给速率的大小不影响河流实现平衡的可行性, 只要其保持不变, 同时 ϕ=α的条件能够维持, 则河流的平衡状态总会实现并维持下去。Muto和Swenson(2006a)进一步通过水槽实验证实了该过程。在图 7所示的剖面中, 在一个前期实现了强制平衡的河流剖面之上(河流坡度保持恒定), 叠置着4套地层。这4套地层的顶界面均与底界面平行, 表明了 ϕ=α的地形条件。每套地层的形成均经历了一个急剧的海平面上升和随后的匀速下降, 在上升过程中, 没有沉积物的供给, 只是将之前形成的河流剖面淹没; 在随后的下降过程中, 保证基准面的匀速下降一和上游沉积物稳定供给。4次基准面下降的速度均不相同(依次加快), 而沉积物供给速率保持一致。这4套地层在前积过程中, 河流均达到了自动平衡状态, 由于基准面下降的速率不同, 平衡时的前积层厚度(hset_crt)各不相同。

图 7 二维水槽实验产生的一系列自成因平衡的河流剖面(据Muto, 2011)(4次实验形成的河流剖面相互平行, 表明4次实验中河流均达到了平衡状态。实验1-实验4基准面下降速度依次增加, 但在每组实验中基准面下降速率恒定。每次实验结束后, 迅速提升基准面, 然后进行下一次实验。每次基准面下降前积层均下超在上次实验形成的、被淹没的平衡剖面上, 从而 ϕ=α。其中, 实验1下超在实验开始之前经强制平衡实现的平衡剖面上。各组实验物源供给条件相同。实验1-实验4前积层厚度减小, 表明随基准面下降速度加快, 代表河流平衡的临界厚度依次减小。具体实验设计见Muto和Swenson, 2006a)Fig.7 Autogenic grade river profiles produced in a series of 2D flume experiments(after Muto, 2011)(Parallel river profiles in 4 experiments reflect the state of grade was attained. Rates of base level fall were constant during each run but increased from Run 1 to Run 4(see the inset diagram). Each run began after a rapid increase of base level rise at the end of the previous run. The foreset prograded on top of the inundated graded river profile so ϕ=α. The foreset of Run 1 prograded on top of a pre-prepared forced graded profile. Upstream water discharge and sediment discharge were kept constant throughout the entire series. The foreset thickness decreased by runs reflects the critical set thickness decreases with increase rate of base level fall. For details on the experimental conditions, see Muto and Swenson, 2006a)

4.3 他成因平衡

很多情况下, ϕ=α的地形条件不容易保证。对于这些情况, 稳定的基准面下降无法实现河流的平衡; 只有通过改变基准面下降的速率(非稳定的外部驱动), 河流平衡才有可能实现。在这样的情况下, 由于河流的平衡状态是在非稳定的外部驱动条件下实现的, 称为他成因的河流平衡(allogenic grade)(Muto et al., 2016a)。

4.3.1 盆地坡度大于冲积表面坡度

如果蓄水盆地的坡度大于冲积表面坡度(ϕ > α ), 随着前积的持续进行, hset将不可避免地持续增大。如果基准面下降速率和沉积物供给速率维持不变(即hset_crt为固定值), hset> hset_crt会不可避免地发生, 沉积体系演化为侵蚀体系(图 6-B)。 ϕ> α背景下, 沉积体系响应于稳定下降基准面必然发生侵蚀的特征已经在水槽实验中得到了证实(Muto and Swenson, 2005; Swenson and Muto, 2007)。可以推测, 在 ϕ> α的情况下, 要想维持河流的平衡, 只有通过: (1)降低基准面下降速率(图 8-A), 或/和(2)增加沉积物供给速率(图 8-B), 以不断增大hset_crt, 使之与河流— 三角洲系统的持续增加的厚度始终相当(hset=hset_crt能够维持)。

图 8 2种他成因的河流平衡机理图解
A— 沉积物稳定供给(供给速率qs保持不变), 如要系统维持河流平衡, 基准面下降速率持续变缓是必要条件; B— 基准面稳定下降(速率Rbl保持不变), 若要维持河流平衡, 相等时段内沉积物充填形成的四边形F1F2B2B1、…、F8F9B9B8面积将逐渐增大, 沉积物供给速率qs持续增加是必要条件, 即qs8> …> qs1。这2种河流平衡的形成伴随着基准面下降速率或沉积物供给速率的变化, 因此是他成因平衡。ABT:河流的冲积段— 基岩段转换点Fig.8 Illustration of two basic allogenic graded rivers

Muto和Swenson(2005)从理论推导了当基准面下降速率随时间(t)的变化满足

Rbl(t)=-ct(3a)

时, 在ϕ > α 的背景下能够始终维持hset=hset_crt, 河流表现为平衡状态(图 8-A)。其中, c是与沉积物供给速率qs、三角洲前缘坡度β 、盆地基底坡度ϕ 、以及沉积物扩散系数 υ有关的系数(Muto and Swenson, 2005):

c=12qs(β-ϕ)1-ϕυqs-11-βυqs-1(3b)

假设沉积物线性扩散, 扩散系数可近似表示为:

υ=qsα(3c)

根据公式3a-3c, 当满足以下条件: (1)稳定的物源供给( qs恒定); (2)盆地的基底坡度稳定不变( ϕ恒定); (3)三角洲的几何学特征稳定不变, 即顶积层坡度( α)与前积层坡度( β)恒定, 实现河流平衡的必要条件是基准面下降速率减缓, 且与时间的平方根成反比。Muto和Swenson(2005)通过设计二维水槽实验, 在满足上述条件的基础上, 使基准面下降随时间的变化符合公式3, 成功模拟了河流的平衡(图 9)。

图 9 二维水槽实验中通过基准面减速下降产生的平衡河流。实验中, 盆地向海侧坡度大于顶积层坡度。基准面的下降速度按公式3a-3c设计。整个实验过程中, ABT(河流的冲积段— 基岩段转换点)几乎静止不动, 表明河流均达到了平衡状态。具体实验设计见Muto和Swenson(2005)Fig.9 A graded river produced by slowing down of base level fall in a 2D flume experiments. In the experiment, the slope of the basin floor is steeper than that of the alluvial river. The rate of base level fall was set by equations 3a-3c. During the experiment, the alluvial-bedrock transition(ABT)was almost stationary reflect the state of grade was attained. For details on the experimental conditions, see Muto and Swenson(2005)

基准面下降与沉积物供给可以互为补充。增加沉积物供给速率与降低基准面下降速率可以起到相似的效果。根据公式3, 在保持基准面下降速率不变的前提下, 使沉积物供给速率正比于时间, 同样可以维持河流的平衡。

4.3.2 盆地坡度小于冲积表面坡度

如果蓄水盆地的坡度小于河床的坡度(ϕ < α ), 则hset随着前积的进行持续减小。如果基准面下降速率和沉积物供给速率维持不变(即hset_crt为固定值), hset< hset_crt会不可避免地发生, 沉积体系演化为加积体系。Petter和Muto(2008)通过水槽实验证实了在 ϕ< α背景下, 沉积体系响应于稳定下降基准面和稳定供给沉积物必然发生加积的特性。

同样可以推测, 对于先前存在的河流— 三角洲体系(hset> 0), 在 ϕ< α的情况下, 只有通过: (1)加快基准面下降速率, 或/和(2)减小沉积物供给速率, 以不断减小hset_crt, 使之与河流— 三角洲系统的厚度始终保持hset=hset_crt, 才有可能维持河流的平衡。但是, 随着前积的持续进行, hset将不可避免地减小至0。此时, 基准面与沉积体系脱离, 前积层消失, 河流— 三角洲体系演化为冲积扇体系, 沉积体系将持续加积。因此, 在 ϕ< α的背景下, 河流的平衡只能存在于特定的时间段, 并不能无休止地持续进行下去。

5 讨论

由于河流达到平衡状态后河床不再发生净侵蚀作用和净沉积作用, 这意味着平衡的河流很难在地质记录中留下痕迹而识别出来。因此现有对河流平衡的研究多集中在过程模拟和现代沉积考察。本节的讨论也因此限制在河流实现平衡状态的控制机理和对现代沉积的探索。但作者并不排除在地层记录中能够识别平衡的河流体系的可能性。如果一个河流— 三角洲体系在某一时期仅在下游端发育前积层(顶超)、且上游端ABT有证据表明固定不变, 又或者, 陆相河流部分既不发育顶积层, 也无明显的侵蚀下切作用, 或河流只发生侧向迁移而无垂向的侵蚀或抬升, 则意味着该河流— 三角洲体系在该时期可能达到了平衡状态, 如下文5.2.2所讨论的湄公河三角洲自~3000年以来仅发育前积层就是一个例子。

5.1 基准面变化、盆地形态与河流平衡的实现

文中讨论的河流平衡是指河流在整个冲积区的平衡, 应当充分考虑冲积河流的边界具有自由移动的特征。冲积河流体系具有3个自由移动边界: 海岸线、ABT(相当于上超点)、前积层下超点。其中, 基准面的升降直接决定了海岸线的移动。海岸线的移动又是与ABT、下超点联动的, 这种联动作用控制着沉积物在水上和水下的分配。

在这种背景下, 3个方面的地质条件对河流的平衡起到关键的控制作用: (1)物源供给, 包括沉积物供给速率(沉积物体积流量, qs)与上游来水流量(qw), 其中, qs决定了河流达到平衡需要在水下分配沉积物的总量, qw(或qs/qw)决定了冲积体系的扩散系数( υ, 或表面坡度 α)(Swenson et al., 2000); (2)盆地的几何形态, 主要是下超面的坡度( ϕ), 决定沉积物在水下或前积层中的分配, 也决定了下超点移动的速率; (3)冲积体系的几何形态, 包括顶积层坡度( α)以及前积层坡度( β), 间接决定了沉积物的分配。

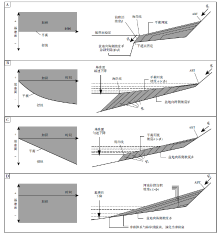在上述地质条件一定且保持稳定的假设下, 基准面只有通过特定的方式演化才能实现河流的平衡: 只有当基准面距离盆地底部的距离恰好容纳沉积物供给总量, 河流的平衡才能实现; 当基准面距离盆地底部的距离小于容纳全部沉积物所需, 则冲积体系发生加积, 反之则冲积体系遭受侵蚀。从这种意义上来看, 对基准面的讨论除了要重视其绝对位置之外, 讨论其距离盆地底部的相对位置也十分必要。对于盆地水深梯度极大的情况( ϕ> β), 河流的平衡无需基准面变化(强制平衡)(图 10-A); 对于盆地基底坡度不小于冲积平原坡度的情况( α≤ϕ< β), 河流的平衡需要基准面特定形式的下降(他成因平衡, 图 10-B; 或自成因平衡, 图 10-C); 对于盆地基底坡度小于冲积平原坡度的情况( ϕ< α), 在其他外部条件恒定不变的情况下, 河流在基准面加速下降的背景下可能在短时期内达到平衡, 但长期来看平衡状态无法维持, 最终演化为净加积的体系(图 10-D)。

图 10 不同盆地形态背景下基准面变化(基准面相对于横轴向上为上升、向下为下降)与河流— 三角洲体系平衡、侵蚀与加积的关系(据Muto et al., 2007, 2016a; 有修改)
A— 在盆地水深梯度很大、向海侧坡度( ϕ)很陡且大于前积层坡度(β )的背景下( ϕ> β), 河流平衡于稳定的基准面: 基准面上升, 河流加积; 基准面下降, 河流侵蚀下切。B— 盆地向海侧坡度( ϕ)较陡、大于顶积层坡度(α )的背景下( ϕ> α), 基准面减速下降是河流达到平衡的必要条件。C— ϕ=α的背景下, 基准面稳定(匀速)下降是河流达到平衡的必要条件。D— ϕ< α的背景下, 无论基准面上升或下降, 冲积体系具有持续加积的特性。假设沉积物供给速率(qs)稳定不变。ABT: 河流的冲积段— 基岩段转换点Fig.10 Relationship between base level change(base level is falling below and rising above the horizontal axis)and the state of alluvial-delta(graded, degradation, aggradation)for different basin geometries(modified from Muto et al., 2007, 2016a)

如果从冲积河流整体的尺度来看, 传统观点认为在一切外部条件保持稳定的背景下: (1)河流平衡于稳定的基准面, 以及(2)平衡是河流力图达到的最终状态, 只有在特定的地质背景下才能成立。对于强制平衡, 以上2种观点均成立; 对于自成因平衡, 河流只有在稳定下降的基准面背景下、经过足够的调整时间才可发生, 因此只有观点(2)成立; 对于他成因平衡, 由于基准面的减速下降(或非稳定下降)是必要条件, 因此以上2种观点均不成立。

5.2 自然界中河流平衡的可能性

河流可以通过多种方式达到平衡状态, 地质历史时期达到或接近达到平衡状态的河流应多于传统观点认为的那样, 河流平衡的概念不再局限于理论意义, 而是非常有可能在自然界发生。

5.2.1 自然界中的强制平衡河流

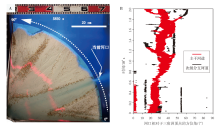
河流强制平衡在自然界是可能实现的。在自然界中, 如果河流的末端由于某些地质原因使得冲积体系的延长受到抑制, 河流将向强制平衡的趋势演化。实现强制平衡的一种情形是河流汇入水深梯度较大的蓄水盆地。例如, 中国台湾东部所面临的太平洋缺少明显的大陆架, 河流汇入后很快面临深水环境(图 11)。在台湾东北岸线注入太平洋的立雾溪河口向海洋方向仅3 km水深急剧增加至400~500 m(图 11-B)。另一方面, 立雾溪末端的三角洲平原分流河道在过去200~2000年保持稳定。Wang等(2019a)的研究表明, 由于水深较大的缘故, 立雾溪搬运而来的沉积物仅有1%~2%保留在了三角洲平原, 其余的绝大多数沉积物均沉积于水下, 表明立雾溪接近了平衡状态。随着三角洲进积的水深进一步增加(图 11-B), 如果物源、海平面等外部条件保持不变, 立雾溪三角洲分流河道的稳定性可能会持续下去(Wang et al., 2019a)。

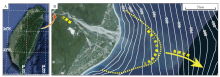图 11 立雾溪三角洲的地理位置(A)及地貌特征(B)(据Google Earth)。立雾溪三角洲前缘的太平洋水深梯度很大, 其平原上的分流河道在过去200~2000年来保持稳定状态(据Wang et al., 2019a)Fig.11 Location(A)and geomorphologic characteristics(B)of Liwu River delta(from Google Earth). The water depth gradient of the Pacific Ocean in front of Liwu River delta is very large. The channel on top of the delta plain has been kept stable during the past 200~2000 years(after Wang et al., 2019a)

有利于实现强制平衡的另外一种情形是蓄水体存在的波浪、沿岸流、或潮汐等作用能有效疏浚河流搬运来的沉积物。例如, Swenson通过数值模拟证明了当河口区波浪扩散沉积物的能力与河流的输入能力之比提高1个数量级, 河道的沉积速率和决口周期将以50为系数分别降低和提高(Swenson, 2005); 再如, 对于很多受潮汐影响或控制的三角洲, 分流河道表现的比较稳定(Geleynse et al., 2011; Gugliotta and Saito, 2019), 这些都表明河口区沉积物的疏散有利于河流向平衡状态接近。

5.2.2 自然界中的自成因平衡河流

河流自动平衡的条件在自然界也容易实现。在地质历史中, 基准面呈周期性升降变化, 在每个下降半周期, 三角洲将前积并下超在前半个上升半周期形成的大陆架上。Wang和Muto(2021)通过实验证明, 对于充分扩张的冲积体系(冲积河流的长度足够长), 在其面临海平面上升时, 海侵所形成的大陆架与上升之前的冲积体系坡度相当, 即大陆架是海平面上升前的冲积体系被淹没而形成。这样一来, 在下一次基准面下降时, 大陆架的坡度与前积在其上的冲积河流体系坡度相当的必要条件便得以实现。如果海平面下降速度也能够保持稳定, 则在自然界自动平衡的河流就有存在的可能。

Wang等(2019b)基于这样的认识, 认为湄公河下游段自3.5 ka至今基本达到了自动平衡状态(图 12)。在末次盛冰期, 海平面降至陆架边缘附近, 古湄公河延伸至越南陆架边缘。冰后期全新世的海平面快速上升, 海岸线后退, 曾经的冲积平原被淹没, 形成大陆架。随着8.4~6.3 ka海平面上升速度减缓、至6.3~3.5 ka海平面达到高位, 湄公河三角洲形成(Ta et al., 2005; Anthony et al., 2015), 并下超在之前海侵形成的大陆架上。据测量, 现今大陆架的坡度约为1× 10-4; 现今三角洲平原的坡度约为0.3× 10-4, ϕ=α的条件基本实现(Wang et al., 2019b)(图 12-C)。

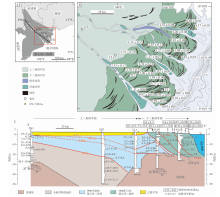图 12 湄公河三角洲的地貌学与地层学特征(据Tamura et al., 2009, 2012; Wang et al., 2019b)
A— 湄公河三角洲地理位置及钻孔位置。红框指示B所示的范围。黑色实线指示C所示的剖面; B— 湄公河三角洲平原及临近海域地貌学特征(范围见图A)。三角洲平原上发育完好的滩脊系统。滩脊的年龄显示海岸线自约3500年以来持续后退。滩脊系统的完整保存表明3500年以来河道是稳定的, 三角洲平原没有明显的侵蚀作用、也没有加积作用发生; C— 湄公河三角洲8000年以来的等时地层格架(剖面位置见图A)。自3500年前以来, 三角洲只发育前积层, 缺少顶积层, 表明分流河道所搬运的沉积物全部分配于水下, 河流达到平衡状态Fig.12 Geomorphologic and stratigraphic characteristics of the Mekong River delta(after Tamura et al., 2009, 2012; Wang et al., 2019b)

在随后的3.5 ka至今, 在新构造作用的影响下, 相对海平面以|Rbl|=9.0× 10-4 m/yr的速率缓慢下降(Ta et al., 2002)。假设全新世湄公河的沉积物年均输送量保持不变, Qs=(1.0~1.2)× 108 m3/yr(Milliman and Meade, 1983; Ta et al., 2002; Liu et al., 2017), 根据公式2b计算出来的河流达到平衡时河流— 三角洲体系的理论厚度为26~33 m。这一数据与湄公河三角洲的真实厚度20~25 m相当(是真实厚度的1.04~1.65倍), 表明湄公河三角洲分流河道几乎接近了平衡状态(Wang et al., 2019b)。

湄公河三角洲平原上普遍发育滩脊, 这些滩脊记录了古海岸线的位置。这些滩脊分布于近乎顺直的分流河道之间, 既没有被分流河道侵蚀、也没有被埋藏, 表明(1)分流河道自滩脊发育以来是稳定的, 没有决口和改道, 且保持线性延伸; (2)分流河道有效输送沉积物至海洋, 没有明显的侵蚀和沉积作用发生。这些都为河流的平衡提供了证据。滩脊的年龄表明, 这种近似平衡的状态从3.5 ka持续至今(Tamura et al., 2012; Wang et al., 2019b)(图 12-B)。

这是第1次在自然界发现河流通过自成因机制达到或接近平衡的现象(Wang et al., 2019b)。当然, 潮汐、波浪、洋流、三角洲平原上发育的植被也可能为河流的近似平衡做出了一定的贡献。但是, 随着人类世湄公河上游流域的采砂、筑坝等行为, 以及近年全球海平面的上升, 这种平衡状态将被逐渐打破。

5.2.3 自然界中的他成因平衡河流

相较而言, 河流通过他成因机制达到平衡显得更加困难。例如, 对于 ϕ> α的情况, 在物源供给保持稳定的前提下, 基准面需要按照图 8-A或图10-B所示的曲线下降; 如果基准面的下降不满足图 8-A或图10-B所示的曲线, 则需要物源供给的同步调整以维持公式3的成立。这种多种条件的精妙的“ 配合” 显得更难以实现。但是, 如果公式3能够在多种作用下得以满足并维持, 河流通过他成因机制达到平衡状态也不无可能。对于 ϕ< α的情况同样如此。

5.3 基准面下降过程中的河流加积现象: 对成因地层学的启示

层序地层学的出现使地质人员除了重视地层的等时性之外, 也开始重视地层的成因(Catuneanu et al., 2009)。例如, 层序定义为“ 由不整合面或与不整合面相对应的整合面作为边界的、一个相对整合的、有内在联系的地层序列” (Vail et al., 1977; Posamentier et al., 1988; 纪友亮和周勇, 2020; 朱筱敏, 2023)。有内在联系的地层序列是经由进积、退积、加积、侵蚀4种基本过程而形成(Catuneanu, 2019; Catuneanu and Zecchin, 2020): 它们响应于特定的外部驱动条件(主要是物源供给、海平面升降、构造沉降等), 或同时、或交替发生形成地层。层序地层学的一个重要应用是根据地层记录中地层叠置的样式恢复外部驱动条件和地层叠置的过程, 因此探究4种地层叠置的基本过程与外部驱动条件的对应关系是核心问题。近年来, 成因地层学(genetic stratigraphy)的概念屡次被提及(Muto et al., 2007; Karamitopoulos et al., 2021), 强调从过程上认识地层叠置的机制, 以对地层叠置过程与外部驱动条件的对应关系有更为清晰的认识。

文中的分析表明河流加积与侵蚀的临界点发生在基准面下降过程中, 而非传统观点认为的基准面稳定不变。越来越多的证据也表明, 即使基准面下降, 河流— 三角洲体系不总表现为侵蚀, 也可能表现为加积(Schumm, 1993; Blum and Tö rnqvist, 2000; Van Heijst and Postma, 2001; Browne and Naish, 2003; Muto and Steel, 2004; Petter and Muto, 2008; Strong and Paola, 2008; Nijhuis et al., 2015; Catuneanu and Zecchin, 2016), 甚至达到平衡状态(Nummedal et al., 1993; Schumm, 1993; Leeder and Stewart, 1996; Muto and Swenson, 2005, 2006a, 2006b; Wang et al., 2019b; Wang and Muto, 2021)。这可以通过基准面下降过程中前积层的真实厚度(hset)与理论平衡厚度(hset_crt)的对比进行合理地解释: 基准面下降过程中的加积是由于hset< hset_crt; 发生侵蚀是因为hset> hset_crt。

在经典的层序地层学模式中, 响应于基准面下降的地层叠置过程往往被认为是单一的。例如, 以Posamentier、Catuneanu等为代表的学者将此过程统一称为强制海退(Posamentier et al., 1992; Catuneanu et al., 2009); 由此构成的地层叠置样式也较为单一, 以阶梯式下降前积或退覆为主(progradational and downstepping或offlap)。而实际上, 强制海退过程中的地层叠置应该更为复杂一些: 前积是否表现为“ 阶梯式下降” 式的“ 退覆” 取决于前积过程中河流— 三角洲体系的厚度(hset)与代表平衡的理论厚度(hset_crt)的相对大小。在强制海退的早期和晚期(假设基准面呈正弦曲线式变化), 基准面下降速率较小, 理论平衡厚度(hset_crt)大(公式2)(图 13), hset< hset_crt的条件容易实现, 河流倾向于加积而发育顶积层(非“ 阶梯式下降前积” ); 而在强制海退的中间阶段, 基准面下降速率最大, 河流— 三角洲体系的理论平衡厚度(hset_crt)小(公式2)(图 13), hset> hset_crt的条件容易实现, 从而河流倾向于侵蚀下切、不发育顶积层、表现为“ 阶梯式下降” 式的“ 退覆” 。

图 13 基准面下降半旋回(阴影部分)过程中变化速率及指示河流平衡状态的河流— 三角洲体系临界厚度对应关系(基准面在下降的早期和晚期(a, c), 速率慢, 对应的临界厚度最大, 一般会大于实际厚度, 河流— 三角洲体系进积的同时加积。在下降中期(b), 速率最快, 对应的临界厚度最小, 河流倾向于下切侵蚀。但是, 如果在基准面下降晚期海岸线推至陆架坡折附近甚至之下, 由于水深梯度的陡增, 很容易使得河流— 三角洲体系的实际厚度大于临界厚度, 从而诱发侵蚀, 如图c-2所示)Fig.13 The rate and critical delta-set thickness which indicates alluvial grade during the falling half cycle of base level change(the shaded part)(At the initial and late phase of base level fall(a, c), the rate of the fall is slow. Correspondingly, the critical set thickness would be large, which is very likely to be larger than the actual set thickness. As a consequence, the alluvial-delta system progrades with aggradation. At the middle phase of base level fall(b), the rate of the fall is rapid. Correspondingly, the critical set thickness would be small, which is very likely to be smaller than the actual set thickness. As a consequence, the alluvial-delta system degrades. It should be noted that at the late stage of the fall, the shoreline might regress to even below the shelf edge. Owing to the significant increase of bathymetry, the actual set thickness of the prograding delta would easily exceed the theoretical value, which would trigger fluvial incision. See Fig.c-2 for illustration)

当然, 在强制海退的晚期, 岸线可能已经推进到陆架坡折处甚至以下。在这里, 水深梯度陡增, 河流— 三角洲体系的真实厚度也会显著增加, 使得hset> hset_crt容易实现, 从而诱发下切谷的形成。这可以解释早期层序地层学I型层序边界的形成(Posamentier and Vail, 1988; Van Wagoner et al., 1988, 1990; Wescott, 1993), 也可以解释陆架边缘型三角洲比陆架型三角洲在相对海平面下降过程中分流河道更容易下切侵蚀的现象(Porebski and Steel, 2006)。

6 结论

源汇系统中冲积体系的3个边界, 即河流的冲积段— 基岩段转换点(ABT)、岸线、前积层下超点, 具有自由移动的特性。讨论冲积河流全河段的平衡应该充分考虑自由边界特征。在这样的背景中, 河流的平衡受基准面的控制; 基准面的作用方式进一步取决于盆地的形态。据此可以推导河流达到平衡的三种方式: 强制平衡(只有ABT一个自由移动边界)、自成因平衡(3个自由移动边界)、他成因平衡(3个自由移动边界)。这对传统认识中河流达到平衡的条件做出了补充。

如果某些地质作用使得河流的末端无法自由延长, 如河流的末端为水下陡坡, 或者蓄水体的波浪、潮汐等作用能够有效疏浚河口区沉积物, 则河流可以在基准面稳定不变的情况下达到平衡状态, 这种通过强制性地抑制河流的延长而达到的河流平衡, 称作强制平衡。传统观点认为的: (1)河流平衡于稳定的基准面; (2)平衡是河流的最终状态(在外界条件保持稳定前提下), 对于强制平衡均适用。

如果河流的末端能够自由延长, 则基准面下降是河流达到平衡的必要条件。基准面下降的方式进一步取决于盆地的形态。(1)盆地坡度(下超面坡度)与顶积层坡度相当, 河流可以在基准面匀速(稳定)下降的情况下达到平衡, 称作自动平衡(或自成因平衡)。传统观点认为的平衡是河流的最终状态适用于自成因平衡。(2)盆地坡度(下超面坡度)大于顶积层坡度, 基准面须以特定的速率减速下降河流才能达到平衡, 称作他成因平衡。对于他成因平衡, 传统观点关于河流平衡的两条认识均不适用。

多数情况下, 河流加积与侵蚀的临界状态取决于基准面下降, 而非传统观点认为的基准面稳定不变。基准面下降过程中河流— 三角洲体系前积层的厚度可作为河流平衡与否的一个指标。传统成因地层学中关于地层的叠置过程需要进一步认识。

致谢 感谢日本长崎大学Tetsuji Muto教授对撰写此文的支持, 并提供图 4、图 7、图 9所示的实验资料。感谢朱筱敏教授的组稿和邀请。2位匿名专家在审稿过程中提出了宝贵意见, 对论文的改进帮助很大, 一并表示感谢。祝贺中国石油大学成立70周年。

(责任编辑 李新坡; 英文审校 李 攀)

参考文献
[1] 操应长, 徐琦松, 王健. 2018. 沉积盆地“源-汇”系统研究进展. 地学前缘, 25(4): 116-131.
[Cao Y C, Xu Q S, Wang J. 2018. Progress in “Source-to-Sink”system research. Earth Science Frontiers, 25(4): 116-131] [文内引用:1]
[2] 陈星渝, 张志杰, 万力, 袁选俊, 周川闽, 成大伟, 刘银河. 2023. 深时源-汇系统要素的常用定量分析方法. 地质科技通报, 1-17. DOI: 1019509/j.cnki.dzkq.tb20220277.
[Chen X Y, Zhang Z J, Wan L, Yuan X J, Zhou C M, Cheng D W, Liu Y H. 2023. Quantitative analysis methods of source-to-sink systems in deep time and its progress. Bulletin of Geological Science and Technology, 1-17] [文内引用:1]
[3] 邓彩云, 黄河清, 刘晓芳, 范北林. 2015. 冲积河流平衡理论在长江中下游河床演变中的应用性检验. 泥沙研究, (1): 55-60, 74.
[Deng C Y, Huang H Q, Liu X F, Fan B L. 2015. Evaluation of the applicability of equilibrium theory for alluvial channel flow in the middle and Lower Yangtze River. Journal of Sediment Research, (1): 55-60, 74] [文内引用:1]
[4] 邓宏文, 王红亮, 宁宁. 2000. 沉积物体积分配原理: 高分辨率层序地层学的理论基础. 地学前缘, 7(4): 305-313.
[Deng H W, Wang H L, Ning N. 2000. Sediment volume partition principle: Theory basis for high-resolution sequence stratigraphy. Earth Science Frontiers, 7(4): 305-313] [文内引用:1]
[5] 龚承林, Steel R J, 彭旸, 王英民, 李东伟. 2021. 深海碎屑岩层序地层学50年(1970—2020)重要进展. 沉积学报, 40(2): 292-318.
[Gong C L, Steel R J, Peng Y, Wang Y M, Li D W. 2021. Major advances in deep-marine siliciclastic sequence stratigraphy, 1970 to 2020. Acta Sedimentolocica Sinica, 40(2): 292-318] [文内引用:1]
[6] 纪友亮, 周勇. 2020. 层序地层学(第二版). 北京: 中国石化出版社.
[Ji Y L, Zhou Y. 2020. Sequence Stratigraphy(2nd Edition). Beijing: China Petrochemical Press] [文内引用:2]
[7] 林畅松, 夏庆龙, 施和生, 周心怀. 2015. 地貌演化、源-汇过程与盆地分析. 地学前缘, 22(1): 9-20.
[Lin C S, Xia Q L, Shi H S, Zhou X H. 2015. Geomorphological evolution, source to sink system and basin analysis. Earth Science Frontiers, 22(1): 9-20] [文内引用:1]
[8] 马字发, 张会平, 马元旭, 赵旭东. 2022. 河道沉积物粒度沿程变化特征及其影响因素. 地质学报, 96(10): 3658-3673.
[Ma Z F, Zhang H P, Ma Y X, Zhao X D. 2022. Downstream changes of riverbed grain size and its controls. Acta Geologica Sinica, 96(10): 3658-3673] [文内引用:1]
[9] 邵龙义, 王学天, 李雅楠, 刘炳强. 2019. 深时源-汇系统古地理重建方法评述. 古地理学报, 21(1): 67-81.
[Shao L Y, Wang X T, Li Y N, Liu B Q. 2019. Review on palaeogeographic reconstruction of deep-time source-to-sink systems. Journal of Palaeogeography(Chinese Edition), 21(1): 67-81] [文内引用:1]
[10] 王嗣敏, 刘招君. 2001. 基准面与可容空间变化分析及应用. 世界地质, 20(1): 1-7.
[Wang S M, Liu Z J. 2001. The analysis of base-level and accommodation space change and its application. World Geology, 20(1): 1-7] [文内引用:1]
[11] 邬金华, 毛志超, 张哲. 1997. 河相层序地层研究进展述评. 地质科技情报, 16(3): 40-46.
[Wu J H, Mao Z C, Zhang Z. 1997. Review of the development of fluvial sequence stratigraphy. Geological Science and Technology Information, 16(3): 40-46] [文内引用:1]
[12] 徐长贵, 杜晓峰, 徐伟, 赵梦. 2017. 沉积盆地“源-汇”系统研究新进展. 石油与天然气地质, 38(1): 1-11.
[Xu C G, Du X F, Xu W, Zhao M. 2017. New advances of the “Source-to-Sink”system research in sedimentary basin. Oil & Gas Geology, 38(1): 1-11] [文内引用:1]
[13] 朱红涛, 徐长贵, 朱筱敏, 曾洪流, 姜在兴, 刘可禹. 2017. 陆相盆地源-汇系统要素耦合研究进展. 地球科学, 42(11): 1851-1870.
[Zhu H T, Xu C G, Zhu X M, Zeng H L, Jiang Z X, Liu K Y. 2017. Advances of the source-to-sink units and coupling model research in continental basin. Earth Science, 42(11): 1851-1870] [文内引用:1]
[14] 朱筱敏. 2023. 层序地层学. 山东东营: 中国石油大学出版社.
[Zhu X M. 2023. Sequence Stratigraphy. Shand ong Dongying: China University of Petroleum Press] [文内引用:2]
[15] 朱筱敏, 谈明轩, 董艳蕾, 李维, 秦祎, 张自力. 2019. 当今沉积学研究热点讨论: 第20届国际沉积学大会评述. 沉积学报, 37(1): 1-16.
[Zhu X M, Tan M X, Dong Y L, Li W, Qin Y, Zhang Z L. 2019. Current hot topics of sedimentology: comment on the 20th international sedimentological congress. Acta Sedimentologica Sinica, 37(1): 1-16] [文内引用:1]
[16] Allen P A. 2008. From land scapes into geological history. Nature, 451: 274-276. [文内引用:1]
[17] Allen P A, Allen J R. 2005. Basin Analysis: Principles and Applications(version 2nd ed). Chichester, UK: Wiley-Blackwell, 1-549. [文内引用:1]
[18] Anthony E J, Brunier G, Besset M, Goichot M, Dussouillez P, Nguyen V L. 2015. Linking rapid erosion of the Mekong River delta to human activities. Scientific Reports, 5: 14745. [文内引用:1]
[19] Barrell J. 1912. Criteria for the recognition of ancient delta deposits. Geological Society of America Bulletin, 23: 377-446. [文内引用:1]
[20] Bates R L, Jackson J A. 1987. Glossary of Geology, 3rd Ed. Alexand ria, VA. : American Geological Institute, 788. [文内引用:2]
[21] Bijkerk J F, Eggenhuisen J T, Kane I A, Meijer N, Waters C N, Wignall P B, McCaffrey W D. 2016. Fluvio-marine sediment partitioning as a function of basin water depth. Journal of Sedimentary Research, 86: 217-235. [文内引用:2]
[22] Blom A, Viparelli E, Chavarrías V. 2016. The graded alluvial river: profile concavity and downstream fining. Geophysical Research Letters, 43: 6285-6293. [文内引用:3]
[23] Blum M D, Törnqvist T E. 2000. Fluvial responses to climate and sea-level change: a review and look forward. Sedimentology, 47: 2-48. [文内引用:1]
[24] Bolla Pittaluga M, Luchi R, Seminara G. 2014. On the equilibrium profile of river beds. Journal of Geophysical Research: Earth Surface, 119(2): 317-332. [文内引用:3]
[25] Browne G H, Naish T R. 2003. Facies development and sequence architecture of a late Quaternary fluvial-marine transition, Canterbury plains and shelf, New Zealand : implications for forced regressive deposits. Sedimentary Geology, 158(1-2): 57-86. [文内引用:1]
[26] Catuneanu O. 2006. Principles of Sequence Stratigraphy. Amsterdam: Elsevier, 1-375. [文内引用:1]
[27] Catuneanu O. 2019. Model-independent sequence stratigraphy. Earth-Science Reviews, 188: 312-388. [文内引用:3]
[28] Catuneanu O, Abreu V, Bhattacharya J P, Blum M D, Dalrymple R W, Eriksson P G, Fielding C R, Fisher W L, Galloway W E, Gibling M R, Giles K A, Holbrook J M, Jordan R, Kendall C G St C, Macurda B, Martinsen O J, Miall A D, Neal J E, Nummedal D, Pomar L, Posamentier H W, Pratt B R, Sarg J F, Shanley K W, Steel R J, Strasser A, Tucker M E, Winker C. 2009. Towards the stand ardization of sequence stratigraphy. Earth-Science Reviews, 92: 1-33. [文内引用:3]
[29] Catuneanu O, Zecchin M. 2016. Unique vs. non-unique stratal geometries: relevance to sequence stratigraphy. Marine and Petroleum Geology, 78: 184-195. [文内引用:1]
[30] Catuneanu O, Zecchin M. 2020. Parasequences: allostratigraphic misfits in sequence stratigraphy. Earth-Science Reviews, 208: 103289. [文内引用:1]
[31] Chang H H. 1986. River channel changes: adjustments of equilibrium. Journal of Hydraulic Engineering, 112(1): 43-55. [文内引用:2]
[32] Clarke L, Quine T A, Nicholas A. 2010. An experimental investigation of autogenic behaviour during alluvial fan evolution. Geomorphology, 115(3-4): 278-285. [文内引用:1]
[33] Cross T A, Homewood P W. 1997. Amanz Gressly̓s role in founding modern stratigraphy. Geological Society of America Bulletin, 109(12): 1617-1630. [文内引用:1]
[34] Cross T A, Lessenger M A. 1998. Sediment volume partitioning: rationale for stratigraphic model evaluation and high-resolution stratigraphic correlation. In: Gradstein F M, Sand vik K O, Milton N J(eds). Sequence Stratigraphy: Concepts and Applications. Norwegian Petroleum Society(NPF)Special Publication, 8: 171-195. [文内引用:1]
[35] Davis W M. 1902. Baselevel, grade and peneplain. The Journal of Geology, 10(1): 77-111. [文内引用:4]
[36] Ferrer-Boix C, Chartrand S M, Hassan M A, Martín-Vide J P, Parker G. 2016. On how spatial variations of channel width influence river profile curvature. Geophysical Research Letters, 43: 6313-6323. [文内引用:1]
[37] Geleynse N, Storms J E A, Walstra D J R, Albert Jagers H R, Wang Z B, Stive M J F. 2011. Controls on river delta formation: insights from numerical modelling. Earth and Planetary Science Letters, 302(1-2): 217-226. [文内引用:1]
[38] Gilbert G K. 1877. Geology of the Henry Mountains. Washington, D. C. : U. S. Government Printing Office, 160. [文内引用:1]
[39] Green J F N. 1936. The terraces of southernmost England . Quarterly Journal of the Geological Society of London, 92(part 2): 58-88. [文内引用:1]
[40] Gugliotta M, Saito Y. 2019. Matching trends in channel width, sinuosity, and depth along the fluvial to marine transition zone of tide-dominated river deltas: the need for a revision of depositional and hydraulic models. Earth-Science Reviews, 191: 93-113. [文内引用:1]
[41] Holbrook J, Scott R W, Oboh-Ikuenobe F E. 2006. Base-level buffers and buttresses: a model for upstream versus downstream control on fluvial geometry and architecture within sequences. Journal of Sedimentary Research, 76(1): 162-174. [文内引用:1]
[42] Jervey M T. 1988. Quantitative geological modeling of siliciclastic rock sequences and their seismic expression. In: Wilgus C K, Hastings B S, Kendall C G St C, Posamentier H W, Ross C A, van Wagoner J C(eds). Sea Level Changes: An Integrated Approach. SEPM(Society of Economic Paleontologists and Mineralogists)Special Publication, 42: 47-69. [文内引用:3]
[43] Johnson D D, Beaumont C. 1995. Preliminary results from a planform kinematic model of orogen evolution, surface processes and the development of clastic foreland basin stratigraphy. In: Dorobek S L, Ross G M(eds). Stratigraphic Evolution of Foreland Basins. SEPM(Society of Economic Paleontologists and Mineralogists)Special Publication, 52: 3-24. [文内引用:1]
[44] Karamitopoulos P, Weltje G J, Dalman R A F. 2021. Large-scale connectivity of fluvio-deltaic stratigraphy: inferences from simulated accommodation-to-supply cycles and automated extraction of chronosomes. Basin Research, 33(1): 382-402. [文内引用:2]
[45] Kesseli J E. 1941. The concept of the graded river. The Journal of Geology, 49(6): 561-588. [文内引用:4]
[46] Kim Y, Kim W, Cheong D, Muto T, Pyles D R. 2013. Piping coarse-grained sediment to a deep water fan through a shelf-edge delta bypass channel: tank experiments. Journal of Geophysical Research: Earth Surface, 118(4): 2279-2291. [文内引用:1]
[47] Leeder M R, Stewart M D. 1996. Fluvial incision and sequence stratigraphy: alluvial responses to relative sea-level fall and their detection in the geological record. In: Hesselbo S P, Parkinson D N(eds). Sequence Stratigraphy in British Geology, Geological Society, London, Special Publications, 103: 25-39. [文内引用:2]
[48] Leopold L B, Bull W B. 1979. Base level, aggradation, and grade. Proceedings of the American Philosophical Society, 123: 168-202. [文内引用:1]
[49] Li W, Wang Z B, de Vriend H J, van Maren D S. 2014. Long-term effects of water diversions on the longitudinal flow and bed profiles. Journal of Hydraulic Engineering, 140(6): 04014021. [文内引用:1]
[50] Liu J P, DeMaster D J, Nguyen T T, Saito Y, Nguyen V L, Ta T K O, Li X. 2017. Stratigraphic formation of the Mekong River delta and its recent shoreline changes. Oceanography, 30: 72-83. [文内引用:1]
[51] Mackin J H. 1948. Concept of the graded river. Geological Society of America Bulletin, 59: 463-512. [文内引用:4]
[52] Miall A D. 2010. The Geology of Stratigraphic Sequences, 2nd Ed. Berlin Heidelberg: Springer-Verlag, 316. [文内引用:1]
[53] Milliman J D, Meade R H. 1983. World-wide delivery of river sediment to the oceans. The Journal of Geology, 91: 1-21. [文内引用:1]
[54] Muto T. 2011. A new view of fluvial grade revealed by model experiments: alluvial response in the lower reaches of rivers to sea level. The Journal of the Geological Society of Japan, 117: 172-182. [文内引用:1]
[55] Muto T, Steel R J. 2000. The accommodation concept in sequence stratigraphy: some dimensional problems and possible redefinition. Sedimentary Geology, 130: 1-10. [文内引用:1]
[56] Muto T, Steel R J. 2004. Autogenic response of fluvial deltas to steady sea-level fall: implications from flume-tank experiments. Geology, 32(5): 401-404. [文内引用:1]
[57] Muto T, Swenson J B. 2005. Large-scale fluvial grade as a non-equilibrium state in linked depositional systems: theory and experiment. Journal of Geophysical Research: Earth Surface, 110(F), F03002. [文内引用:7]
[58] Muto T, Swenson J B. 2006a. Autogenic attainment of large-scale alluvial grade with steady sea-level fall: an analog tank-flume experiment. Geology, 34: 161-164. [文内引用:4]
[59] Muto T, Swenson J B. 2006b. Controls on alluvial aggradation and degradation during steady fall of relative sea level: flume experiments. In: Parker G, Garcia M H(eds). Proceedings of the 4th IAHR Symposium of River, Coastal and Estuarine Morphodynamics. London: Taylor & Francis Group, 665-674. [文内引用:5]
[60] Muto T, Steel R J, Swenson J B. 2007. Autostratigraphy: a framework norm for genetic stratigraphy. Journal of Sedimentary Research, 77(1): 2-12. [文内引用:2]
[61] Muto T, Furubayashi R, Tomer A, Sato T, Kim W, Naruse H, Parker G. 2016a. Planform evolution of deltas with graded alluvial topsets: insights from three-dimensional tank experiments, geometric considerations and field applications. Sedimentology, 63(7): 2158-2189. [文内引用:4]
[62] Muto T, Steel R J, Burgess P M. 2016b. Contributions to sequence stratigraphy from analogue and numerical experiments. Journal of the Geological Society, 173(5): 837-844. [文内引用:1]
[63] Nijhuis A G, Edmonds D A, Caldwell R L, Cederberg J A, Slingerland R L, Best J L, Parsons D R, Robinson R A J. 2015. Fluvio-deltaic avulsions during relative sea-level fall. Geology, 43: 719-722. [文内引用:1]
[64] Nones M, Varrani A, Franzoia M, Di Silvio G. 2019. Assessing quasi-equilibrium fining and concavity of present rivers: a modelling approach. CATENA, 181: 104073. [文内引用:1]
[65] Nummedal D, Riley G W, Templet P L. 1993. High-resolution sequence architecture: a chronostratigraphic model based on equilibrium profile studies. In: Posamentier H W, Summerhayes C P, Haq B U, Allen G P(eds). Sequence Stratigraphy and Facies Associations. International Association of Sedimentologists Special Publication, 18: 55-68. [文内引用:2]
[66] Paola C, Parker G, Seal R, Sinha S K, Southard J B, Wilcock P R. 1992. Downstream fining by selective deposition in a laboratory flume. Science, 258(5089): 1757-1760. [文内引用:1]
[67] Parker G, Anderson A G. 1977. Basic principles of river hydraulics. Journal of the Hydraulics Division, 103: 1077-1087. [文内引用:2]
[68] Petter A L, Muto T. 2008. Sustained alluvial aggradation and autogenic detachment of the alluvial river from the shoreline in response to steady fall of relative sea level. Journal of Sedimentary Research, 78(2): 98-111. [文内引用:1]
[69] Porebski S J, Steel R J. 2006. Deltas and sea-level change. Journal of Sedimentary Research, 76(3): 390-403. [文内引用:1]
[70] Posamentier H W, Vail P R. 1988. Eustatic controls on clastic deposition Ⅱ—sequence and systems tract models. In: Wilgus C K, Hastings B S, Kendall C G St C, Posamentier H W, Ross C A, van Wagoner J C(eds). Sea Level Changes: An Integrated Approach. SEPM(Society of Economic Paleontologists and Mineralogists)Special Publication, 42: 125-154. [文内引用:9]
[71] Posamentier H W, Jervey M T, Vail P R. 1988. Eustatic controls on clastic deposition I—conceptual framework. In: Wilgus C K, Hastings B S, Kendall C G St C, Posamentier H W, Ross C A, van Wagoner J C(eds). Sea Level Changes: An Integrated Approach. SEPM(Society of Economic Paleontologists and Mineralogists)Special Publication, 42: 110-124. [文内引用:1]
[72] Posamentier H W, Allen G P, James D P, Tesson M. 1992. Forced regressions in a sequence stratigraphic framework: concepts, examples, and exploration significance. AAPG Bulletin, 76: 1687-1709. [文内引用:1]
[73] Posamentier H W, Allen G P. 1999. Siliciclastic sequence stratigraphy. Concepts and Applications: SEPM, Concepts in Sedimentology and Paleontology, 7, 210Tulsa, Okla. [文内引用:2]
[74] Schumm S A. 1993. River response to baselevel change: implications for sequence stratigraphy. The Journal of Geology, 101(2): 279-294. [文内引用:6]
[75] Shanley K W, McCabe P J. 1994. Perspectives on the sequence stratigraphy of continental strata. AAPG Bulletin, 78: 544-568. [文内引用:4]
[76] Sinha S K, Parker G. 1996. Causes of concavity in longitudinal profiles of rivers. Water Resources Research, 32: 1417-1428. [文内引用:1]
[77] Sømme T O, Helland -Hansen W, Martinsen O J, Thurmond J B. 2009. Relationships between morphological and sedimentological parameters in source-to-sink systems: a basis for predicting semi-quantitative characteristics in subsurface systems. Basin Research, 21(4): 361-387. [文内引用:1]
[78] Strong N, Paola C. 2008. Valleys that never were: time surfaces versus stratigraphic surfaces. Journal of Sedimentary Research, 78(8): 579-593. [文内引用:1]
[79] Swenson J B. 2005. Relative importance of fluvial input and wave energy in controlling the timescale for distributary-channel avulsion. Geophysical Research Letters, 32: L23404. [文内引用:2]
[80] Swenson J B, Muto T. 2007. Response of coastal plain rivers to falling relative sea-level: allogenic controls on the aggradational phase. Sedimentology, 54(1): 207-221. [文内引用:1]
[81] Swenson J B, Voller V R, Paola C, Parker G, Marr J G. 2000. Fluvio-deltaic sedimentation: a generalized Stefan problem. European Journal of Applied Mathematics, 11: 433-452. [文内引用:2]
[82] Swenson J B, Paola C, Pratson L, Voller V R, Murray A B. 2005. Fluvial and marine controls on combined subaerial and subaqueous delta progradation: morphodynamic modeling of compound-clinoform development. Journal of Geophysical Research, 110: F02013 [文内引用:1]
[83] Ta T K O, Nguyen V L, Tateishi M, Kobayashi I, Tanabe S, Saito Y. 2002. Holocene delta evolution and sediment discharge of the Mekong River, southern Vietnam. Quaternary Science Reviews, 21: 1807-1819. [文内引用:2]
[84] Ta T K O, Nguyen V L, Tateishi M, Kobayashi I, Saito Y. 2005. Holocene delta evolution and depositional models of the Mekong River Delta, southern Vietnam. In: Giosan L, Bhattacharya J P(eds). River Deltas: Concepts, Models, and Examples. SEPM(Society for Sedimentary Geology)Special Publication, 83: 453-466. [文内引用:1]
[85] Tamura T, Saito Y, Sieng S, Ben B, Kong M, Sim I, Choup S, Akiba F. 2009. Initiation of the Mekong River delta at 8 ka: evidence from the sedimentary succession in the Cambodian lowland . Quaternary Science Reviews, 28: 327-344. [文内引用:1]
[86] Tamura T, Saito Y, Nguyen V L, Ta T K O, Bateman M D, Matsumoto D, Yamashita S. 2012. Origin and evolution of interdistributary delta plains: insights from Mekong River delta. Geology, 40: 303-306. [文内引用:1]
[87] Thorne J A, Swift D J P. 1991. Sedimentation on continental margins, Ⅱ: Application of the regime concept. In: Swift D J P, Oertel G F, Tillman R W, Thorne J A(eds). Shelf Sand s and Sand stone Bodies: Geometry, Facies and Distribution. International Association of Sedimentologists Special Publication, 14: 33-58. [文内引用:1]
[88] Vail P R, Mitchum Jr. R M, Thompson III S. 1977. Seismic stratigraphy and global changes of sea level, part 3: relative changes of sea level from coastal onlap. In: Payton C E(ed). Seismic Stratigraphy: Applications to Hydrocarbon Exploration. American Association of Petroleum Geologists Memoir, 26: 63-81. [文内引用:1]
[89] Van Heijst M W I M, Postma G. 2001. Fluvial response to sea-level changes: a quantitative analogue, experimental approach. Basin Research, 13(3): 269-292. [文内引用:3]
[90] Van Wagoner J C, Posamentier H W, Mitchum R M J, Vail P R, Sarg J F, Loutit T S, Hardenbol J. 1988. An overview of the fundamentals of sequence stratigraphy and key definitions. In: Wilgus C K, Hastings B S, Kendall C G St C, Posamentier H W, Ross C A, van Wagoner J C(eds). Sea Level Changes: An Integrated Approach. SEPM(Society of Economic Paleontologists and Mineralogists)Special Publication, 42: 39-45. [文内引用:1]
[91] Van Wagoner J C, Mitchum R M, Campion K M, Rahmanian V D. 1990. Siliciclastic Sequence Stratigraphy in Well Logs, Cores, and Outcrops: concepts for High-Resolution Correlation of Time and Facies. AAPG Methods in Exploration Series, 7: 1-60. [文内引用:1]
[92] Wang J H, Muto T, Urata K, Sato T, Naruse H. 2019a. Morphodynamics of river deltas in response to different basin water depths: an experimental examination of the grade index model. Geophysical Research Letters, 46(10): 5265-5273. [文内引用:5]
[93] Wang J H, Tamura T, Muto T. 2019b. Construction and destruction of an autogenic grade system: the late Holocene Mekong River delta, Vietnam. Geology, 47(7): 669-672. [文内引用:7]
[94] Wang J H, Muto T. 2021. Autostratigraphic modelling of the growth of alluvial-shelf systems during steady base-level cycles: two-dimensional tank experiments. Sedimentology, 68(1): 135-167. [文内引用:5]
[95] Wheeler H E. 1964. Baselevel, lithosphere surface, and time-stratigraphy. Geological Society of America Bulletin, 75(7): 599-610. [文内引用:1]
[96] Wescott W A. 1993. Geomorphic thresholds and complex response of fluvial systems: some implications for sequence stratigraphy. AAPG Bulletin, 77(7): 1208-1218. [文内引用:1]