任昱霏, 闫建平, 王敏, 宋东江, 耿斌. (2025). 复杂碎屑岩粒度测井反演方法及在岩性精细识别中的应用* [J]. 古地理学报, 27(1): 240-255.
REN Yufei, YAN Jianping, WANG Min, SONG Dongjiang, GENG Bin. (2025). Particle size logging inversion method of deep complex clastic rock and its application in fine lithology identification[J]. Journal Of Palaeogeography, 27(1): 240-255.   
Doi: 10.7605/gdlxb.2024.06.069
Permissions
Copyright©2025, 《古地理学报》编辑部
版权所有.《古地理学报》编辑部
复杂碎屑岩粒度测井反演方法及在岩性精细识别中的应用*
任昱霏1,2, 闫建平1,2,3, 王敏4, 宋东江5, 耿斌4
1 西南石油大学地球科学与技术学院,四川成都 610500
2 天然气地质四川省重点实验室·西南石油大学,四川成都 610500
3 油气藏地质及开发工程全国重点实验室·西南石油大学,四川成都 610500
4 中国石化胜利油田分公司勘探开发研究院,山东东营 257015
5 山东瑞霖能源技术有限公司,山东东营 257000
通讯作者简介 闫建平,1980年生,理学博士,教授,博士生导师,主要从事测井地质学、非常规油气测井评价方面的教学与研究工作。E-mail: yanjp_tj@163.com。

第一作者简介 任昱霏,2001年生,西南石油大学在读硕士生,研究方向为测井地质学、岩石物理、数字信号处理与分析。E-mail: renyufei03@163.com。

收稿日期:2023-12-13 修回日期:2024-03-05
基金资助:*国家科技重大专项课题(编号: 2017ZX05072-002),国家自然科学基金项目(编号: 42372177)联合资助
摘要

南海西部Y盆地L地区中新统地层呈高温、超高压特征,钻井难度大、取心资料少,岩屑录井反映岩性的精度较低,难以满足岩性精细识别的要求。以Y盆地L地区黄流组二段深层复杂碎屑岩为例,首先,利用有限的壁心粒度分析、录井、测井等资料,优选出表征岩性的粒度参数: 粒度中值Md和对粒度变化敏感的自然伽马、密度、中子、声波时差、电阻率5条测井曲线,构建粒度中值Md-测井5变量数据集; 其次,采用K-MEANS聚类方法,将数据集根据“误差平方和与聚类数”最优关系划分成了4类(简称“粒度分类”),分类后优化了粒度中值Md与测井响应的相关性,且获得不同类别的测井响应特征和相应岩性类型; 然后,在实际井资料处理过程中,应用Fisher判别方程来判别未知深度点所属的粒度分类类型; 最后,建立粒度分类下基于XGBoost算法的粒度中值测井智能计算模型,依据不同岩性对应粒度中值的数值范围,实现了井筒剖面上根据测井反演粒度中值Md曲线进而达到岩性精细识别的目的。研究结果表明: L地区黄流组二段考虑粒径的差异将砂岩岩性划分为: 粉砂岩、细砂岩、中砂岩、粗砂岩,其中细砂岩和中砂岩是最主体发育的岩性,粒度中值Md与不同粒径岩性的关系最密切,是最能反映不同粒径岩性的粒度参数; 粒度分类后基于XGBoost算法的粒度中值测井智能计算模型预测效果优于多元回归预测模型,计算粒度中值与实测值的相关系数达0.9397,平均绝对误差MAE为0.0195 mm,平均相对误差MRE为17.52%。该模型是一种有效实现深层复杂碎屑岩岩性精细识别的方法,也为纵向剖面上沉积粒序分析和储层构型精细解释、有效性评价奠定了基础。

关键词: 南海; 中新统; 复杂岩性; 粒度中值; 测井; 反演; 机器学习; XGBoost算法
中图分类号:P631.8 文献标志码:A 文章编号:1671-1505(2025)01-0240-16
Particle size logging inversion method of deep complex clastic rock and its application in fine lithology identification
REN Yufei1,2, YAN Jianping1,2,3, WANG Min4, SONG Dongjiang5, GENG Bin4
1 School of Geoscience and Technology,Southwest Petroleum University,Chengdu 610500,China
2 Natural Gas Geology Key Laboratory of Sichuan Province-Southwest Petroleum University,Chengdu 610500,China
3 State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation-Southwest Petroleum University,Chengdu 610500,China
4 Institute of Exploration and Development,Shengli Oil Field,SINOPEC,Shandong Dongying 257015,China
5 Shandong Ruilin Energy Technology Co.,Ltd,Shandong Dongying 257000,China
About the corresponding author YAN Jianping,born in 1980,Ph.D., is a professor and doctoral supervisor. He is mainly engaged in teaching and research in logging geology and unconventional oil and gas logging evaluation. E-mail: yanjp_tj@163.com.

About the first author REN Yufei,born in 2001, is a masteral candidate at Southwest Petroleum University,with research interests in logging geology,rock physics,and digital signal processing and analysis. E-mail: renyufei03@163.com.

Fund:Co-funded by National Science and Technology Major Project(No. 2017ZX05072-002)and National Natural Science Foundation of China(No.42372177)
Abstract

The Miocene strata in the L area of the Y Basin in the western part of the South China Sea are characterised by high temperature and ultra-high pressure,which makes drilling difficult and core data rare. In addition, the accuracy of rock chip logging in reflecting lithology is relatively low,making it difficult to meet the requirements of fine identification of lithology. The deep clastic rocks in the second section of Huangliu Formation in the L area of Y basin are used in this study,firstly,using the limited data of core size analysis,rock chip logging and logging,we selected the particle size parameter characterizing lithology: median Md and five logging curves of natural gamma,density,neutron,acoustic time difference and resistivity which are sensitive to changes in the particle size,and constructed the data set of five variables of the median Md and logging,and then we used K-MEANS secondly,using K-MEANS clustering method,the dataset was divided into four classes according to the optimal relationship between “sum of error squares and the number of clusters”(referred to as “granularity classification”),which optimised the correlation between the median Md-granularity and the logging response,and obtained the logging response characteristics of the different classes and the corresponding lithological types. Then,in the actual well data processing process,Fisher's discriminant equation is applied to determine the type of particle size classification to which the unknown depth point belongs,and finally,the intelligent calculation model of median particle size logging based on XGBoost algorithm is established under the particle size classification,and based on the numerical range of median particle size corresponding to different lithologies,it realises the purpose of fine identification of lithology by inverting the median Md curve according to the logging on the wellbore profile. The purpose of fine identification of lithology is achieved by inverting the Md curve on the wellbore profile according to the logging.The results show that the sandstone lithology in the second section of Huangliu Formation in L area is divided into: siltstone,fine sandstone,medium sandstone and coarse sandstone considering the difference of grain size,among which the fine sandstone and medium sandstone are the most dominantly developed lithologies,and the median Md of grain size has the closest relationship with the lithology of different grain sizes,and it is the most reflective of the different grain sizes of lithologies;the intelligent calculation of the median Md of grain size logging model based on XGBoost algorithm is better than that of multiple regression algorithm after the classification of the grain sizes. The prediction effect of the model is better than that of the multiple regression prediction model,and the correlation coefficient between the calculated median particle size and the measured value reaching 0.9397,the average absolute error(MAE) is 0.0195,and the average relative error MRE is 0.1752. The model is an effective method for the fine identification of the lithology of the deep complex clastic rocks,and it also lays a foundation for sedimentary grain sequence analysis and fine interpretation of the reservoir configuration,and the evaluation of the validity on the vertical profile. It also lays the foundation for sedimentary grain sequence analysis,fine interpretation of reservoir configuration and validity evaluation in longitudinal section.

Key words: South China Sea; Miocene; complex lithology; median grain size; logging; inversion; machine learning; XGBoost algorithm

深层超深层已成为中国油气勘探的重要接替领域(Bloch et al., 2002; Xin et al., 2022), 其中南海西部Y盆地L地区深层碎屑岩储集层具有较大的勘探开发潜力(谢玉洪, 2011; 杨楷乐等, 2023)。相较于浅层, L地区黄流组深层储集层呈现高温、超高压及岩性复杂的特点(Yuan et al., 2017; 范彩伟等, 2022), 钻井难度大, 也不易全井段取心, 岩心收获率低。具有优势的是录井资料丰富, 但岩屑录井反映岩性的精度较低, 通常一整段(> 1.0 m)显示为同一种岩性, 导致垂向剖面上的岩性细分存在较大的误差。为了有效降低勘探开发成本, 提高岩性识别精度, 采用有限的壁心描述、粒度分析资料, 结合测井曲线实现粒度参数的反演, 进而利用计算的粒度参数对不同粒径岩性进行精细识别, 成为储集层精细刻画与表征的重要手段。

粒度资料在岩性分析中被广泛应用, 粒度也是岩石物理性质评价的关键评价参数。粒度参数计算方法主要为图解法和矩值法(Folk and Ward, 1957; Friedman and Johnson, 1982; McManus, 1988)。粒度中值Md为粒度累积曲线50%处所对应的粒径值(谢晓庆等, 2022), 作为一种重要的粒度参数, 在刻画碎屑岩岩性上比其他粒度参数更具有代表性。赵军等(2016)在分析岩性指数参数与粒度中值关系基础上, 利用自然伽马、电阻率曲线和岩性指数M、N建立了基于多参数的粒度中值计算模型。Faga和Oyeneyin(2000)、刘珊珊和汪志明(2022)基于机器学习和神经网络技术, 采用多条测井曲线建立了纵向粒度中值曲线预测模型。杨宁等(2012)依据自然伽马曲线, 采用二进制小波变换方法计算了粒度中值等粒度参数。吴进波等(2022)通过核磁和粒径对应关系建立了核磁测井计算粒度参数模型。以上方法均是通过测井资料求得粒度中值, 但上述方法均存在一定程度的不足, 多元回归建立计算模型的精度往往较低; 机器学习直接将粒度参数作为输入, 忽略了测井曲线与粒度参数关系背后的地质意义; 依据小波变换数学方法建立模型相对简单与实际地层情况存在差异, 且仅采用GR曲线预测粒度变化是有明显局限性(Hurst, 1990); 核磁T2谱和粒度之间对应关系复杂, 无法实现L地区的复杂岩性的精细判识(Conroy, 2010)。

针对Y盆地L地区新近系黄流组二段存在不同粒径砂岩的特点, 利用壁心描述、录井岩性、粒度分析及测井等资料, 筛选出更能反映不同粒径岩性的粒度参数: 粒度中值Md, 刻度测井提取出自然伽马(GR)、电阻率(Rd)、密度(DEN)、中子孔隙度(CNL)、声波时差(AC)作为粒度中值敏感的5条曲线, 分析不同岩性的粒度中值数值范围及测井响应特征, 利用主成分分析方法结合K-MEANS聚类方法实现“ 粒度中值Md-测井5变量” 数据集的分类(简称“ 粒度分类” ), 得到4个类型的粒度中值与测井响应对应关系, 进一步训练4种分类后的基于XGBoost算法的粒度中值计算模型。在实际井资料处理过程中, 采用Fisher判别方程对井筒剖面上的未知深度点进行类型判别, 然后带入对应基于XGBoost算法的粒度中值测井智能计算模型进行粒度中值计算, 即可得到1条类似连续测井曲线的粒度中值曲线, 该模型的预测效果优于多元回归模型, 粒度中值预测值与实际测试值相关系数高达0.9397。最终, 依据不同岩性对应粒度中值范围, 实现了井筒剖面上不同粒径岩性的精细识别, 通过与壁心岩性描述、成像测井图像等对比检验, 证明了粒度中值测井智能计算模型的精确性与有效性, 实质性解决了L地区复杂碎屑岩岩性精确识别困难的问题, 也为进一步开展沉积粒序分析、储集层构型精细解释和有效性评价提供了依据。

1 地质概况

Y盆地位于南海海域西部大陆边缘, 受到欧亚、印澳和太平洋三大板块的相互作用, 是一个大型新生代走滑伸展盆地(任建业和雷超, 2011), 面积约为11.3× 104 km2。

盆地可划分为YD斜坡、YX斜坡和中央坳陷3个一级构造单元, 中央坳陷内有临高凸起和底辟构造带2个正向构造单元, 底辟构造带又被称作“ 中央底辟带” (段威等, 2015)。盆内地层自下而上为新近系中新统的三亚组(N1s)、梅山组(N1m)、黄流组(N1h)和上新统的莺歌海组(N2y), 第四系乐东组(Q1)(毛倩茹等, 2022)。L地区(图1-a)构造位置处于Y盆地中央底辟构造带与YD斜坡之间, 研究层位是新近系中新统黄流组二段(图1-b)。勘探实践中, 将上新统莺歌海组二段上部— 第四系乐东组储盖组合划分为浅层, 埋藏相对较浅, 压力系数介于1.0~1.5之间, 属于常压— 压力过渡带领域; 将梅山组— 黄流组储盖组合划分为中深层, 埋藏较深, 地温梯度超过45℃/km, 压力系数大于1.8, 属于高温、超压区域(李超等, 2021)。L地区黄流组二段主体为峡谷水道沉积(刘为等, 2020), 砂体主要岩性为中、细砂岩, 水道底部含部分粗砂岩(尤丽等, 2021), 砂体岩性在纵向上变化快, 岩性精细识别困难。

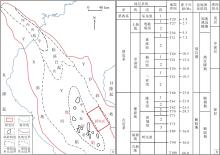图1 Y盆地构造分区图(a)与地层柱状图(b)(据杨计海等, 2018; 李伟等, 2020; 有修改)Fig.1 Structural zoning map(a)and stratigraphic histogram(b)of Y Basin(modified from Yang et al., 2018; Li et al., 2020)

2 岩性和粒度及测井响应特征
2.1 岩性和粒度特征

粒度参数是分析岩石结构和岩性的重要参数, 目前广泛使用的粒度参数有粒度中值Md、平均粒径Mz、分选系数So、偏度Sk、峰度K等(谭增驹等, 1995)。平均粒径Mz和粒度中值Md均表现岩石粒度分布的集中趋势, 表1针对164个样本点的粒度参数及其对应测井曲线值做皮尔逊相关性分析, 粒度中值与测井曲线的相关系数值更大, 因此, 采用粒度中值Md研究碎屑岩岩性比平均粒径Mz更客观、更具适应性。

表1 Y盆地L地区新近系黄流组粒度参数与测井曲线的Pearson相关系数 Table 1 Pearson correlation coefficient between grain size parameters and logging curves for the Neogene Huangliu Formation in L area of Y Basin

L地区黄流组二段深层复杂碎屑岩储集层4口井取心岩性描述共204个样本点统计显示(图2-a), 岩性整体偏细, 发育的岩性有粉砂岩、细砂岩、中砂岩、含砾中砂岩、粗砂岩, 结合矿物组分还发育灰质粉砂岩、灰质细砂岩、灰质中砂岩。另外, 目的层8口井粒度分析资料共237个样本点统计显示(图2-b), 粒度中值Md最小值0.004 mm, 最大值0.440 mm, 平均为0.180 mm, 分布范围集中在0~0.250 mm, 粒度中值Md总体分布范围较窄, 数值也较小。上述已知岩性的种类丰富, 考虑到粒径的分布范围、粒径与岩性的关系以及涵盖岩性的完整性, 在实际处理中, 将岩性类型归纳为粉砂岩、细砂岩、中砂岩和粗砂岩, 粉砂岩、粗砂岩的占比非常少, 即细砂岩和中砂岩是最主体发育的岩性, 若能通过测井曲线数据准确反演粒度中值Md, 进而区分细砂岩和中砂岩这2种主体岩性, 对精细划分地层岩性剖面非常的重要。

图2 Y盆地L地区新近系黄流组岩性分布(a)和粒度中值分布(b)Fig.2 Lithology distribution(a)and median grain size distribution(b)for the Neogene Huangliu Formation in L area of Y Basin

基于4种岩性粒度中值Md的分布特征, 可以明确粒度中值Md划分不同粒径岩性的标准。以L地区8口井取心237个样本粒度中值数据及对应的岩性描述为基础, 参考粒径岩石定名规则(朱筱敏, 2008), 建立了粒度中值Md与岩性的关系(图3), 可将岩性按粒度中值Md范围做进一步标定: 粉砂岩, Md≤ 0.06 mm; 细砂岩, 0.06 mm< Md≤ 0.19 mm; 中砂岩, 0.19 mm< Md≤ 0.32 mm, 由于粗砂岩的粒度样本点少, 给出一个粗略范围: 粗砂岩, 0.32 mm≤ Md< 0.5 mm。

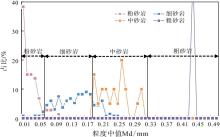图3 Y盆地L地区新近系黄流组粒度中值Md与岩性对应关系Fig.3 Corresponding relationship between median grain size and lithology for the Neogene Huangliu Formation in L area of Y Basin

电成像测井图像资料同样反映了重力流峡谷水道整体岩性细且纵向变化快的特征, 采用取心岩性描述刻度电成像测井图像, 建立4种不同粒径岩性对应的静态FMI图像图版(图4), 以用于后续粒度中值计算模型反演粒度中值曲线进而识别岩性的精确性验证。电成像测井(FMI)分辨率高且图像直观(罗歆等, 2023), 可反映岩性、结构、构造和沉积韵律性等特征(闫建平等, 2011)。静态FMI图像的明暗可反映岩性的粗细, 在复杂碎屑岩剖面中, 粉砂岩通常由于电阻率较低, 静态FMI图像显示暗棕色, 随着粒径增大, 电阻率值也增大, 图像颜色变亮, 粗砂岩图像整体呈现亮黄色。

图4 Y盆地L地区新近系黄流组不同粒径岩性与FMI静态图像颜色对应关系Fig.4 Corresponding relationship between lithology of different particle sizes and FMI static image color for the Neogene Huangliu Formation in L area of Y Basin

2.2 不同粒度碎屑岩测井响应特征

实现粒度参数纵向预测必须借助各类测井曲线, 影响测井曲线的因素较多, 曲线变化与岩石成分、岩石粒度、孔隙结构、孔隙流体性质等因素有关。在岩石成分差别较小的情况下, 岩石粒度是导致测井曲线变化的关键因素之一(罗利等, 2007)。自然伽马主要由泥质含量决定, 自然伽马数值越高, 泥质含量越高, 反映粒度越小。中子孔隙度对岩石中束缚水含量比较敏感, 粒度越小, 束缚水含量越高, 中子孔隙度越大。电阻率受孔隙体积差异影响, 粒度越小, 束缚水含量就高, 电阻率越小; 粒度越大, 孔隙复杂, 粒度与电阻率相关性变差, 只有消除孔隙度贡献因素后才能体现电阻率对粒度的变化(赵军等, 2013)。密度与粒度具有负相关性, 往往密度越高, 压实程度越强, 孔隙度越小, 反映粒度越小。砂岩一般情况下声波时差曲线值显示低值。L地区黄流组广泛发育碳酸盐胶结物(吴仕玖等, 2019), 粒度越大, 填隙物相对越多, 碳酸盐胶结物越多, 砂岩越致密, 声波时差值越小。

从8口井的粒度中值资料与其对应的测井曲线值的164个样本点绘制的散点图(图5)可以看出, 粒度中值Md和自然伽马(GR)、电阻率(Rd)、密度(DEN)、中子孔隙度(CNL)、声波时差(AC)的变化趋势及其相关程度。随着粒度中值Md的增大, GR、AC、CNL、DEN减小, Rd增大。

图5 Y盆地L地区新近系黄流组粒度中值和测井变量的关系Fig.5 Relationship between median grain size and logging for the Neogene Huangliu Formation in L area of Y Basin

对上述粒度分析命名4类岩性的常规测井数据做二维交会(GR与Rd、AC与CNL)分析(图6), 可以看出, 不同类型的岩性测井响应特征有差异, 但取值区域也存在一定的重叠, 重叠的主要原因在于: 从测井原理来讲, 曲线之间本身存在信息冗余; 不同井的环境不同, 实际测量过程的干扰因素不同, 导致同一口井存在相关性, 不同井之间存在差异性(马峥等, 2017)。二维交会图虽反映出测井曲线之间的相关性和模糊性(张涛和莫修文, 2007), 但无法将不同岩性进行准确区分。

图6 Y盆地L地区新近系黄流组4类岩性测井二维交会图Fig.6 Two-dimensional crossplot of four types of lithology logging for the Neogene Huangliu Formation in L area of Y Basin

3 粒度测井反演方法及岩性判识
3.1 聚类分析下的“ 粒度中值— 测井数据集” 分类

由于不同粒度的岩性表现出的测井响应复杂, 因此, 考虑先进行粒度中值— 测井响应数据集的分类, 试图基于分类来优化粒度中值与测井响应的相关关系。粒度中值敏感测井曲线反应的信息存在相关性, 对聚类产生干扰, 可先采用主成分分析方法消除测井曲线之间的重叠信息, 突出粒度中值信息。主成分分析法是一种考察变量之间相关性的数学统计方法, 其核心思想是将多个存在相关关系的特征变量, 保留为数量更少、保持原有信息量的综合变量(张强等, 2022)。利用主成分法分析粒度中值测井响应, 可将原始的5个测井变量转化为独立的综合测井变量, 消除冗余信息对聚类的影响, 突出岩性粒度中值特征。

采用与粒度中值相关的5条测井曲线变量建立样本库(数据集), 由于各曲线变量的量纲不同, 在数量级上也存在较大差异, 因此对数据进行标准化, 标准化处理公式为(刘毅等, 2017):

x'ij=xij-x-jSj

其中, x-j为样本库中第j列的平均值; Sj为样本库第j列的标准差。

再计算样本的相关系数矩阵R(表2), 求出矩阵R的特征根和特征向量, 得到各主成分的特征向量和方差贡献率(表3)。

表2 Y盆地L地区新近系黄流组主成分分析相关系数矩阵 Table 2 Correlation coefficient matrix of principal component analysis for the Neogene Huangliu Formation in L area of Y Basin
表3 Y盆地L地区新近系黄流组主成分分析特征值及特征向量计算结果 Table 3 Principal component analysis eigenvalue and eigenvector calculation results for the Neogene Huangliu Formation in L area of Y Basin

每个独立的主成分变量都能通过不同贡献率来反映所携带信息的多少, 当变量的维数增加, 贡献率会减少, 也会增加分析问题的复杂性(张焱等, 2015)。一般认为累积方差贡献率大于85%前的主成分变量可以反映原始样本的绝大部分信息(梁则亮等, 2022), 此时的主成分个数为最佳变量个数。由表3可知, 当选取3个主成分(Y1、Y2和Y3)时, 累积方差贡献率大于85%, 因此将提取的主成分数量确定为3, 并采用Y1、Y2、Y3代替对粒度中值敏感的5条测井曲线变量作为聚类输入。

聚类分析是指将数据样本进行分类, 保证其同一簇内数据间差异性最小, 不同簇数据间差别最大。考虑到K-MEANS聚类方法不但具有高效执行率, 还能决定最优聚类数, 因此选取该方法对粒度中值— 测井变量数据集的聚类数进行优选。K-MEANS聚类的核心思想是: 从样本集中随机挑选k个初始聚类中心Ci(1≤ i≤ k), 计算其余样本到聚类中心Ci的欧式距离, 找出离目标样本最近的聚类中心, 将样本划分到Ci所对应的簇内。计算每个簇中样本的平均值作为新的聚类中心, 进行下一次迭代, 直到聚类中心不再改变或满足最大迭代次数后输出聚类结果(杨俊闯和赵超, 2019)。

整个样本集的“ 误差平方和” SSE是判断聚类效果好坏的标准(成卫青和卢艳红, 2015)。K-MEANS聚类随着簇数k的增加, 其样本划分会更加精细, SSE值会逐渐变小, 当k值超过某一“ 肘点” , SSE会趋于平缓, 增加聚类数将失去意义, 因此“ 肘点” 对应的k值为该样本集的最优簇数。针对8口井164组粒度中值— 测井响应(5条曲线变量)样本数据集, 提取3个主成分变量作为输入进行聚类, 得到“ 簇数误差平方和” SSE与k值的变化关系(图7), 当聚类数超过4时, SSE趋于平缓, 因此选择4为最优聚类数。

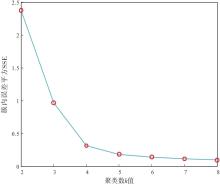图7 Y盆地L地区新近系黄流组k值和SSE的关系Fig.7 Relationship between k-value and SSE for the Neogene Huangliu Formation in L area of Y Basin

得到4个类别的粒度中值特征和测井响应规律(表4), 从第1类到第4类, 粒度中值Md由小变大, 自然伽马GR、密度DEN、中子CNL值由大变小, 电阻率Rd值由小变大。其中, 第3类电阻率值明显高于其他3类, 与第4类相比, 第3类的中子值偏小。L地区中新统黄流组二段碳酸盐胶结物普遍发育, 存在灰质砂岩, 灰质砂岩特征较一般砂岩呈现“ 三低两高” (较低自然伽马值、低中子值、低声波时差值、高电阻率值、高密度值)的测井响应特征(赵笑笑等, 2022), 与第3类的测井曲线特征相符, 从取心描述、岩矿测试和录井岩性分析均证明了第3类为灰质较重的砂岩。

表4 Y盆地L地区新近系黄流组不同类别的粒度特征和测井响应参数 Table 4 Different types of grain size characteristics and logging response parameters for the Neogene Huangliu Formation in L area of Y Basin

利用上述164组粒度中值— 测井响应(5条曲线变量)样本数据, 分析不同聚类类别和岩性的对应关系(图8)显示, 分类可对岩性进行粗略划分。

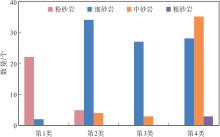图8 Y盆地L地区新近系黄流组4类岩性与聚类类别的对应关系Fig.8 Corresponding relationship between four types of lithology and clustering categories for the Neogene Huangliu Formation in L area of Y Basin

第1类以粉砂岩为主, 第2类、第3类均以细砂岩为主, 第4类以细砂岩、中砂岩为主, 由于样本点较少, 仅含少量粗砂岩。尽管第2、3类均属于细砂岩, 但电阻率值相差较大。通过分类减小了测井曲线的分布范围(表4), 从而优化了粒度中值Md与5条测井曲线的相关性, 有助于建立精度更高的粒度中值测井反演模型。

3.2 测井剖面上“ 聚类类型” 的Fisher判别

Fisher判别分析法是根据已知的样本类别数据集对未知样本进行分析识别, 并判断其所属类别。前述通过聚类方法将已知粒度中值— 测井响应(5条曲线变量)样本数据划分为4类, 但无法实现未知井筒剖面上任一深度样本点的判别, Fisher判别具有对未知样本判别其类型准确率高的优点(黄仁东等, 2011), 通常采用Fisher判别方程能很好地对未知样本进行预测。Fisher分析判别的基本思想是利用投影技术, 将多维空间中的点投影到一维方向, 再根据未知样本点与已知样本类型的亲疏程度判别其类别(田艳等, 2010)。因此, 仍然针对上述164组粒度中值— 测井响应(5条曲线变量)样本数据求得判别函数为:

F1=-0.0719× GR+0.0074× Rd-0.6627× DEN+0.0129× CNL+0.0064× AC+6.1172

F2=0.0326× GR+0.105× Rd+0.5282× DEN+0.0075× CNL+0.0016× AC-5.5673

F3=-0.009× GR+0.0186× Rd-0.7833× DEN-0.0231× CNL+0.0703× AC-2.6305

F4=0.0307× GR-0.0025× Rd-4.984× DEN-0.1554× CNL+0.0064× AC+10.848

F5=-0.005× GR-0.0156× Rd+5.3668× DEN-0.1113× CNL+0.0168× AC-13.2858

Fisher判别法的步骤为: 第一步, 计算该样本与其余各样本投影的马氏距离; 第二步, 比较马氏距离的大小来判断该样本属于哪一类别。由表5可知第一、第二判别函数其累积贡献率为99.01%> 85.0%, 因此, 采用第一、第二判别方程结合马氏距离就可实现未知样本的准确判别。

表5 Y盆地L地区新近系黄流组Fisher判别特征值及贡献率计算结果 Table 5 Fisher discriminant eigenvalue and contribution rate calculation results for the Neogene Huangliu Formation in L area of Y Basin

将所有训练样本看作待判样本, 带入判别方程F1、F2, 通过判断F1、F2到已知类别中心点的马氏距离判断其类别的过程称为回代判别(回判)。Fisher判别也具有对已知样本点回代判别准确率高的优点, 通过回判准确率可以检验该判别的准确性(表6), 可以看出各类别回判准确率均高于90%, 证明该判别模型的准确性高。

表6 Y盆地L地区新近系黄流组Fisher回代判别准确率分析 Table 6 Fisher back substitution discriminant accuracy analysis for the Neogene Huangliu Formation in L area of Y Basin
3.3 粒度中值测井智能计算模型

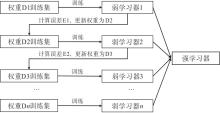
前述已知, 不管是岩性还是反映岩性的粒度中值参数, 测井曲线都有一定的研判性, 但是也存在很大的多解性, 而机器学习/深度学习等人工智能方法是解决数据多解性提高计算或判识准确率的重要途径。极致梯度提升决策树XGBoost(Extreme Gradient Boosting), 是Chen和Guestrin(2016)在当前流行的梯度提升决策树GBDT(Gradient Boosting Decision Tree)算法优化基础上提出的一种旨在高效、灵活且可移植性强的机器学习算法。XGBoost算法通过对多个弱分类器设置权重后组合成一个强分类器后输出, 每一个弱分类器由每一轮迭代获得的损失函数沿着梯度方向降获得, 其原理流程如图9所示。

图9 XGBoost算法思想Fig.9 Algorithm idea of XGBoost

相比于GBDT算法, XGBoost算法通过自动采用CPU进行多线程并行运算来提高算法运算速度, 将Taylor展开的二阶导作为损失函数, 二阶信息具有可以描述梯度变化方向、梯度下降更快、方向更加准确等优点, 从而提高模型预测精度, 且在损失函数增加了“ 正则项” , 降低了模型的复杂度(孙予舒等, 2020)。XGBoost预测模型可用公式表示为(李建平等, 2022):

F(xi)=f0(xi)+∑k=1KX∑j=1TKwj, k×η

其中, f0(xi)为弱学习器, xi为第i个样本, k为循环次数, j为第k次迭代的CART叶节点个数, η 为学习率, wj, k为第j次迭代的第j叶节点区域的所有样本的拟合值。

提取Y盆地L地区黄流组二段粒度中值Md-测井5变量数据集164个样本点, 随机选取样本库的70%作为训练数据集, 30%作为测试数据集, 采用XGBoost算法建立粒度中值测井Fisher分类判别的智能计算模型。根据上述研究, 将分类后的粒度中值Md、自然伽马(GR)、电阻率(Rd)、密度(DEN)、中子孔隙度(CNL)、声波时差(AC)作为单独的4个样本库输入, 设置迭代次数为100, 学习率为0.3, 树的最大深度为6, 采用均方根误差RMSE作为误差函数分析误差。得到4类的最终训练模型, 为了Fisher判别分类后基于XGBoost算法的粒度中值测井智能计算模型的准确性, 将多元回归计算模型与该模型进行对比验证其优越性。

采用数据集164个样本点, 其中70%作为训练数据集, 30%作为测试数据集, 将不同模型的粒度中值计算值与测试集中壁心实测值进行对比, 结果表明: 不进行粒度中值分类的多元回归方法计算精度最低, 数据点大多偏离45° 线(图10-a), 平均绝对误差MAE为0.0358 mm, 平均相对误差MRE为37.75%; 进行粒度中值分类的多元线性回归模型计算精度有所提高, 相关系数增大, 与45° 线夹角变小(图10-b), 平均绝对误差MAE为0.0278 mm, 平均相对误差MRE为24.83%; 进行粒度中值分类后基于XGBoost算法的智能计算模型预测精度最高, 其相关系数达0.9397, 平均绝对误差MAE为0.0195 mm, 平均相对误差MRE为17.52%, 预测粒度中值与实际粒度中值接近, 数据点均匀分布在45° 线附近(图10-c)。

图10 Y盆地L地区新近系黄流组未进行粒度中值分类的多元回归模型(a)、粒度中值分类的多元回归模型(b)和粒度中值分类后基于XGBoost智能算法模型(c)Fig.10 Multiple regression model without granularity median classification(a), multiple regression model of granularity median classification(b), and XGBoost intelligent algorithm model based on granularity median classification(c)for the Neogene Huangliu Formation in L area of Y Basin

以L地区L-1井黄流组二段为例(图11), 采用粒度中值分类的XGBoost智能计算模型与进行粒度分类的多元回归模型进行粒度中值曲线计算, 第7道为多元回归模型计算结果与粒度中值实测值对比, 第8道为XGBoost智能模型计算结果与粒度中值实测值对比, 2种模型的计算结果对比发现, 在具体实测深度点上, XGBoost模型的计算值与粒度中值实测值的吻合效果优于多元回归模型, 且高频滤波后的粒度中值曲线消除了不合理的一些毛刺之处, 更趋于平缓, 表明基于XGBoost算法的粒度中值测井智能计算模型具有良好的学习效率, 预测结果有较高的精度, 能够反演获得准确的粒度中值曲线, 进而实现井筒剖面上的岩性精细识别。

图11 Y盆地L地区新近系黄流组L-1井XGBoost智能计算模型与多元回归计算模型对比效果Fig.11 Comparison effect of XGBoost intelligent calculation model and multiple regression calculation model in Well L-1 of the Neogene Huangliu Formation in L area of Y Basin

4 基于粒度中值曲线恢复精细岩性剖面
4.1 基于粒度中值曲线的精细岩性识别流程

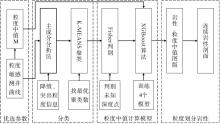
根据不同粒径岩性的粒度中值划分范围、粒度中值聚类分类和XGBoost算法, 建立基于粒度中值曲线精细识别岩性的步骤与流程。

其具体方法流程如图12所示, 5条粒度敏感曲线作为输入, 首先采用主成分分析法、K-MEANS聚类法等对粒度中值— 测井响应(5条曲线变量)样本数据集划分为4类, 以5条敏感曲线为输入, 通过Fisher判别方程来判别未知深度点所属的分类类型, 采用对应类别的XGBoost算法测井智能计算模型, 最终求出一条连续的粒度中值曲线, 进而通过不同粒径岩性的粒度中值范围判断岩性, 得到井筒目的层连续精细的岩性剖面。

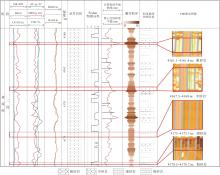
图12 Y盆地L地区新近系黄流组粒度精细识别岩性流程Fig.12 Grain size fine identification lithology process for the Neogene Huangliu Formation in L area of Y Basin

4.2 实例分析及应用

以L地区L-1井黄流组二段为例, 在连续测井剖面上采用XGBoost模型计算粒度中值曲线并进一步划分岩性。图13为研究区该井粒度计算及岩性识别效果图, 第7道为录井岩性, 第8道为Fisher判别分类, 第9道为本文粒度分类的基于XGBoost算法的粒度中值计算模型计算粒度曲线与壁心实际粒度对比, 第11道为根据粒度中值曲线划分岩性。第9道计算粒度中值Md与实际粒度中值Md吻合较好且误差值小, 第7道录井岩性表明该段为大段中砂岩, 而通过第11道粒度中值划分岩性分析表明该段4类砂岩岩性均存在且岩性变化复杂, 粒度中值曲线识别出的不同岩性与颜色标定后的电成像岩性对比, 4种岩性对应好, 证实该模型进行粒度实现精细识别岩性的可行性。

图13 Y盆地L地区新近系黄流组L-1井粒度划分岩性成果Fig.13 Lithology result of Well L-1 grain size division for the Neogene Huangliu Formation in L area of Y Basin

5 结论

1)Y盆地L地区新近系黄流组二段主体为峡谷水道沉积, 砂体岩性在纵向、横向上变化快, 岩性精细识别难度大, 根据不同的粒径范围, 砂岩岩性可划分为: 粉砂岩、细砂岩、中砂岩、粗砂岩, 其中细砂岩和中砂岩是最主体发育的岩性, 粒度中值参数与不同粒径岩性的关系最密切, 是最能反映不同粒径岩性的粒度参数, 厘定了不同粒径岩性的粒度中值参数范围界限。

2)粒度中值变化敏感的测井曲线有自然伽马、密度、中子孔隙度、声波时差、电阻率, 基于粒度中值Md-测井5变量数据库集, 采用K-MEANS聚类方法, 将数据库根据“ 样本集误差平方和与聚类数” 最优关系划分成了4类(简称“ 粒度分类” ), 分类后优化了粒度中值Md与测井响应的相关性。

3)实际井资料处理过程中, 应用Fisher判别方程可判别未知深度点所属的粒度分类类型, 进而建立了粒度分类后基于XGBoost算法的粒度中值测井智能计算模型, 实现了井筒剖面上依据测井反演粒度中值Md曲线, 借助不同岩性对应的粒度中值范围, 达到了Y盆地L地区黄流组岩性精细识别的目的, 也为纵向剖面上的沉积学分析和储层构型精细解释、有效性评价奠定了基础。

(责任编辑 郑秀娟; 英文审校 赖锦)

参考文献
[1] 成卫青, 卢艳红. 2015. 一种基于最大最小距离和SSE的自适应聚类算法. 南京邮电大学学报(自然科学版), 35(2): 102-107.
[Cheng W Q, Lu Y H. 2015. Adaptive clustering algorithm based on maximum and minimum distances, and SSE. Journal of Nanjing University of Posts and Telecommunications(Natural Science Edition), 35(2): 102-107] [文内引用:1]
[2] 段威, 罗程飞, 刘建章, 田金强, 吕波, 丁亮. 2015. 莺歌海盆地LD区块地层超压对储层成岩作用的影响及其地质意义. 地球科学, 40(9): 1517-1528.
[Duan W, Luo C F, Liu J Z, Tian J Q, Lü B, Ding L. 2015. Effect of overpressure formation on reservoir diagenesis and its geological significance to LD block of Yinggehai Basin. Earth Science, 40(9): 1517-1528] [文内引用:1]
[3] 范彩伟, 刘爱群, 吴云鹏, 侯静娴. 2022. 莺歌海盆地乐东10区新近系黄流组储层天然气充注与超压演化史. 石油与天然气地质, 43(6): 1370-1381.
[Fan C W, Liu A Q, Wu Y P, Hou J X. 2022. Gas charging and overpressure evolution history of the Neogene Huangliu Formation reservoir in Ledong 10 area, Yinggehai Basin. Oil & Gas Geology, 43(6): 1370-1381] [文内引用:1]
[4] 黄仁东, 韩明, 张小军, 张海彬, 金浩, 华正阳. 2011. 基于Fisher判别法岩溶塌陷倾向性等级分类预测. 中国安全科学学报, 21(9): 70-76.
[Huang R D, Han M, Zhang X J, Zhang H B, Jing H, Hua Z Y. 2011. Classification prediction of karst collapse tendency level based on fisher discriminant analysis method. China Safty Science Journal, 21(9): 70-76] [文内引用:1]
[5] 李超, 罗晓容, 范彩伟, 张立宽, 刘爱群, 李虎, 李俊. 2021. 莺歌海盆地乐东斜坡区乐东A构造储层超压形成机制及其对天然气成藏的启示. 地质科学, 56(4): 1034-1051.
[Li C, Luo X R, Fan C W, Zhang L K, Liu A Q, Li H, Li J. 2021. Generation mechanism of overpressure and its implication for natural gas accumulation in Miocene reservoir in Ledong A structrure, Ledong slope, Yinggehai Basin. Chinese Journal of Geology(Scientia Geologica Sinica), 56(4): 1034-1051] [文内引用:1]
[6] 李建平, 张小庆, 李莹. 2022. 基于XGBoost的低渗油田储层粒度预测. 计算机系统应用, 31(2): 241-245.
[Li J P, Zhang X Q, Li Y. 2022. Prediction of reservoir grain size in low permeability oilfield based on XGBoost. Computer Systems & Applications, 31(2): 241-245] [文内引用:1]
[7] 李伟, 刘平, 艾能平, 邵远, 侯静娴. 2020. 莺歌海盆地乐东地区中深层储层发育特征及成因机理. 岩性油气藏, 32(1): 19-26.
[Li W, Lu P, Ai N P, Shao Y, Hou J X. 2020. Development characteristics and genetic mechanism of med-deep reservoirs in Ledong area, Yinggehai Basin. Lithologic Reservoirs, 32(1): 19-26] [文内引用:1]
[8] 梁则亮, 毛晨飞, 肖华, 陈国军, 高衍武, 高明, 张啸. 2022. 岩石物理相约束下的砂砾岩岩性粒级精细划分: 以准噶尔盆地乌尔禾组为例. 长江大学学报(自然科学版), 19(4): 28-37.
[Liang Z L, Mao C F, Xiao H, Chen G J, Gao Y W, Gao M, Zhang X. 2022. Fine classification of lithologic grade of sand -conglomerate under the constraint of petrophysical facies: taking the Wuerhe Formation in the Junggar Basin as an example. Journal of Yangtze University(Natural Science Edition), 19(4): 28-37] [文内引用:1]
[9] 刘珊珊, 汪志明. 2022. 基于机器学习方法的多采样点储层粒度剖面预测. 石油科学通报, 7(1): 93-105.
[Liu S S, Wang Z M. 2022. Reservoir grain size profile prediction of multiple sampling points based on a machine learning method. Petroleum Science Bulletin, 7(1): 93-105] [文内引用:1]
[10] 刘为, 杨希冰, 张秀苹, 段亮, 邵远, 郝德峰. 2019. 莺歌海盆地东部黄流组重力流沉积特征及其控制因素. 岩性油气藏, 31(2): 75-82.
[Liu W, Yang X B, Zhang X P, Duan L, Shao Y, Hao D F. 2019. Characteristics and controlling factors of gravity flow deposits of Huangliu Formation in eastern Yinggehai Basin. Lithologic Reservoirs, 31(2): 75-82] [文内引用:1]
[11] 刘毅, 陆正元, 吕晶, 谢润成. 2017. 主成分分析法在泥页岩地层岩性识别中的应用. 断块油气田, 24(3): 360-363.
[Liu Y, Lu Z Y, Lü J, Xie R C. 2017. Application of principal component analysis method in lithology identification for shale formation. Fault-Block Oil & Gas Field, 24(3): 360-363] [文内引用:1]
[12] 罗利, 朱心万, 常俊, 周政英, 胡振平. 2007. 苏5、桃7区块不同粒度碎屑岩测井识别方法. 天然气工业, 27(12): 36-38.
[Luo L, Zhu X W, Chang J, Zhou Z Y, Hu Z P. 2007. Logging recognition methods for clastic rocks with different granularities in blocks SU-5 and TAO-7. Natural Gas Industry, 27(12): 36-38] [文内引用:1]
[13] 罗歆, 闫建平, 王军, 耿斌, 王敏, 钟广海, 张帆, 李志鹏, 高松洋. 2023. 基于FMI图像深度学习的砂砾岩体沉积微相识别方法: 以东营凹陷北带 Y920区块沙四上亚段为例. 沉积学报, 41(4): 1138-1152.
[Luo X, Yan J P, Wang J, Geng B, Wang M, Zhong G H, Zhang F, Li Z P, Gao S Y. 2023. A method for identifying sedimentary microfacies in a sand y conglomerate body on deep learning of FMI images: case study of upper submember of the Fourth member, Shahejie Formation in Y920 block, northern zone, Dongying Sag. Acta Sedimentologica Sinica, 41(4): 1138-1152] [文内引用:1]
[14] 马峥, 张春雷, 高世臣. 2017. 主成分分析与模糊识别在岩性识别中的应用. 岩性油气藏, 29(5): 127-133.
[Ma Z, Zhang C L, Gao S C. 2017. Lithology identification based on principal component analysis and fuzzy recognition. Lithologic Reservoirs, 29(5): 127-133] [文内引用:1]
[15] 毛倩茹, 范彩伟, 罗静兰, 曹江骏, 尤丽, 符勇, 李珊珊, 史肖凡, 吴仕玖. 2022. 超压背景下中深层砂岩储集层沉积—成岩演化差异性分析: 以南海莺歌海盆地中新统黄流组为例. 古地理学报, 24(2): 344-360.
[Mao Q R, Fan C W, Luo J L, Cao J J, You L, Fu Y, Li S S, Shi X F, Wu S J. 2022. Analysis of sedimentary-diagenetic evolution difference on middle-deep buried sand stone reservoirs under overpressure background: a case study of the Miocene Huangliu Formation in Yinggehai Basin, South China Sea. Journal of Palaeogeography(Chinese Edition), 24(2): 344-360] [文内引用:1]
[16] 任建业, 雷超. 2011. 莺歌海—琼东南盆地构造—地层格架及南海动力变形分区. 地球物理学报, 54(12): 3303-3314.
[Ren J Y, Lei C. 2011. Tectonic stratigraphic framework of Yinggehai-Qiongdongnan Basins and its implication for tectonic province division in South China Sea. Chinese Journal of Geophysics, 54(12), 3303-3314] [文内引用:1]
[17] 孙予舒, 黄芸, 梁婷, 季汉成, 向鹏飞, 徐新蓉. 2020. 基于XGBoost算法的复杂碳酸盐岩岩性测井识别. 岩性油气藏, 32(4): 98-106.
[Sun Y S, Huang Y, Liang T, Ji H C, Xiang P F, Xu X R. 2020. Identification of complex carbonate lithology by logging based on XGBoost algorithm. Lithologic Reservoirs, 32(4): 98-106] [文内引用:1]
[18] 谭增驹, 郑宏安, 张超谟, 刘子云. 1995. 利用粒度中值平均粒径研究陆源碎屑岩岩性与结构. 测井技术, 19(2): 130-134.
[Tan Z J, Zheng H A, Zhang C M, Liu Z Y. 1995. Study of the lithology and texture of terrigenous clastic rock with medium grain size and average grain diameter. Well Logging Technology, 19(2): 130-134] [文内引用:1]
[19] 田艳, 孙建孟, 王鑫, 田国栋. 2010. 利用逐步法和Fisher判别法识别储层岩性. 勘察地球物理进展, 33(2): 126-134.
[Tian Y, Sun J M, Wang X, Tian G D. 2010. Identifying reservoir lithology by step-by-step method and Fisher discriminant. Petroleum Reservoir Evaluation and Development, 33(2): 126-134] [文内引用:1]
[20] 吴进波, 张海荣, 陈现. 2022. 核磁测井资料在岩石粒度反演中的应用. 海洋石油, 42(3): 67-73.
[Wu J B, Zhang H R, Chen X. 2022. The application of NMR logging data in the inversion of rock grain size. Offshore Oil, 42(3): 67-73] [文内引用:1]
[21] 吴仕玫, 范彩伟, 招湛杰, 代龙, 邓孝亮, 钟佳. 2019. 莺歌海盆地乐东区碳酸盐胶结物成因及地质意义. 地球科学, 44(8): 2686-2694.
[Wu S M, Fan C W, Zhao Z J, Dai L, Deng X L, Zhong J. 2019. Origin of carbonate cement in reservoirs of Ledong Area, Yinggehai Basin and its geological significance. Earth Science, 44(8): 2686-2694] [文内引用:1]
[22] 谢晓庆, 吴伟, 程亮, 赵莉, 隋秀英, 刘春雷. 2022. 复杂岩性储层渗透率建模中的应用. 工程地球物理学报, 19(3): 310-315.
[Xie X Q, Wu W, Cheng L, Zhao L, Sui X Y, Liu C L. 2022. Application of granularity analysis in permeability modeling of complex lithologic reservoir. Chinese Journal of Engineering Geophysics, 19(3): 310-315] [文内引用:1]
[23] 谢玉洪. 2011. 莺歌海高温超压盆地压力预测模式及成藏新认识. 天然气工业, 31(12): 21-25.
[Xie Y H. 2011. Models of pressure prediction and new understand ings of hydrocarbon accumulation in the Yinggehai Basin with high temperature and super-high pressure. Natural Gas Industry, 31(12): 21-25] [文内引用:1]
[24] 闫建平, 蔡进功, 赵铭海, 李尊芝, 徐冠华. 2011. 电成像测井在砂砾岩体沉积特征研究中的应用. 石油勘探与开发, 38(4): 444-451.
[Yan J P, Cai J G, Zhao M H, Li Z Z, Xu G H. 2011. Application of electrical image logging in the study of sedimentary characteristics of sand y conglomerates. Petroleum Exploration and Development, 38(4): 444-451] [文内引用:1]
[25] 杨计海, 黄保家, 陈殿远. 2018. 莺歌海盆地坳陷斜坡带低孔特低渗气藏形成条件及勘探潜力. 中国海上油气, 30(1): 11-21.
[Yang J H, Huang B J, Chen D Y. 2018. Accumulation condition and exploration potential of low porosity and ultra-low permeability sand stone gas reservoirs on the depression slope belt of Yinggehai Basin. China Offshore Oil and Gas, 30(1): 11-21] [文内引用:1]
[26] 杨俊闯, 赵超. 2019. K-Means聚类算法研究综述. 计算机工程与应用, 55(23): 7-14.
[Yang J C, Zhao C. 2019. Survey on K-Means clustering algorithm. Computer Engineering and Applications, 55(23): 7-14] [文内引用:1]
[27] 杨楷乐, 何胜林, 杨朝强, 王猛, 张瑞雪, 任双坡, 赵晓博, 姚光庆. 2023. 高温—超压—高CO2背景下致密砂岩储层成岩作用特征: 以莺歌海盆地LD10区新近系梅山组—黄流组为例. 岩性油气藏, 35(1): 83-95.
[Yang K L, He S L, Yang Z Q, Wang M, Zhang R X, Ren S P, Zhao X B, Yao G Q. 2023. Diagenesis characteristics of tight sand stone reservoirs with high temperature, overpressure and high CO2 content: a case study of Neogene Meishan-Huangliu Formation in LD10 area, Yinggehai Basin. Lithologic Reservoirs, 35(1): 83-95] [文内引用:1]
[28] 杨宁, 王贵文, 赖锦, 李鉴伦, 苍丹, 蒋其君. 2012. 应用伽马测井曲线小波变换计算粒度参数. 现代地质, 26(4): 778-783.
[Yang N, Wang G W, Lai J, Li J L, Cang D, Jiang Q J. 2012. Application of gamma curves wavelet transform to calculate grain size parameters. Geoscience, 26(4): 778-783] [文内引用:1]
[29] 尤丽, 范彩伟, 吴仕玫, 罗静兰, 李才, 代龙, 李驰. 2021. 莺歌海盆地乐东区储层碳酸盐胶结物成因机理及与流体活动的关系. 地质学报, 95(2): 578-587.
[You L, Fan C W, Wu S J, Luo J L, Li C, Dai L, Li C. 2021. Genesis of carbonate cement and its relationship with fluid activity in the Ledong area, Yinggehai Basin. Acta Geologica Sinica, 95(2): 578-587] [文内引用:1]
[30] 张强, 李家金, 王毛毛, 唐湘飞. 2022. 基于改进主成分分析法的测井曲线岩性分层技术. 吉林大学学报(地球科学版), 52(4): 1369-1376.
[Zhang Q, Li J J, Wang M M, Tang X F. 2022. Logging curve rock layering technology based on improved principal component analysis. Journal of Jilin University(Earth Science Edition), 52(4): 1369-1376] [文内引用:1]
[31] 张涛, 莫修文. 2007. 基于交会图与模糊聚类算法的复杂岩性识别. 吉林大学学报(地球科学版), 37(增刊1): 109-113.
[Zhang T, Mo X W. 2007. Complex lithologic identification based on cross plot and fuzzy clustering algorithm. Journal of Jilin University(Earth Science Edition), 37(Supplement 1): 109-113] [文内引用:1]
[32] 张焱, 周永章, 朱继田. 2015. 基于主成分的多重分形法在岩性识别中的应用. 中山大学学报(自然科学版), 54(3): 145-157.
[Zhang Y, Zhou Y Z, Zhu J T. 2015. Multi-fractal method's application based on principal component in lithology recognition. Acta Scientiarum Naturalium Universitatis Sunyatseni, 54(3): 145-157] [文内引用:1]
[33] 赵军, 肖承文, 王淼, 陈伟中. 2013. 测井资料在沉积物粒序反演中的应用. 地球科学, 38(4): 792-796.
[Zhao J, Xiao C W, Wang M, Chen W Z. 2013. Application of logging data to the sediment size-grading inversion. Earth Science, 38(4): 792-796] [文内引用:1]
[34] 赵军, 代新雪, 古莉, 祁新忠, 陈伟中. 2016. 基于粒度控制的复杂储层渗透性建模方法. 吉林大学学报(地球科学版), 46(1): 279-285.
[Zhao J, Dai X X, Gu L, Qi X Z, Chen W Z. 2016. Method of permeability model establishment based on the complex reservoir controlled by particle-size. Journal of Jilin University(Earth Science Edition), 46(1): 279-285] [文内引用:1]
[35] 赵笑笑, 闫建平, 王敏, 何贤, 钟光海, 王军, 耿斌, 胡钦红, 李志鹏. 2022. 沾化凹陷沙河街组湖相泥页岩夹层特征及测井识别方法. 岩性油气藏, 34(1): 118-129.
[Zhao X X, Yan J P, Wang M, He X, Zhong G H, Wang J, Geng B, Hu Q H, Li Z P. 2022. Logging identification method of lacustrine shale interlayers of Shahejie Formation in Zhanhua Sag. Lithologic Reservoirs, 34(1): 118-129] [文内引用:1]
[36] 朱筱敏. 2008. 沉积岩石学. 北京: 石油工业出版社.
[Zhu X M. 2008. Sedimentary Petrology. Beijing: Petroleum Industry Press] [文内引用:1]
[37] Bloch S, Land er R H, Bonnell L. 2002. Anomalously high porosity and permeability in deeply buried sand stone reservoirs: origin and predictability. AAPG Bulletin, 86(2): 301-328. [文内引用:1]
[38] Chen T Q, Guestrin C. 2016. XGBoost: a scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco, California, USA: 785-794. [文内引用:1]
[39] Conroy T. 2010. Using nuclear magnetic resonance data for grain size estimation and expand able sand screen design. SPWLA 51st Annual Logging Symposium. [文内引用:1]
[40] Faga A T, Oyeneyin B M. 2000. Application of neural networks for improved gravel-pack design. SPE: 58722. [文内引用:1]
[41] Folk R L, Ward W C. 1957. Brazos River bar: a study in the significance of grain size parameters. Journal of Sedimentary Petrology, 27: 3-26. [文内引用:1]
[42] Friedman G M, Johnson K G. 1982. Exercises in Sedimentology. New York: John Wiley and Sons, 68-83. [文内引用:1]
[43] Hurst A R. 1990. Natural gamma-ray spectrometry in hydrocarbon-bearing sand stones from the Norwegian Continental Shelf. Geological Society, London, Special Publications, 48(1): 211-222. [文内引用:1]
[44] McManus J. 1988. Grain Size Determination and Interpretation. Tucker Med. Techniques in Sedimentology. Oxford: Wiley Blackwell, 63-85. [文内引用:1]
[45] Xin Y, Wang G W, Liu B C, Ai Y, Cai D Y, Yang S W, Liu H K, Xie Y Q, Chen K J. 2022. Pore structure evaluation in ultra-deep tight sand stones using NMR measurements and fractal analysis. Journal of Petroleum Science and Engineering, 211: 110-180. [文内引用:1]
[46] Yuan G H, Cao Y C, Qiu L W. 2017. Genetic mechanism of high-quality reservoirs in Permian tight fan delta conglomerates at the northwestern margin of the Junggar Basin, north western China. AAPG Bulletin, 101(12): 1995-2019. [文内引用:1]